
Question and Answers Forum
Question Number 27936 by Tinkutara last updated on 17/Jan/18
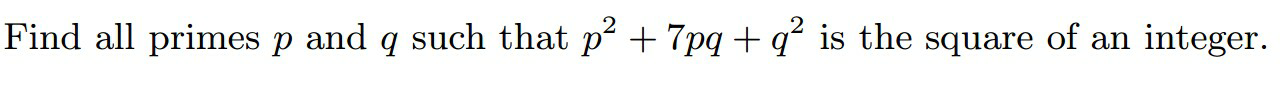
Commented by Rasheed.Sindhi last updated on 19/Jan/18

Answered by Rasheed.Sindhi last updated on 17/Jan/18

Answered by mrW2 last updated on 18/Jan/18
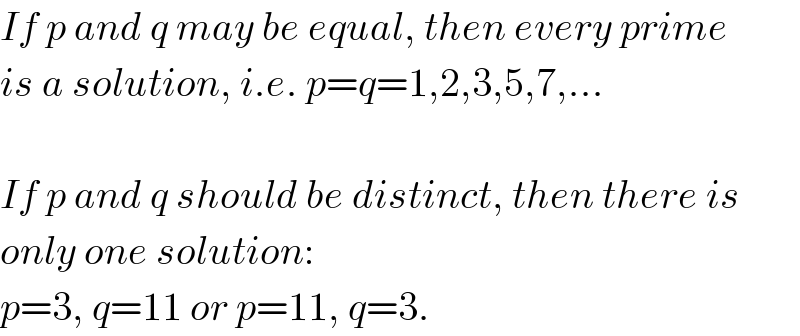
Commented by mrW2 last updated on 18/Jan/18
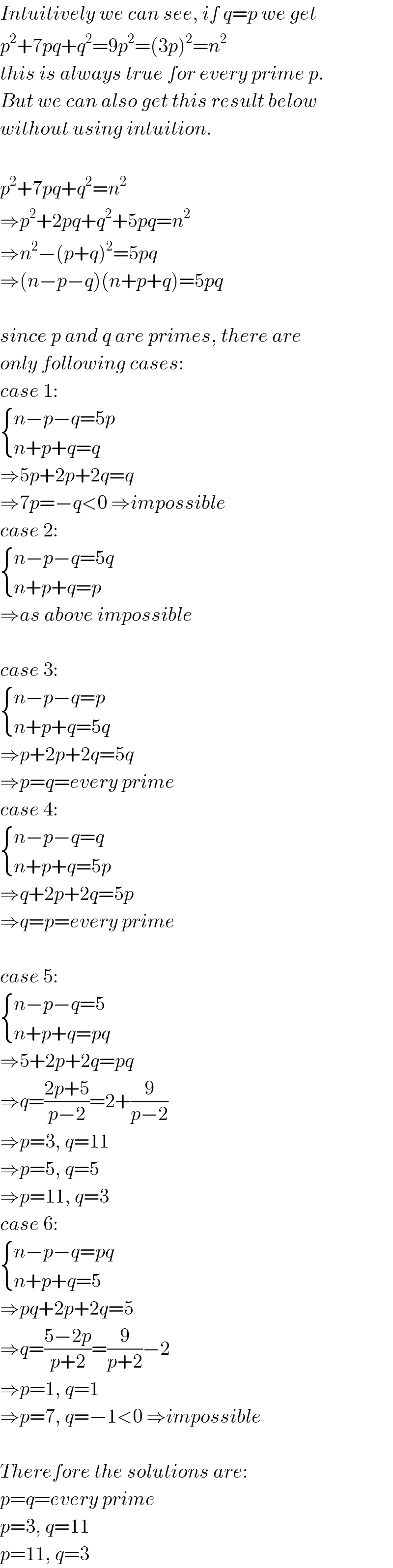
Commented by mrW2 last updated on 18/Jan/18
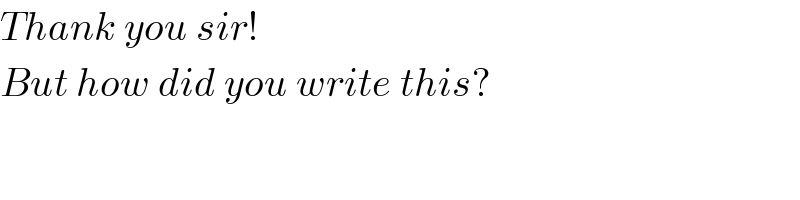
Commented by Tinkutara last updated on 18/Jan/18
ᝨℍᗅℕK ℽᝪႮ Ꮙℰℛℽ ℳႮℂℍ Տⅈℛ��! ⅈ ℊᝪᝨ ᝨℍℰ ᗅℕՏᗯℰℛ.
Commented by Rasheed.Sindhi last updated on 18/Jan/18
�������������� ������ !
Commented by Rasheed.Sindhi last updated on 18/Jan/18

Commented by mrW2 last updated on 18/Jan/18
����
