Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2796 by Rasheed Soomro last updated on 27/Nov/15

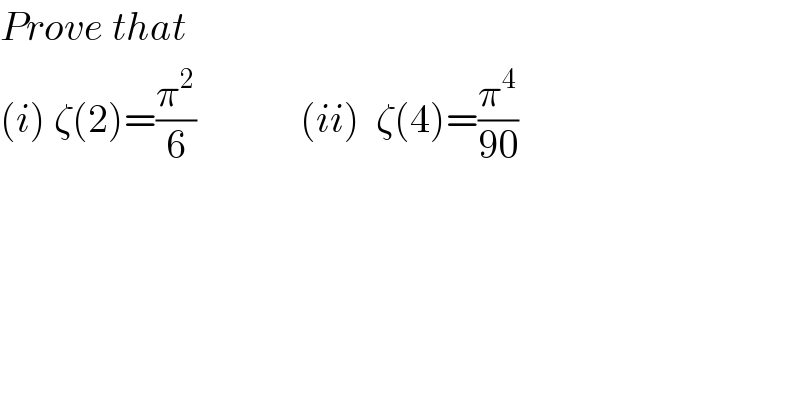
Prove that (i) ζ(2)=(π^2 /6) (ii) ζ(4)=(π^4 /(90))

$${Prove}\:{that} \\ $$$$\left({i}\right)\:\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\:\:\left({ii}\right)\:\:\zeta\left(\mathrm{4}\right)=\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$

Answered by prakash jain last updated on 28/Nov/15

(i) ζ(2)=(π^2 /6) There are several proofs available for ζ(2). I am giving a proof which utilizes some of the question already asked Q2735, Q2751 and Q2806. f(x)=Σ_(n=1) ^∞ ((cos nx)/n^2 ) is uniformly converged on R. Q2806 g(x)=Σ_(n=1) ^∞ ((sin nx)/n) is convergent on (0,2π) Q2735 Σ_(n=1) ^∞ ((sin nx)/n) = ((π−x)/2) Q2751 f ′(x)=−g(x)=((x−π)/2) ∫_0 ^π (−g(x))dx=f(π)−f(0) ∵f(x)=∫−g(x)dx ∫_0 ^π (−g(x))dx=∫_0 ^( π) ((x−π)/2)dx=−(π^2 /4) f(0)=ζ(2) f(π)=Σ_(n=1) ^∞ (((−1)^n )/n^2 )=−η(2)=−(1/2)ζ(2) η(2) is eta function −(1/2)ζ(2)−ζ(2)=−(π^2 /4) ζ(2)=(π^2 /6)

$$\left({i}\right)\:\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\mathrm{There}\:\mathrm{are}\:\mathrm{several}\:\mathrm{proofs}\:\mathrm{available}\:\mathrm{for}\:\zeta\left(\mathrm{2}\right).\:\mathrm{I} \\ $$$$\mathrm{am}\:\mathrm{giving}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{which}\:\mathrm{utilizes}\:\mathrm{some}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{already}\:\mathrm{asked}\:\mathrm{Q2735},\:\mathrm{Q2751} \\ $$$$\mathrm{and}\:\mathrm{Q2806}. \\ $$$${f}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\:{nx}}{{n}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{uniformly}\:\mathrm{converged}\:\mathrm{on}\:\mathbb{R}.\:\mathrm{Q2806} \\ $$$${g}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\:{nx}}{{n}}\:\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{on}\:\left(\mathrm{0},\mathrm{2}\pi\right)\:\:\mathrm{Q2735} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{sin}\:{nx}}{{n}}\:=\:\frac{\pi−{x}}{\mathrm{2}}\:\:\:\:\:\mathrm{Q2751} \\ $$$${f}\:'\left({x}\right)=−{g}\left({x}\right)=\frac{{x}−\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\pi} \left(−{g}\left({x}\right)\right){dx}={f}\left(\pi\right)−{f}\left(\mathrm{0}\right)\:\:\:\:\:\because{f}\left({x}\right)=\int−{g}\left({x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\pi} \left(−{g}\left({x}\right)\right){dx}=\int_{\mathrm{0}} ^{\:\pi} \frac{{x}−\pi}{\mathrm{2}}{dx}=−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\:\: \\ $$$${f}\left(\mathrm{0}\right)=\zeta\left(\mathrm{2}\right) \\ $$$${f}\left(\pi\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }=−\eta\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\eta\left(\mathrm{2}\right)\:\mathrm{is}\:\mathrm{eta}\:\mathrm{function} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)−\zeta\left(\mathrm{2}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Answered by 123456 last updated on 27/Nov/15

(ii) ζ(4) (Σ_(n=1) ^(+∞) (1/n^s ))^2 =Σ_(n=1) ^(+∞) (1/n^(2s) )+2Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (1/((nm)^s )) [ζ(s)]^2 =ζ(2s)+2Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (1/((nm)^s )) ζ(4)=[ζ(2)]^2 −2Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (1/((nm)^2 )) =[(π^2 /6)]^2 −2∙(π^4 /(120)) =(π^4 /(36))−(π^4 /(60)) =(((60−36)π^4 )/(36×60)) =((24π^4 )/(36×60)) =((6π^4 )/(18×30)) =(π^4 /(9×10)) =(π^4 /(90)) −−−−−detail in comment−−−−−

$$\left({ii}\right)\:\zeta\left(\mathrm{4}\right) \\ $$$$\left(\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} }\right)^{\mathrm{2}} =\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}{s}} }+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\:\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({nm}\right)^{{s}} } \\ $$$$\left[\zeta\left({s}\right)\right]^{\mathrm{2}} =\zeta\left(\mathrm{2}{s}\right)+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\:\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({nm}\right)^{{s}} } \\ $$$$\zeta\left(\mathrm{4}\right)=\left[\zeta\left(\mathrm{2}\right)\right]^{\mathrm{2}} −\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\:\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({nm}\right)^{\mathrm{2}} } \\ $$$$=\left[\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\right]^{\mathrm{2}} −\mathrm{2}\centerdot\frac{\pi^{\mathrm{4}} }{\mathrm{120}} \\ $$$$=\frac{\pi^{\mathrm{4}} }{\mathrm{36}}−\frac{\pi^{\mathrm{4}} }{\mathrm{60}} \\ $$$$=\frac{\left(\mathrm{60}−\mathrm{36}\right)\pi^{\mathrm{4}} }{\mathrm{36}×\mathrm{60}} \\ $$$$=\frac{\mathrm{24}\pi^{\mathrm{4}} }{\mathrm{36}×\mathrm{60}} \\ $$$$=\frac{\mathrm{6}\pi^{\mathrm{4}} }{\mathrm{18}×\mathrm{30}} \\ $$$$=\frac{\pi^{\mathrm{4}} }{\mathrm{9}×\mathrm{10}} \\ $$$$=\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$$$−−−−−\mathrm{detail}\:\mathrm{in}\:\mathrm{comment}−−−−− \\ $$

Commented by 123456 last updated on 27/Nov/15

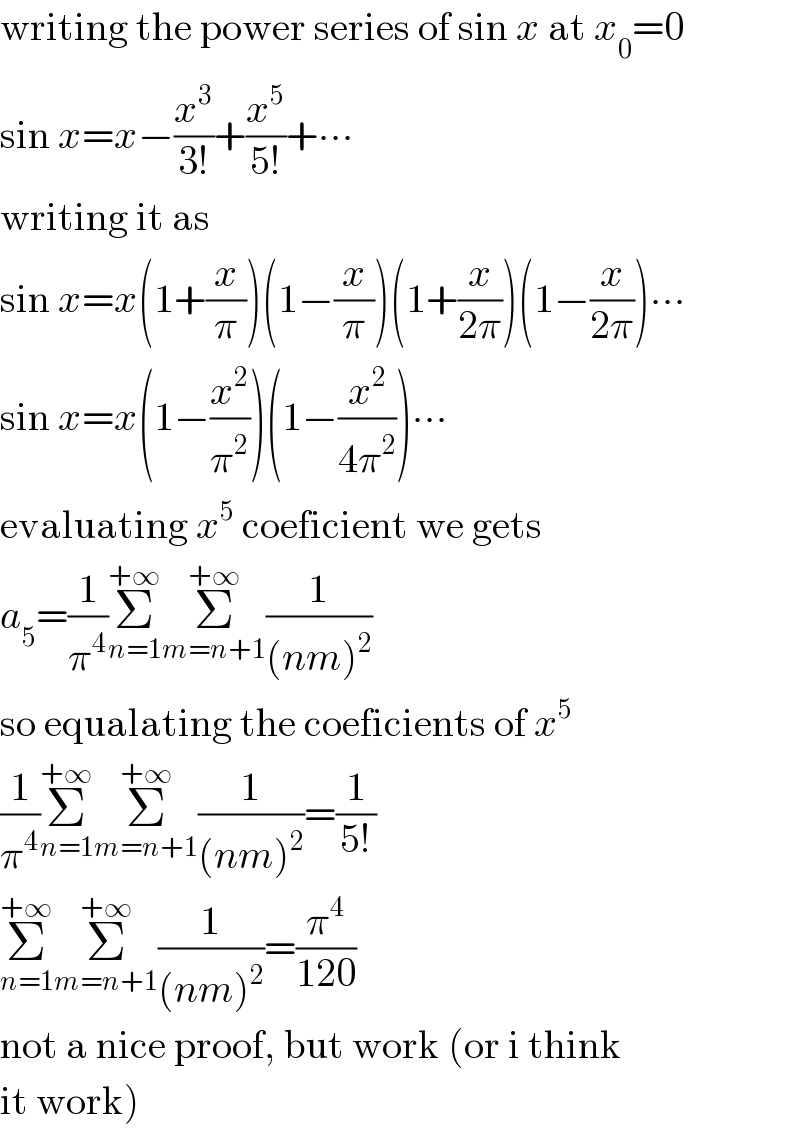
writing the power series of sin x at x_0 =0 sin x=x−(x^3 /(3!))+(x^5 /(5!))+∙∙∙ writing it as sin x=x(1+(x/π))(1−(x/π))(1+(x/(2π)))(1−(x/(2π)))∙∙∙ sin x=x(1−(x^2 /π^2 ))(1−(x^2 /(4π^2 )))∙∙∙ evaluating x^5 coeficient we gets a_5 =(1/π^4 )Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (1/((nm)^2 )) so equalating the coeficients of x^5 (1/π^4 )Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (1/((nm)^2 ))=(1/(5!)) Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (1/((nm)^2 ))=(π^4 /(120)) not a nice proof, but work (or i think it work)

$$\mathrm{writing}\:\mathrm{the}\:\mathrm{power}\:\mathrm{series}\:\mathrm{of}\:\mathrm{sin}\:{x}\:\mathrm{at}\:{x}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{sin}\:{x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}+\centerdot\centerdot\centerdot\: \\ $$$$\mathrm{writing}\:\mathrm{it}\:\mathrm{as} \\ $$$$\mathrm{sin}\:{x}={x}\left(\mathrm{1}+\frac{{x}}{\pi}\right)\left(\mathrm{1}−\frac{{x}}{\pi}\right)\left(\mathrm{1}+\frac{{x}}{\mathrm{2}\pi}\right)\left(\mathrm{1}−\frac{{x}}{\mathrm{2}\pi}\right)\centerdot\centerdot\centerdot \\ $$$$\mathrm{sin}\:{x}={x}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\pi^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}\pi^{\mathrm{2}} }\right)\centerdot\centerdot\centerdot \\ $$$$\mathrm{evaluating}\:{x}^{\mathrm{5}} \:\mathrm{coeficient}\:\mathrm{we}\:\mathrm{gets} \\ $$$${a}_{\mathrm{5}} =\frac{\mathrm{1}}{\pi^{\mathrm{4}} }\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({nm}\right)^{\mathrm{2}} } \\ $$$$\mathrm{so}\:\mathrm{equalating}\:\mathrm{the}\:\mathrm{coeficients}\:\mathrm{of}\:{x}^{\mathrm{5}} \\ $$$$\frac{\mathrm{1}}{\pi^{\mathrm{4}} }\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({nm}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{5}!} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({nm}\right)^{\mathrm{2}} }=\frac{\pi^{\mathrm{4}} }{\mathrm{120}} \\ $$$$\mathrm{not}\:\mathrm{a}\:\mathrm{nice}\:\mathrm{proof},\:\mathrm{but}\:\mathrm{work}\:\left(\mathrm{or}\:\mathrm{i}\:\mathrm{think}\right. \\ $$$$\left.\mathrm{it}\:\mathrm{work}\right) \\ $$

Commented by Rasheed Soomro last updated on 30/Nov/15

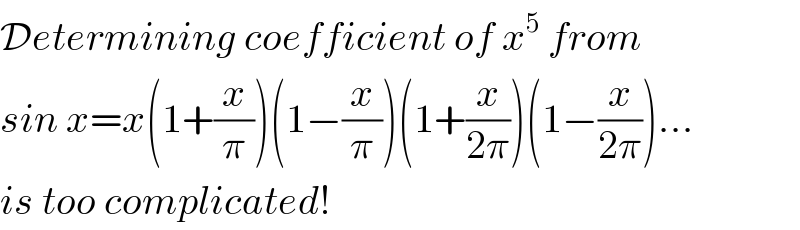
Determining coefficient of x^5 from sin x=x(1+(x/π))(1−(x/π))(1+(x/(2π)))(1−(x/(2π)))... is too complicated!

$$\mathcal{D}{etermining}\:{coefficient}\:{of}\:{x}^{\mathrm{5}} \:{from} \\ $$$${sin}\:{x}={x}\left(\mathrm{1}+\frac{{x}}{\pi}\right)\left(\mathrm{1}−\frac{{x}}{\pi}\right)\left(\mathrm{1}+\frac{{x}}{\mathrm{2}\pi}\right)\left(\mathrm{1}−\frac{{x}}{\mathrm{2}\pi}\right)... \\ $$$${is}\:{too}\:{complicated}! \\ $$

Commented by 123456 last updated on 01/Dec/15

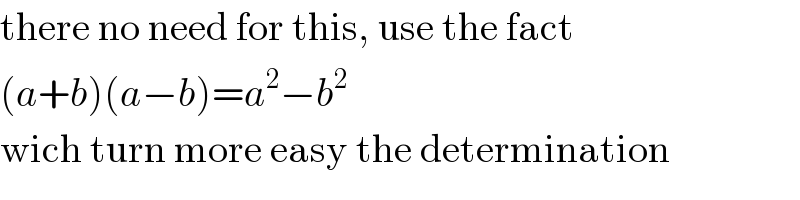
there no need for this, use the fact (a+b)(a−b)=a^2 −b^2 wich turn more easy the determination

$$\mathrm{there}\:\mathrm{no}\:\mathrm{need}\:\mathrm{for}\:\mathrm{this},\:\mathrm{use}\:\mathrm{the}\:\mathrm{fact} \\ $$$$\left({a}+{b}\right)\left({a}−{b}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\mathrm{wich}\:\mathrm{turn}\:\mathrm{more}\:\mathrm{easy}\:\mathrm{the}\:\mathrm{determination} \\ $$

Commented by Rasheed Soomro last updated on 01/Dec/15

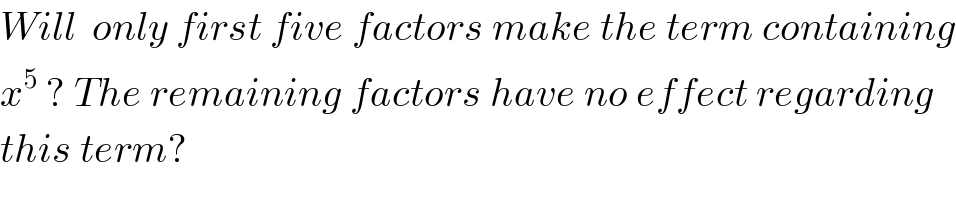
Will only first five factors make the term containing x^5 ? The remaining factors have no effect regarding this term?

$${Will}\:\:{only}\:{first}\:{five}\:{factors}\:{make}\:{the}\:{term}\:{containing} \\ $$$${x}^{\mathrm{5}} \:?\:{The}\:{remaining}\:{factors}\:{have}\:{no}\:{effect}\:{regarding} \\ $$$${this}\:{term}? \\ $$

Commented by 123456 last updated on 01/Dec/15

all terms have importance note that 5=1+2+2 so we have (only loking for the potence) 1,(0,2),(0,2),(0,2).... we have to make 5, and have to use all elements above chosing the correct from the parentys, the first choose is 1 2 2 0 0 ..... 1 2 0 2 0 ..... 1 2 0 0 2 ..... ⋮ 1 0 2 2 0 ..... 1 0 2 0 2 ..... ⋮ 1 0 0 2 2 ..... as you can see, we gets x×−(x^2 /((nπ)^2 ))×−(x^2 /((mπ)^2 )) m>n,(m,n)∈N sums all these contribuitions and them you gets Σ_(n=1) ^(+∞) Σ_(m=n+1) ^(+∞) (x^5 /((nm)^2 π^4 )) wich is you factor of x^5 similiar think hold for x,x^3 ,x^7 ,... not sure if that helped ps: making it tl x^3 is similiar to euler proof to basileia prolem the only diference is that he used ((sin x)/x) to make the manipulation (and them compared x^2 and not x^3 )

$$\mathrm{all}\:\mathrm{terms}\:\mathrm{have}\:\mathrm{importance} \\ $$$$\mathrm{note}\:\mathrm{that}\:\mathrm{5}=\mathrm{1}+\mathrm{2}+\mathrm{2} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have}\:\left(\mathrm{only}\:\mathrm{loking}\:\mathrm{for}\:\mathrm{the}\:\mathrm{potence}\right) \\ $$$$\mathrm{1},\left(\mathrm{0},\mathrm{2}\right),\left(\mathrm{0},\mathrm{2}\right),\left(\mathrm{0},\mathrm{2}\right).... \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{make}\:\mathrm{5},\:\mathrm{and}\:\mathrm{have}\:\mathrm{to}\:\mathrm{use} \\ $$$$\mathrm{all}\:\mathrm{elements}\:\mathrm{above}\:\mathrm{chosing}\:\mathrm{the}\:\mathrm{correct} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{parentys},\:\mathrm{the}\:\mathrm{first}\:\mathrm{choose}\:\mathrm{is} \\ $$$$\mathrm{1}\:\mathrm{2}\:\mathrm{2}\:\mathrm{0}\:\mathrm{0}\:..... \\ $$$$\mathrm{1}\:\mathrm{2}\:\mathrm{0}\:\mathrm{2}\:\mathrm{0}\:..... \\ $$$$\mathrm{1}\:\mathrm{2}\:\mathrm{0}\:\mathrm{0}\:\mathrm{2}\:..... \\ $$$$\vdots \\ $$$$\mathrm{1}\:\mathrm{0}\:\mathrm{2}\:\mathrm{2}\:\mathrm{0}\:..... \\ $$$$\mathrm{1}\:\mathrm{0}\:\mathrm{2}\:\mathrm{0}\:\mathrm{2}\:..... \\ $$$$\vdots \\ $$$$\mathrm{1}\:\mathrm{0}\:\mathrm{0}\:\mathrm{2}\:\mathrm{2}\:..... \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see},\:\mathrm{we}\:\mathrm{gets} \\ $$$${x}×−\frac{{x}^{\mathrm{2}} }{\left({n}\pi\right)^{\mathrm{2}} }×−\frac{{x}^{\mathrm{2}} }{\left({m}\pi\right)^{\mathrm{2}} }\:\:\:{m}>{n},\left({m},{n}\right)\in\mathbb{N} \\ $$$$\mathrm{sums}\:\mathrm{all}\:\mathrm{these}\:\mathrm{contribuitions}\:\mathrm{and}\:\mathrm{them} \\ $$$$\mathrm{you}\:\mathrm{gets} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\underset{{m}={n}+\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{x}^{\mathrm{5}} }{\left({nm}\right)^{\mathrm{2}} \pi^{\mathrm{4}} }\:\mathrm{wich}\:\mathrm{is}\:\mathrm{you}\:\mathrm{factor}\:\mathrm{of}\:{x}^{\mathrm{5}} \\ $$$$\mathrm{similiar}\:\mathrm{think}\:\mathrm{hold}\:\mathrm{for}\:{x},{x}^{\mathrm{3}} ,{x}^{\mathrm{7}} ,... \\ $$$$\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{that}\:\mathrm{helped} \\ $$$$\mathrm{ps}:\:\mathrm{making}\:\mathrm{it}\:\mathrm{tl}\:{x}^{\mathrm{3}} \:\mathrm{is}\:\mathrm{similiar}\:\mathrm{to}\:\mathrm{euler}\:\mathrm{proof}\:\mathrm{to}\:\mathrm{basileia}\:\mathrm{prolem} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{diference}\:\mathrm{is}\:\mathrm{that}\:\mathrm{he}\:\mathrm{used} \\ $$$$\frac{\mathrm{sin}\:{x}}{{x}}\:\mathrm{to}\:\mathrm{make}\:\mathrm{the}\:\mathrm{manipulation}\:\left(\mathrm{and}\:\mathrm{them}\right. \\ $$$$\left.\mathrm{compared}\:{x}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{not}\:{x}^{\mathrm{3}} \right) \\ $$

Commented by Rasheed Soomro last updated on 01/Dec/15

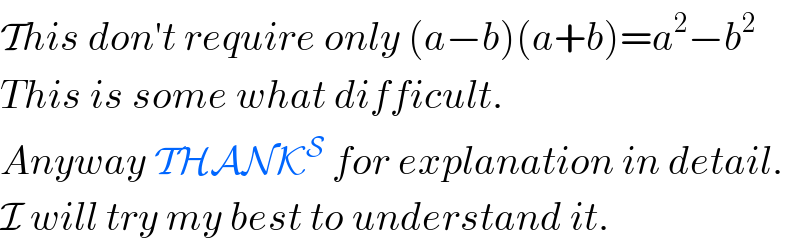
This don′t require only (a−b)(a+b)=a^2 −b^2 This is some what difficult. Anyway THANK^S for explanation in detail. I will try my best to understand it.

$$\mathcal{T}{his}\:{don}'{t}\:{require}\:{only}\:\left({a}−{b}\right)\left({a}+{b}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$${This}\:{is}\:{some}\:{what}\:{difficult}. \\ $$$${Anyway}\:\mathcal{THANK}^{\mathcal{S}} \:{for}\:{explanation}\:{in}\:{detail}. \\ $$$$\mathcal{I}\:{will}\:{try}\:{my}\:{best}\:{to}\:{understand}\:{it}. \\ $$

Commented by 123456 last updated on 02/Dec/15

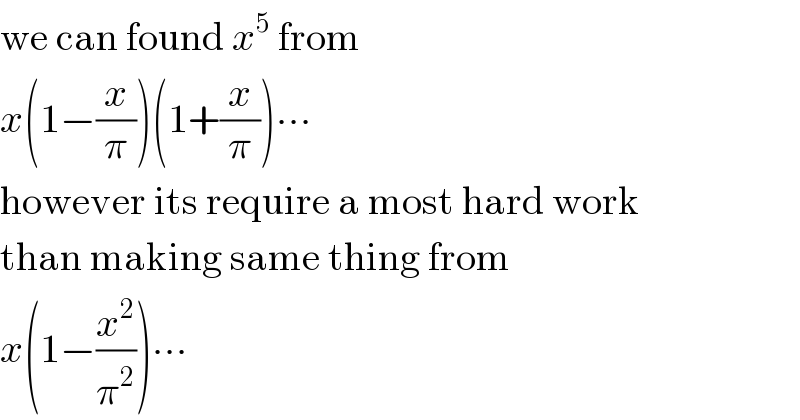
we can found x^5 from x(1−(x/π))(1+(x/π))∙∙∙ however its require a most hard work than making same thing from x(1−(x^2 /π^2 ))∙∙∙

$$\mathrm{we}\:\mathrm{can}\:\mathrm{found}\:{x}^{\mathrm{5}} \:\mathrm{from} \\ $$$${x}\left(\mathrm{1}−\frac{{x}}{\pi}\right)\left(\mathrm{1}+\frac{{x}}{\pi}\right)\centerdot\centerdot\centerdot \\ $$$$\mathrm{however}\:\mathrm{its}\:\mathrm{require}\:\mathrm{a}\:\mathrm{most}\:\mathrm{hard}\:\mathrm{work} \\ $$$$\mathrm{than}\:\mathrm{making}\:\mathrm{same}\:\mathrm{thing}\:\mathrm{from} \\ $$$${x}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\pi^{\mathrm{2}} }\right)\centerdot\centerdot\centerdot \\ $$

Commented by Rasheed Soomro last updated on 02/Dec/15

Of course sir!

$$\mathcal{O}{f}\:{course}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com