
Question and Answers Forum
Question Number 28027 by ajfour last updated on 18/Jan/18
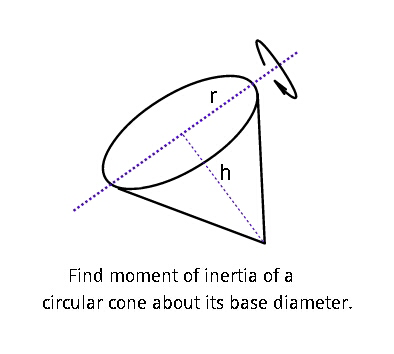
Answered by mrW2 last updated on 19/Jan/18
)^2 R^2 dx =((ρπhR^4 )/4)∫_0 ^( h) [((4h^2 )/R^2 )((x/h))^2 +(1−(x/h))^2 ](1−(x/h))^2 d((x/h)) =((ρπhR^4 )/4)∫_0 ^( 1) [((4h^2 )/R^2 )(1−s)^2 +s^2 ]s^2 ds =((ρπhR^4 )/4)∫_0 ^( 1) [((4h^2 )/R^2 )(s^2 −2s^3 +s^4 )+s^4 ]ds =((ρπhR^4 )/4)[((4h^2 )/R^2 )((s^3 /3)−(s^4 /2)+(s^5 /5))+(s^5 /5)]_0 ^1 =((ρπhR^4 )/4)[((4h^2 )/R^2 )((1/3)−(1/2)+(1/5))+(1/5)] =((ρπhR^4 )/4)(((2h^2 )/(15R^2 ))+(1/5)) =((ρπhR^2 (2h^2 +3R^2 ))/(60)) =((ρπhR^2 )/3)×(((2h^2 +3R^2 ))/(20)) ⇒I=((M(2h^2 +3R^2 ))/(20))](Q28030.png)
Commented by ajfour last updated on 19/Jan/18

| ||
Question and Answers Forum | ||
Question Number 28027 by ajfour last updated on 18/Jan/18 | ||
 | ||
Answered by mrW2 last updated on 19/Jan/18 | ||
)^2 R^2 dx =((ρπhR^4 )/4)∫_0 ^( h) [((4h^2 )/R^2 )((x/h))^2 +(1−(x/h))^2 ](1−(x/h))^2 d((x/h)) =((ρπhR^4 )/4)∫_0 ^( 1) [((4h^2 )/R^2 )(1−s)^2 +s^2 ]s^2 ds =((ρπhR^4 )/4)∫_0 ^( 1) [((4h^2 )/R^2 )(s^2 −2s^3 +s^4 )+s^4 ]ds =((ρπhR^4 )/4)[((4h^2 )/R^2 )((s^3 /3)−(s^4 /2)+(s^5 /5))+(s^5 /5)]_0 ^1 =((ρπhR^4 )/4)[((4h^2 )/R^2 )((1/3)−(1/2)+(1/5))+(1/5)] =((ρπhR^4 )/4)(((2h^2 )/(15R^2 ))+(1/5)) =((ρπhR^2 (2h^2 +3R^2 ))/(60)) =((ρπhR^2 )/3)×(((2h^2 +3R^2 ))/(20)) ⇒I=((M(2h^2 +3R^2 ))/(20))](Q28030.png) | ||
| ||
Commented by ajfour last updated on 19/Jan/18 | ||
 | ||