
Question and Answers Forum
Question Number 28035 by abdo imad last updated on 18/Jan/18
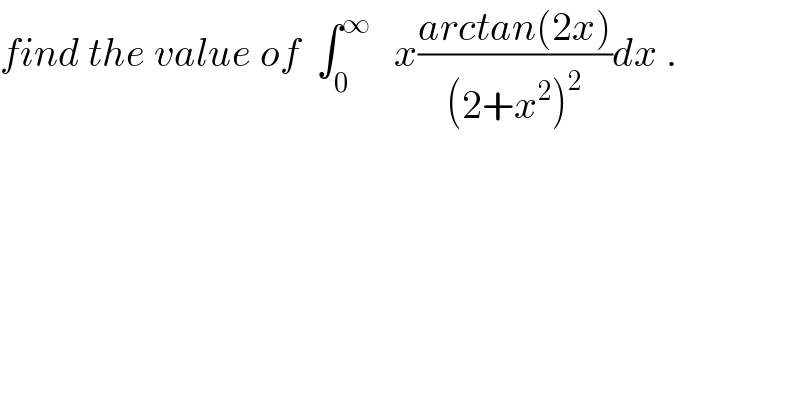
Commented by abdo imad last updated on 23/Jan/18
![let integratr by parts I= ((−1)/(2(2+x^2 ))) arctan(2x)]^(+∞) _0 +∫_0 ^∞ ((2dx)/(2(2+x^2 )(1+4x^2 ))) = ∫_0 ^∞ (dx/((2+x^2 )(1+4x^2 ))) =(1/2)∫_(R ) (dx/((2+x^2 )(1+4x^2 ))) let introduce the complex function f(z)= (1/((z^2 +2)(4z^2 +1))) poles of f? f(z)= (/(4(z−(√2)i)(x+(√2)i)(z−(i/2))(z+(i/2)))) the poles of f are (√2)i,−(√2)i,(i/2) and ((−i)/2) ∫_R f(x)dz=2iπ(Res(f,(√2)i)+Res(f,(i/2))) Res(f,(√2)i)= (1/(4(2(√2)i))(((√2)i)^2 +(1/4)))) = (1/(8(√2)i(−2 +(1/4))))= (1/(8(√2)i .((−7)/4))) = ((−1)/(14(√2)i)) Res(f,(i/2))= (1/(4((i/2) −(√2)i)((i/2)+(√2)i)i)) = (1/(4( −(1/4)+2)i))= (1/(7i)) ∫_R ^ f(z)dz=2iπ( ((−1)/(14(√2)i)) + (1/(7i))) = ((−π)/(7(√2))) +((2π)/7)=((2π(√2)−π)/(7(√2))) .](Q28269.png)
Commented by abdo imad last updated on 23/Jan/18

| ||
Question and Answers Forum | ||
Question Number 28035 by abdo imad last updated on 18/Jan/18 | ||
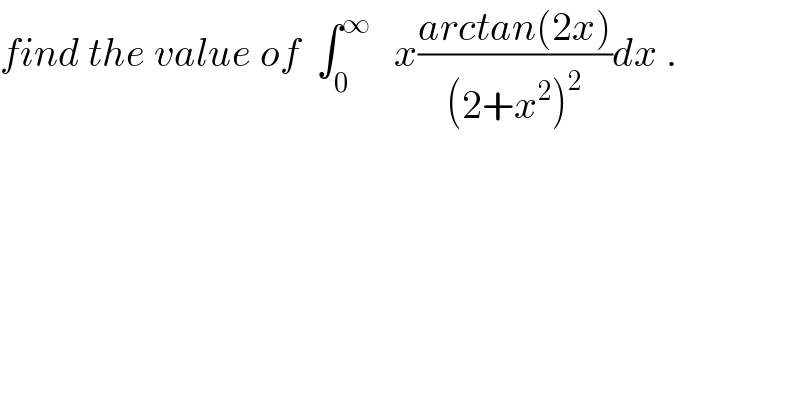 | ||
Commented by abdo imad last updated on 23/Jan/18 | ||
![let integratr by parts I= ((−1)/(2(2+x^2 ))) arctan(2x)]^(+∞) _0 +∫_0 ^∞ ((2dx)/(2(2+x^2 )(1+4x^2 ))) = ∫_0 ^∞ (dx/((2+x^2 )(1+4x^2 ))) =(1/2)∫_(R ) (dx/((2+x^2 )(1+4x^2 ))) let introduce the complex function f(z)= (1/((z^2 +2)(4z^2 +1))) poles of f? f(z)= (/(4(z−(√2)i)(x+(√2)i)(z−(i/2))(z+(i/2)))) the poles of f are (√2)i,−(√2)i,(i/2) and ((−i)/2) ∫_R f(x)dz=2iπ(Res(f,(√2)i)+Res(f,(i/2))) Res(f,(√2)i)= (1/(4(2(√2)i))(((√2)i)^2 +(1/4)))) = (1/(8(√2)i(−2 +(1/4))))= (1/(8(√2)i .((−7)/4))) = ((−1)/(14(√2)i)) Res(f,(i/2))= (1/(4((i/2) −(√2)i)((i/2)+(√2)i)i)) = (1/(4( −(1/4)+2)i))= (1/(7i)) ∫_R ^ f(z)dz=2iπ( ((−1)/(14(√2)i)) + (1/(7i))) = ((−π)/(7(√2))) +((2π)/7)=((2π(√2)−π)/(7(√2))) .](Q28269.png) | ||
Commented by abdo imad last updated on 23/Jan/18 | ||
 | ||