
Question and Answers Forum
Question Number 28073 by abdo imad last updated on 20/Jan/18
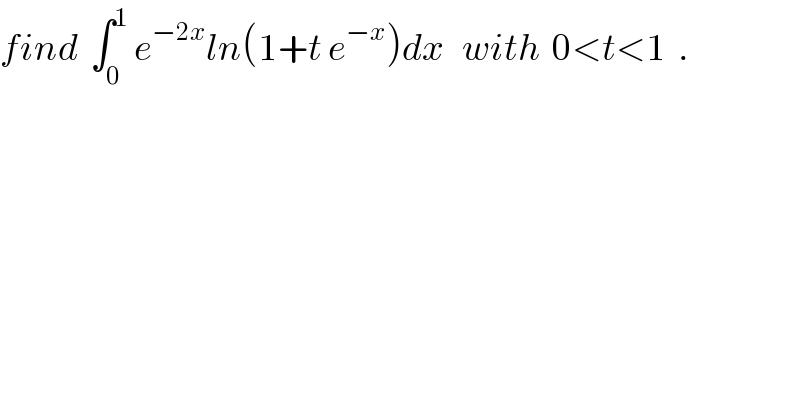
Commented byabdo imad last updated on 26/Jan/18
![let put f(t) = ∫_0 ^1 e^(−2x) ln(1+t e^(−x) )dx f^′ (t)= ∫_0 ^1 e^(−2x) (e^(−x) /(1+t e^(−x) ))dx = ∫_0 ^1 e^(−3x) (Σ_(n=0) ^∝ (−1)^n t^n e^(−nx) )dx = Σ_(n=0) ^∝ (−1)^n t^n ∫_0 ^1 e^(−(n+3)x) dx = Σ_(n=0) ^∞ (((−1)^n t^n )/(−(n+3))) [ e^(−(n+3)x) ]_0 ^1 =−Σ_(n=0) ^∞ (((−1)^n t^n )/(n+3)) (e^(−(n+3)) −1) = Σ_(n=0) ^(+∞) (((−1)^n )/(n+3)) t^n − Σ_(n=0) ^(+∞) (((−1)^n t^n e^(−(n+3)) )/(n+3)) ⇒ f(t) = ∫_0 ^t (....)du +λ = Σ_(n=0) ^∝ (((−1)^n )/((n+1)(n+3))) t^(n+1) −Σ_(n.0) ^∝ (((−1)^n t^(n+1) e^(−(n+3)) )/((n+1)(n+3))) +λ λ=f(0)=0 and f(x)= (1/2) Σ_(n=0) ^∝ (−1)^n ( (1/(n+1)) −(1/(n+3)))t^(n+1) − (e^(−2) /2)Σ_(n=0) ^∝ (−1)^n ( (1/(n+1)) − (1/(n+3)))(te^(−1) )^(n+1) = (1/(2 ))Σ_(n=0) ^∝ (((−1)^n )/(n+1))t^(n+1) −(1/2) Σ_(n=0) ^∝ (((−1)^n t^(n+1) )/(n+3)) −(e^(−2) /2) Σ_(n=0) ^∝ (((−1)^n (te^(−1) )^(n+1) )/(n+1)) +(e^(−2) /2) Σ_(n=0) ^∝ (((−1)^n (t e^(−1) )^(n+1) )/(n+3)) and all those sum are calculable ...be contiued.](Q28476.png)
| ||
Question and Answers Forum | ||
Question Number 28073 by abdo imad last updated on 20/Jan/18 | ||
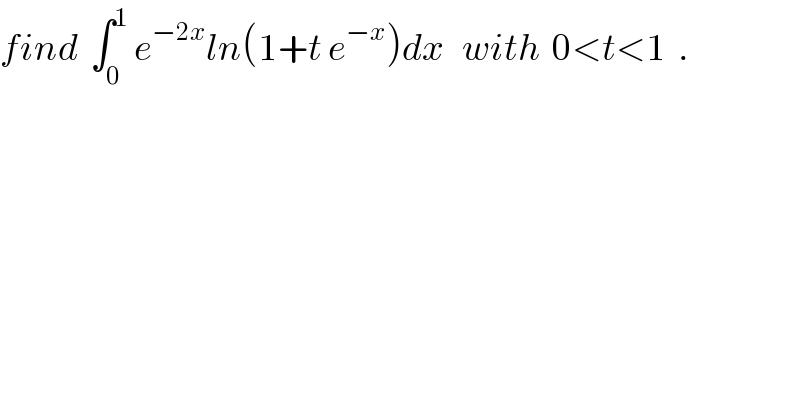 | ||
Commented byabdo imad last updated on 26/Jan/18 | ||
![let put f(t) = ∫_0 ^1 e^(−2x) ln(1+t e^(−x) )dx f^′ (t)= ∫_0 ^1 e^(−2x) (e^(−x) /(1+t e^(−x) ))dx = ∫_0 ^1 e^(−3x) (Σ_(n=0) ^∝ (−1)^n t^n e^(−nx) )dx = Σ_(n=0) ^∝ (−1)^n t^n ∫_0 ^1 e^(−(n+3)x) dx = Σ_(n=0) ^∞ (((−1)^n t^n )/(−(n+3))) [ e^(−(n+3)x) ]_0 ^1 =−Σ_(n=0) ^∞ (((−1)^n t^n )/(n+3)) (e^(−(n+3)) −1) = Σ_(n=0) ^(+∞) (((−1)^n )/(n+3)) t^n − Σ_(n=0) ^(+∞) (((−1)^n t^n e^(−(n+3)) )/(n+3)) ⇒ f(t) = ∫_0 ^t (....)du +λ = Σ_(n=0) ^∝ (((−1)^n )/((n+1)(n+3))) t^(n+1) −Σ_(n.0) ^∝ (((−1)^n t^(n+1) e^(−(n+3)) )/((n+1)(n+3))) +λ λ=f(0)=0 and f(x)= (1/2) Σ_(n=0) ^∝ (−1)^n ( (1/(n+1)) −(1/(n+3)))t^(n+1) − (e^(−2) /2)Σ_(n=0) ^∝ (−1)^n ( (1/(n+1)) − (1/(n+3)))(te^(−1) )^(n+1) = (1/(2 ))Σ_(n=0) ^∝ (((−1)^n )/(n+1))t^(n+1) −(1/2) Σ_(n=0) ^∝ (((−1)^n t^(n+1) )/(n+3)) −(e^(−2) /2) Σ_(n=0) ^∝ (((−1)^n (te^(−1) )^(n+1) )/(n+1)) +(e^(−2) /2) Σ_(n=0) ^∝ (((−1)^n (t e^(−1) )^(n+1) )/(n+3)) and all those sum are calculable ...be contiued.](Q28476.png) | ||