
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 28138 by abdo imad last updated on 21/Jan/18
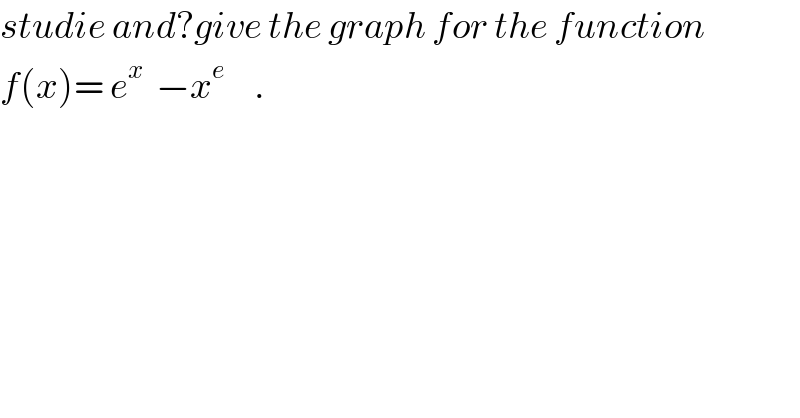
Commented by abdo imad last updated on 26/Jan/18
![we have f(x)= e^x −e^(elnx) ⇒ D_f =]0,+∝[ lim_(x→0^+ ) f(x)= 1 and lim_(x→+∞) f(x)=lim_(x→+∞) e^x ( 1−e^(−x+elnx) ) =lim_(x→+∞) e^x (1 −e^(−x(1−((elnx)/x))) )=lim _(x→+∞^ ) e^x =+∞ lim_(x→+∞) ((f(x))/x)= lim_(x→+∞) (e^x /x) − x^(e−1) =lim_(x→+∞) (e^x /x)( 1− e^(−x) x^e )=lim_(x→+∞) (e^x /x) =+∞ so the graph of f have a parabolic diction at +∞ f^′ (x)= e^x − e x^(e−1) = e^x (1− e^(−x+1) e^((e−1)lnx) ) = e^x ( 1−e^(−x+1 +(e−1)lnx) ) the sine off^′ (x) is thesine of ψ(x)= 1− e^((e−1)lnx −x+1) ψ^′ (x)= −( ((e−1)/x) −1) e^((...)) =−( ((e−1−x)/x))e^((...)) =((x−(e−1))/x) e^((...)) and ψ^′ (x)=0 ⇔ x=e−1 and f^′ (e−1)=e^(e−1) (1− e^(−e+2) e^((e−1)ln(e−1)) ).....](Q28472.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 28138 by abdo imad last updated on 21/Jan/18 | ||
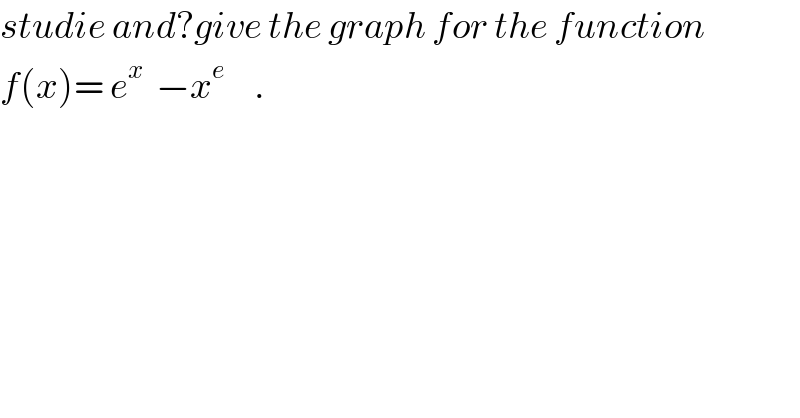 | ||
Commented by abdo imad last updated on 26/Jan/18 | ||
![we have f(x)= e^x −e^(elnx) ⇒ D_f =]0,+∝[ lim_(x→0^+ ) f(x)= 1 and lim_(x→+∞) f(x)=lim_(x→+∞) e^x ( 1−e^(−x+elnx) ) =lim_(x→+∞) e^x (1 −e^(−x(1−((elnx)/x))) )=lim _(x→+∞^ ) e^x =+∞ lim_(x→+∞) ((f(x))/x)= lim_(x→+∞) (e^x /x) − x^(e−1) =lim_(x→+∞) (e^x /x)( 1− e^(−x) x^e )=lim_(x→+∞) (e^x /x) =+∞ so the graph of f have a parabolic diction at +∞ f^′ (x)= e^x − e x^(e−1) = e^x (1− e^(−x+1) e^((e−1)lnx) ) = e^x ( 1−e^(−x+1 +(e−1)lnx) ) the sine off^′ (x) is thesine of ψ(x)= 1− e^((e−1)lnx −x+1) ψ^′ (x)= −( ((e−1)/x) −1) e^((...)) =−( ((e−1−x)/x))e^((...)) =((x−(e−1))/x) e^((...)) and ψ^′ (x)=0 ⇔ x=e−1 and f^′ (e−1)=e^(e−1) (1− e^(−e+2) e^((e−1)ln(e−1)) ).....](Q28472.png) | ||