
Question and Answers Forum
Question Number 28160 by abdo imad last updated on 21/Jan/18
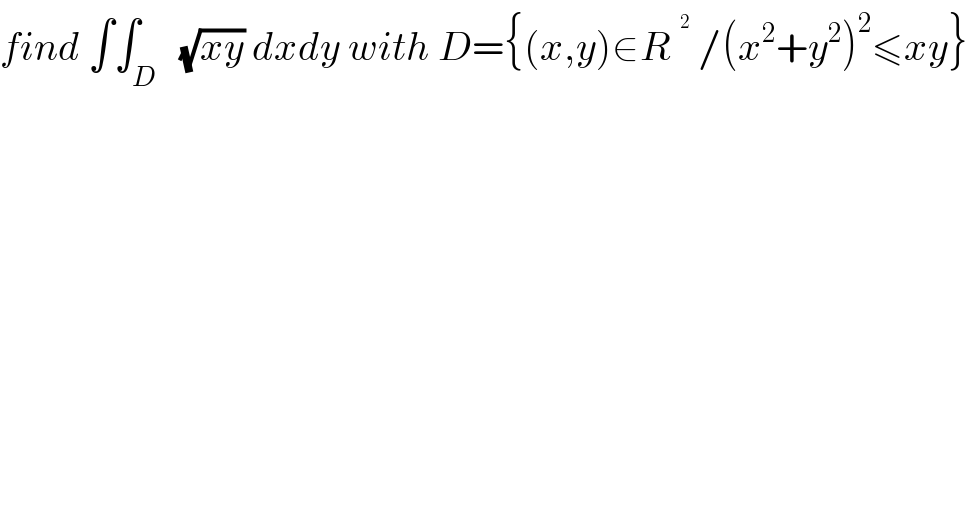
Commented by abdo imad last updated on 26/Jan/18
![let put I= ∫∫_D (√(xy)) dxdy let use he ch. x=rcosθ and y= rsinθ ⇒ 0<r^4 < r^2 cosθ sinθ ⇒0 <r^2 < (1/2)sin(2θ) so we must have sin(2θ) >0 ⇒ 0<θ< (π/2) and 0<r< (1/(√2))(√(sin(2θ))) I = ∫_0 ^(π/2) ( ∫_0 ^((1/(√2))(√(sin(2θ)))) (√(r^2 sinθ cosθ)) rdr)dθ =(1/(√2))∫_0 ^(π/2) ( ∫_0 ^((1/(√2))(√(sin(2θ)))) r^2 dr)(√(sin(2θ))) dθ =(1/(3(√2))) ∫_0 ^(π/2) [ r^3 ]_0 ^((1/(√2))(√(sin(2θ)))) (√(sin(2θ)))dθ =(1/(3(√2))) ∫_0 ^(π/2) ((1/2) sin(2θ)(1/(√2))(√(sin(2θ))) )(√(sin(2θ))))dθ = (1/(12)) ∫_0 ^(π/2) sin^2 (2θ)dθ=(1/(12)) ∫_0 ^(π/2) ((1−cos(4θ))/2)dθ](Q28452.png)
Commented by abdo imad last updated on 26/Jan/18
![I= (π/(48)) −(1/(24)) ∫_0 ^(π/2) cos(4θ)dθ= (π/(48)) − (1/(4×24))[sin(4θ)]_0 ^(π/2) =(π/(48)) −0 ⇒ I= (π/(48)) .](Q28453.png)
| ||
Question and Answers Forum | ||
Question Number 28160 by abdo imad last updated on 21/Jan/18 | ||
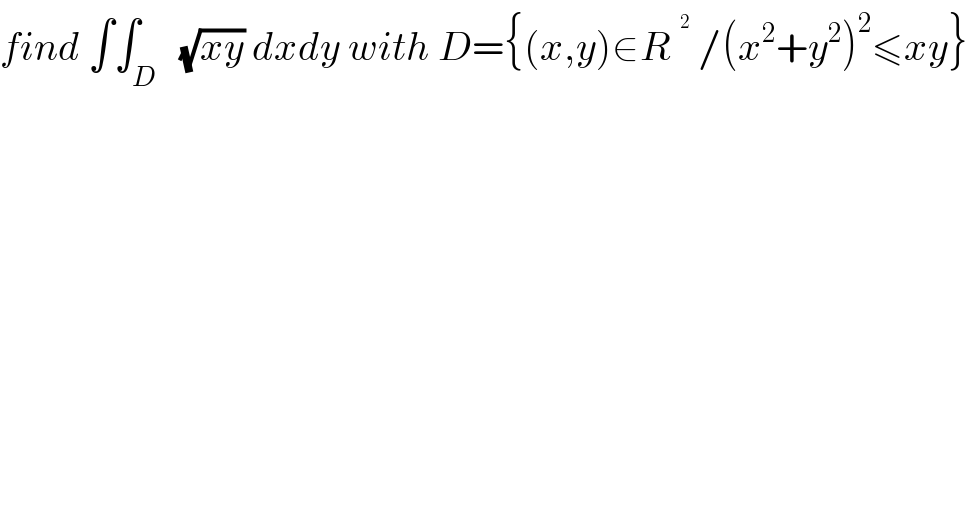 | ||
Commented by abdo imad last updated on 26/Jan/18 | ||
![let put I= ∫∫_D (√(xy)) dxdy let use he ch. x=rcosθ and y= rsinθ ⇒ 0<r^4 < r^2 cosθ sinθ ⇒0 <r^2 < (1/2)sin(2θ) so we must have sin(2θ) >0 ⇒ 0<θ< (π/2) and 0<r< (1/(√2))(√(sin(2θ))) I = ∫_0 ^(π/2) ( ∫_0 ^((1/(√2))(√(sin(2θ)))) (√(r^2 sinθ cosθ)) rdr)dθ =(1/(√2))∫_0 ^(π/2) ( ∫_0 ^((1/(√2))(√(sin(2θ)))) r^2 dr)(√(sin(2θ))) dθ =(1/(3(√2))) ∫_0 ^(π/2) [ r^3 ]_0 ^((1/(√2))(√(sin(2θ)))) (√(sin(2θ)))dθ =(1/(3(√2))) ∫_0 ^(π/2) ((1/2) sin(2θ)(1/(√2))(√(sin(2θ))) )(√(sin(2θ))))dθ = (1/(12)) ∫_0 ^(π/2) sin^2 (2θ)dθ=(1/(12)) ∫_0 ^(π/2) ((1−cos(4θ))/2)dθ](Q28452.png) | ||
Commented by abdo imad last updated on 26/Jan/18 | ||
![I= (π/(48)) −(1/(24)) ∫_0 ^(π/2) cos(4θ)dθ= (π/(48)) − (1/(4×24))[sin(4θ)]_0 ^(π/2) =(π/(48)) −0 ⇒ I= (π/(48)) .](Q28453.png) | ||