
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 28169 by abdo imad last updated on 21/Jan/18
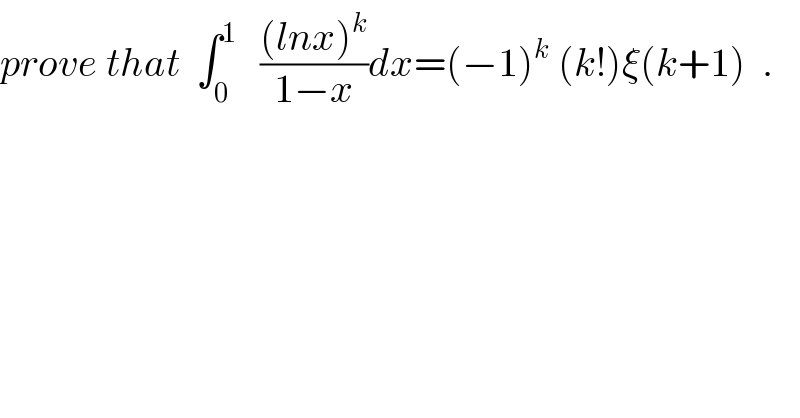
Commented by abdo imad last updated on 23/Jan/18
![we have ∫_0 ^1 (((ln(x))^k )/(1−x))dx= ∫_0 ^1 (lnx)^k (Σ_(p=0) ^(+∞) x^p )dx = Σ_(p=0) ^(+∞) ∫_0 ^1 x^p (lnx)^k dx let put I_(p,k) =∫_0 ^1 x^p (lnx)^k dx by parts we get I_(p,k) = [ (1/(p+1)) x^(p+1) (lnx)^k ]_0 ^1 − ∫_0 ^1 (1/(p+1)) x^(p+1) (k/x) (lnx)^(k−1) dx =((−k)/(p+1)) ∫_0 ^1 x^p (lnx)^(k−1) dx= ((−k)/(p+1)) I_(p,k−1 ) =(((−1)^2 k(k−1))/((p+1)^2 )) I_(p,k−2) =(((−1)^k k!)/((p+1)^k )) I_(p,0) =(((−1)^k k!)/((p+1)^(k+1) )) so ∫_0 ^1 (((lnx)^k )/(1−x))dx = Σ_(p=0) ^(+∞) (((−1)^k k!)/((p+1)^(k+1) )) = (−1)^k k! Σ_(p=0) ^(+∞) (1/((p+1)^(k+1) )) =(−1)^k k! Σ_(p=1) ^(+∞) (1/p^(k+1) )= (−1)^k k! ξ(k+1) .](Q28287.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 28169 by abdo imad last updated on 21/Jan/18 | ||
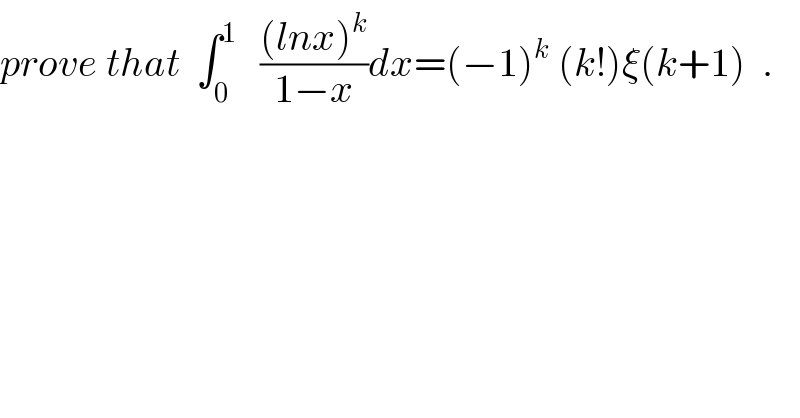 | ||
Commented by abdo imad last updated on 23/Jan/18 | ||
![we have ∫_0 ^1 (((ln(x))^k )/(1−x))dx= ∫_0 ^1 (lnx)^k (Σ_(p=0) ^(+∞) x^p )dx = Σ_(p=0) ^(+∞) ∫_0 ^1 x^p (lnx)^k dx let put I_(p,k) =∫_0 ^1 x^p (lnx)^k dx by parts we get I_(p,k) = [ (1/(p+1)) x^(p+1) (lnx)^k ]_0 ^1 − ∫_0 ^1 (1/(p+1)) x^(p+1) (k/x) (lnx)^(k−1) dx =((−k)/(p+1)) ∫_0 ^1 x^p (lnx)^(k−1) dx= ((−k)/(p+1)) I_(p,k−1 ) =(((−1)^2 k(k−1))/((p+1)^2 )) I_(p,k−2) =(((−1)^k k!)/((p+1)^k )) I_(p,0) =(((−1)^k k!)/((p+1)^(k+1) )) so ∫_0 ^1 (((lnx)^k )/(1−x))dx = Σ_(p=0) ^(+∞) (((−1)^k k!)/((p+1)^(k+1) )) = (−1)^k k! Σ_(p=0) ^(+∞) (1/((p+1)^(k+1) )) =(−1)^k k! Σ_(p=1) ^(+∞) (1/p^(k+1) )= (−1)^k k! ξ(k+1) .](Q28287.png) | ||