Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 28190 by ajfour last updated on 21/Jan/18

Commented by ajfour last updated on 21/Jan/18

$Q . 28188 (s o l u t i o n)$ $f i n d l e a s t v a l u e o f [∣ z_{1} + z_{2} ∣] + 1$ $i f z_{1}, z_{2}, z_{3}, z_{4} a r e r o o t s o f$ $z^{4} + z^{3} + z^{2} + z + 1 = 0 .$
Commented by abdo imad last updated on 21/Jan/18

$e) \Leftrightarrow z^{5} = 1 a n d z \neq 1 t h e r o o t s o f t h e p o l y n o m i a l z^{5} - 1 = 0$ $a r e z_{k} = e^{i \frac{2 k π}{5}} w i t h k \in [[1, 4]] i f w e t a k e z_{1} = e^{i \frac{2 π}{5}} a n d$ $z_{2} =^{} e^{i \frac{4 π}{5}} w e h a v e z_{2} = e^{i (π - \frac{π}{5})} = - z_{1}^{-} \Rightarrow z_{1} + z_{2} = 2 i I m (z_{1})$ $= 2 i s i n (\frac{2 π}{5}) a n d ∣ z_{1} + z_{2} ∣= 2 s i n (2 \frac{π}{5}) a n d$ $[∣ z_{1} + z_{2} ∣] + 1 = [2 s i n (\frac{2 π}{5)})] + 1 b u t w e k n o w t h a t$ $c o s (\frac{π}{5}) = \frac{1 + \sqrt{5}}{4} \Rightarrow s i n (\frac{π}{5}) = \sqrt{1 - \frac{(1 + \sqrt{{5)}^{2}}}{16}}$ $= \frac{\sqrt{16 - (6 + 2 \sqrt{5})}}{4} = \frac{\sqrt{10 - 2 \sqrt{5}}}{4} a n d$ $s i n (\frac{2 π}{5}) = 2 s i n (\frac{π}{5}) c o s (\frac{π}{5}) = 2 \frac{\sqrt{10 - 2 \sqrt{5}}}{4} \frac{1 + \sqrt{5}}{4}$ $= \frac{(1 + \sqrt{5)} \sqrt{10 - 2 \sqrt{5}}}{8} \Rightarrow 2 s i n (\frac{2 π}{5}) = \frac{(1 + \sqrt{5}) \sqrt{10 - 2 \sqrt{5}}}{4}$ $= \frac{\sqrt{(6 + 2 \sqrt{5}) (10 - 2 \sqrt{5})}}{4} = \frac{\sqrt{60 - 12 \sqrt{5} + 20 \sqrt{5} - 20}}{4}$ $= \frac{\sqrt{40 + 8 \sqrt{5}}}{4} = \frac{\sqrt{10 + 2 \sqrt{5}}}{2} = \sqrt{\frac{5}{2} + \frac{\sqrt{5}}{2}} = \sqrt{\frac{5 + \sqrt{5}}{2}} \sim \sqrt{3, 5} b u t$ $w e h a v e 1 < \sqrt{3, 5} < 2 \Rightarrow [\sqrt{3, 5}] = 1 s o$ $[∣ z_{1} + z_{2} ∣] + 1 = 2 .$
	Answered by ajfour last updated on 21/Jan/18

	$\frac{1 - z^{5}}{1 - z} = 0$ $s o z_{1}, z_{2}, z_{3}, z_{4}, 1 a r e r o o t s o f$ $z^{5} = 1 (f i f t h r o o t s o f u n i t y)$ $L e a s t v a l u e o f ∣ z_{1} + z_{2} ∣= 2 \cos 72 °$ $= 2 \sin 18 ° < 2 \sin 30 ° (= 1)$ $S o l e a s t v a l u e o f [∣ z_{1} + z_{2} ∣] + 1 = 1 .$
	Commented by ajfour last updated on 24/Jan/18

	$G e r m a n o r I n d i a n S i r ?$
	Commented by math solver last updated on 24/Jan/18

	$t h a n k y o u s o m u c h s i r!$
	Commented by math solver last updated on 22/Jan/18

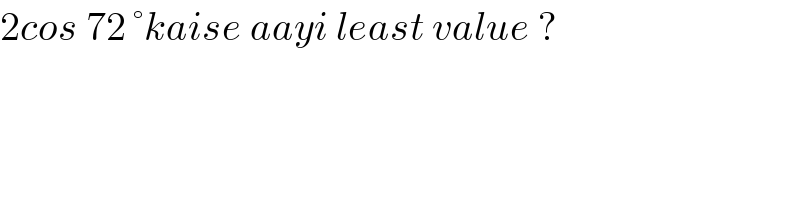
	$2 c o s 72 ° k a i s e a a y i l e a s t v a l u e ?$
	Commented by ajfour last updated on 22/Jan/18

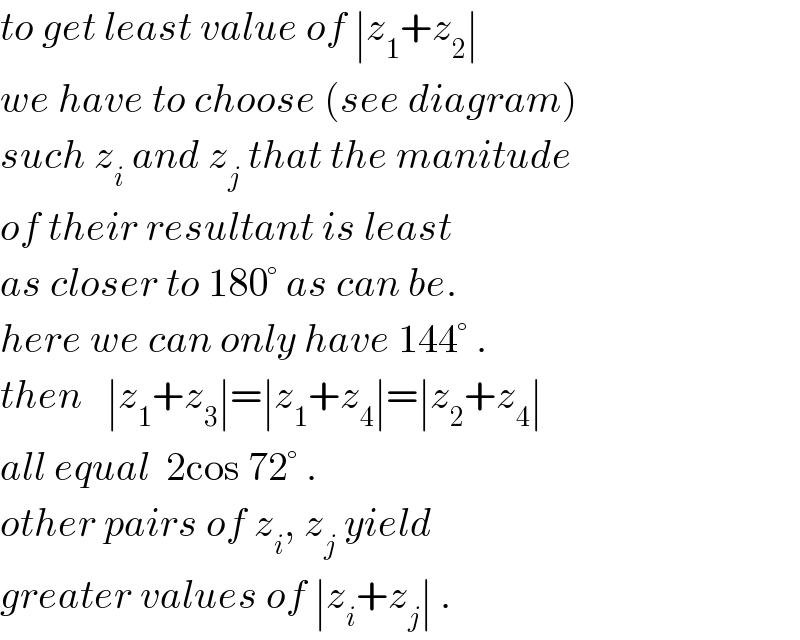
	$t o g e t l e a s t v a l u e o f ∣ z_{1} + z_{2} ∣$ $w e h a v e t o c h o o s e (s e e d i a g r a m)$ $s u c h z_{i} a n d z_{j} t h a t t h e m a n i t u d e$ $o f t h e i r r e s u l t a n t i s l e a s t$ $a s c l o s e r t o 180 ° a s c a n b e .$ $h e r e w e c a n o n l y h a v e 144 ° .$ $t h e n ∣ z_{1} + z_{3} ∣=∣ z_{1} + z_{4} ∣=∣ z_{2} + z_{4} ∣$ $a l l e q u a l 2 \cos 72 ° .$ $o t h e r p a i r s o f z_{i}, z_{j} y i e l d$ $g r e a t e r v a l u e s o f ∣ z_{i} + z_{j} ∣ .$
	Commented by math solver last updated on 22/Jan/18

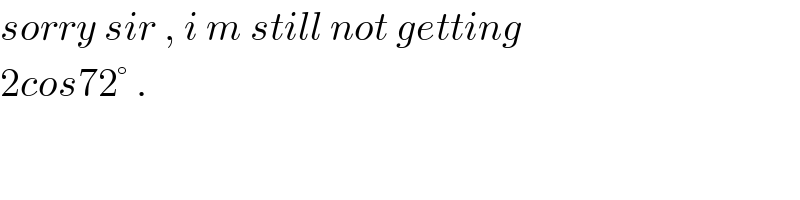
	$s o r r y s i r, i m s t i l l n o t g e t t i n g$ $2 c o s 72 ° .$
	Commented by mrW2 last updated on 23/Jan/18

	Commented by math solver last updated on 24/Jan/18

	$h e y, r u m r w 1 s i r ?$ $t h e o n e f r o m g e r m a n y .$
	Commented by mrW2 last updated on 24/Jan/18

	$y e s s i r .$ $m r W 2 = m r W 1 = m r W$
	Commented by mrW2 last updated on 24/Jan/18

	$I^{'} m f r o m G e r m a n y S i r .$
	Commented by ajfour last updated on 24/Jan/18

	$N i c e t o c o n f i r m S i r . I h a d l i k e d$ $F r a n z {K a f k a}^{'} s w o r k s S i r .$ $e s p e c i a l l y^{'} T h e {C a s t l e}^{'} .$
	Commented by mrW2 last updated on 24/Jan/18

	$N i c e t o k n o w t h a t S i r .$
	Commented by abdo imad last updated on 25/Jan/18

	$a r e y o u i n d i a n s i r a j f o u r ? m e i a m f r o m m o r o c c o . . .$
	Commented by math solver last updated on 25/Jan/18

	$y e s, h e i s f r o m i n d i a .$ $P . S : i a m a l s o a n i n d i a n :)$
	Commented by ajfour last updated on 25/Jan/18

	$n e v e r o u t s i d e I n d i a (p h y s i c a l l y) .$
	Commented by abdo imad last updated on 25/Jan/18

	$n i c e t o k n o w y o u a j f o u r, p . s . p r a k a s h j a i n . m r w . . . . w i s h y o u$ $y o u g o o d l u c k . . . .$
	Commented by mrW2 last updated on 25/Jan/18

	$T h a n k s S i r!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum