Question and Answers Forum
Question Number 28241 by ajfour last updated on 22/Jan/18

Commented by ajfour last updated on 22/Jan/18
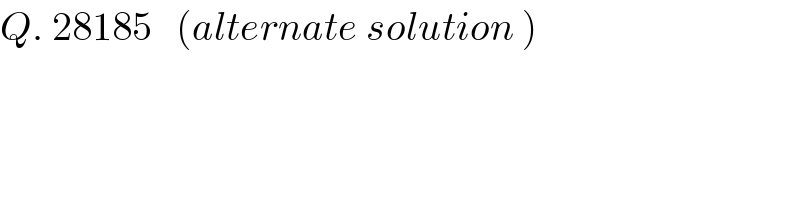
Answered by ajfour last updated on 22/Jan/18

Commented by ajfour last updated on 22/Jan/18

Commented by mrW2 last updated on 22/Jan/18
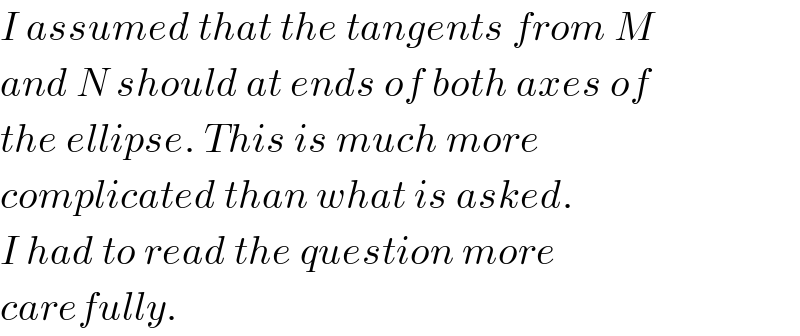
Commented by ajfour last updated on 22/Jan/18

Commented by mrW2 last updated on 23/Jan/18
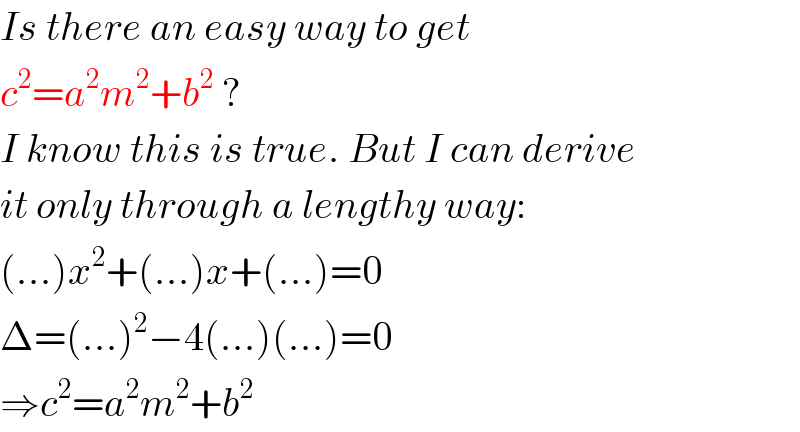
Commented by mrW2 last updated on 23/Jan/18