
Question and Answers Forum
Question Number 28268 by abdo imad last updated on 22/Jan/18
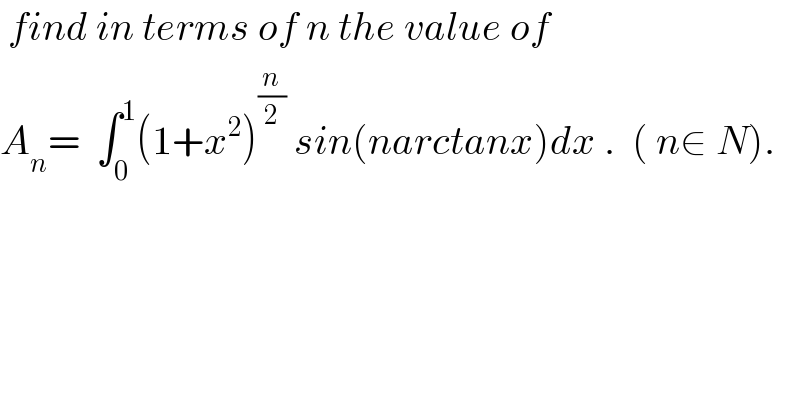
Commented by abdo imad last updated on 23/Jan/18
![let introduce the polynome P(x)= (1/(2i)) ((1+ix)^n −(1−ix)^n ) let write P(x) in geometric form .we have ∣1+ix∣= (√(1+x^2 ))= (1+x^2 )^(1/2) and 1+ix = (√(1+x^2 )) ( (1/(√(1+x^2 ))) +i(x/(√(1+x^2 ))))= r e^(iθ) ⇒ r=(√(1+x^2 )) and tanθ=x⇒ θ=artanx so (1+ix)^n = (1+x^2 )^(n/2) e^(inarctanx) (1−ix)^n =(1+x^2 )^(n/2) e^(−inartanx) and P(x)=(1/(2i))( 2iIm((1+ix)^n ))= (1+x^2 )^(n/2) sin(narctanx) ⇒ A_n =∫_0 ^1 P(x)dx but we have proved that P(x)= Σ_(p=0) ^([((n−1)/2)]) (−1)^p C_n ^(2p+1) x^(2p+1) ∫_0 ^1 P(x)dx = Σ_(p=0) ^([((n−1)/2)]) (−1)^p (C_n ^(2p+1) /(2p+2)) = A_n .](Q28282.png)
| ||
Question and Answers Forum | ||
Question Number 28268 by abdo imad last updated on 22/Jan/18 | ||
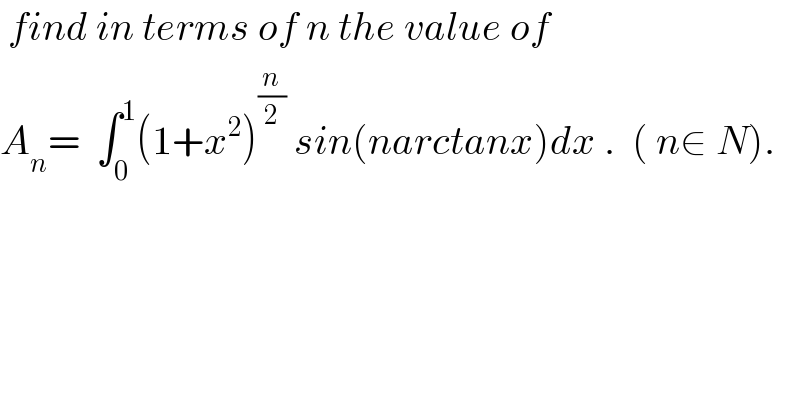 | ||
Commented by abdo imad last updated on 23/Jan/18 | ||
![let introduce the polynome P(x)= (1/(2i)) ((1+ix)^n −(1−ix)^n ) let write P(x) in geometric form .we have ∣1+ix∣= (√(1+x^2 ))= (1+x^2 )^(1/2) and 1+ix = (√(1+x^2 )) ( (1/(√(1+x^2 ))) +i(x/(√(1+x^2 ))))= r e^(iθ) ⇒ r=(√(1+x^2 )) and tanθ=x⇒ θ=artanx so (1+ix)^n = (1+x^2 )^(n/2) e^(inarctanx) (1−ix)^n =(1+x^2 )^(n/2) e^(−inartanx) and P(x)=(1/(2i))( 2iIm((1+ix)^n ))= (1+x^2 )^(n/2) sin(narctanx) ⇒ A_n =∫_0 ^1 P(x)dx but we have proved that P(x)= Σ_(p=0) ^([((n−1)/2)]) (−1)^p C_n ^(2p+1) x^(2p+1) ∫_0 ^1 P(x)dx = Σ_(p=0) ^([((n−1)/2)]) (−1)^p (C_n ^(2p+1) /(2p+2)) = A_n .](Q28282.png) | ||