Question Number 28411 by ajfour last updated on 25/Jan/18
Commented by ajfour last updated on 25/Jan/18
$${The}\:{smaller}\:{sphere}\:{touches}\:{the} \\ $$$${paraboloid}\:{only}\:{at}\:{inner}\:{bottommost}, \\ $$$${point}.\:{Find}\:{the}\:{smallest}\:{value} \\ $$$${of}\:\boldsymbol{{R}}\:{in}\:{terms}\:{of}\:\boldsymbol{{r}},\:{if}\:{the}\:{larger} \\ $$$${sphere}\:{touches}\:{the}\:{smaller}\:{sphere} \\ $$$${and}\:{also}\:{the}\:{walls}\:{of}\:{the}\: \\ $$$${paraboloid}. \\ $$
Answered by ajfour last updated on 25/Jan/18
$${let}\:{eq}.\:{of}\:{parabola}\:{in}\:{the}\:{plane}\:{be} \\ $$$${be}\:\:\:\boldsymbol{{y}}=\boldsymbol{{Ax}}^{\mathrm{2}} . \\ $$$${eq}\:{of}\:{circle}\:{with}\:{radius}\:{r}: \\ $$$${x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\: \\ $$$${since}\:{smaller}\:{circle}\:{touches} \\ $$$${parabola}\:{at}\:{vertex}\:{only}\:{the}\:{origin} \\ $$$${is}\:{to}\:{satisfy}\:{simultaneously}\:{the} \\ $$$${eq}.\:{of}\:{smaller}\:{circle}\:{and}\:{sphere} \\ $$$${and}\:{for}\:{R}\:{to}\:{be}\:{least}\:{we}\:{are}\:{to} \\ $$$${have}\:{all}\:{four}\:{roots}\:{real}\:\:{namely} \\ $$$${x}=\mathrm{0}.\:{Hrnce} \\ $$$${x}^{\mathrm{2}} +\left({Ax}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{A}^{\mathrm{2}} {x}^{\mathrm{4}} +\left(\mathrm{1}−\mathrm{2}{Ar}\right){x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} \left({A}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{Ar}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{A}=\frac{\mathrm{1}}{\mathrm{2}{r}} \\ $$$${Eq}.\:{of}\:{bigger}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{2}{r}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${eq}.\:{of}\:{tangent}\:{to}\:{this}\:{circle} \\ $$$${x}_{\mathrm{1}} \left({x}−{x}_{\mathrm{1}} \right)+\left({y}_{\mathrm{1}} −\mathrm{2}{r}−{R}\right)\left({y}−{y}_{\mathrm{1}} \right)=\mathrm{0} \\ $$$${tangent}\:{to}\:{parabola} \\ $$$$\frac{{y}+{y}_{\mathrm{1}} }{\mathrm{2}}=\frac{{xx}_{\mathrm{1}} }{\mathrm{2}{r}}\:\Rightarrow\:{xx}_{\mathrm{1}} −{r}\left({y}+{y}_{\mathrm{1}} \right)=\mathrm{0} \\ $$$${for}\:{both}\:{tangents}\:{to}\:{be}\:{same}\:{then} \\ $$$${comparing}\:{coefficient}\:{of}\:{y}\:: \\ $$$$\:\mathrm{2}{r}+{R}−{y}_{\mathrm{1}} ={r}\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow\:{y}_{\mathrm{1}} ={r}+{R} \\ $$$$\:{As}\:\left({x}_{\mathrm{1}} ,\:{y}_{\mathrm{1}} \right)\:{is}\:{on}\:{parabola},\:{so} \\ $$$${y}_{\mathrm{1}} =\frac{{x}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}{r}}\:\:\:\:\Rightarrow\:\:{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2}{r}\left({r}+{R}\right) \\ $$$${since}\:\:{x}_{\mathrm{1}} ^{\mathrm{2}} +\left({y}_{\mathrm{1}} −\mathrm{2}{r}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\mathrm{2}{r}\left({R}+{r}\right)+{r}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{R}^{\:\mathrm{2}} −\mathrm{2}{rR}−\mathrm{3}{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\left({R}−{r}\right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:{or}\:\:\:{R}=\mathrm{3}{r}\:\:. \\ $$
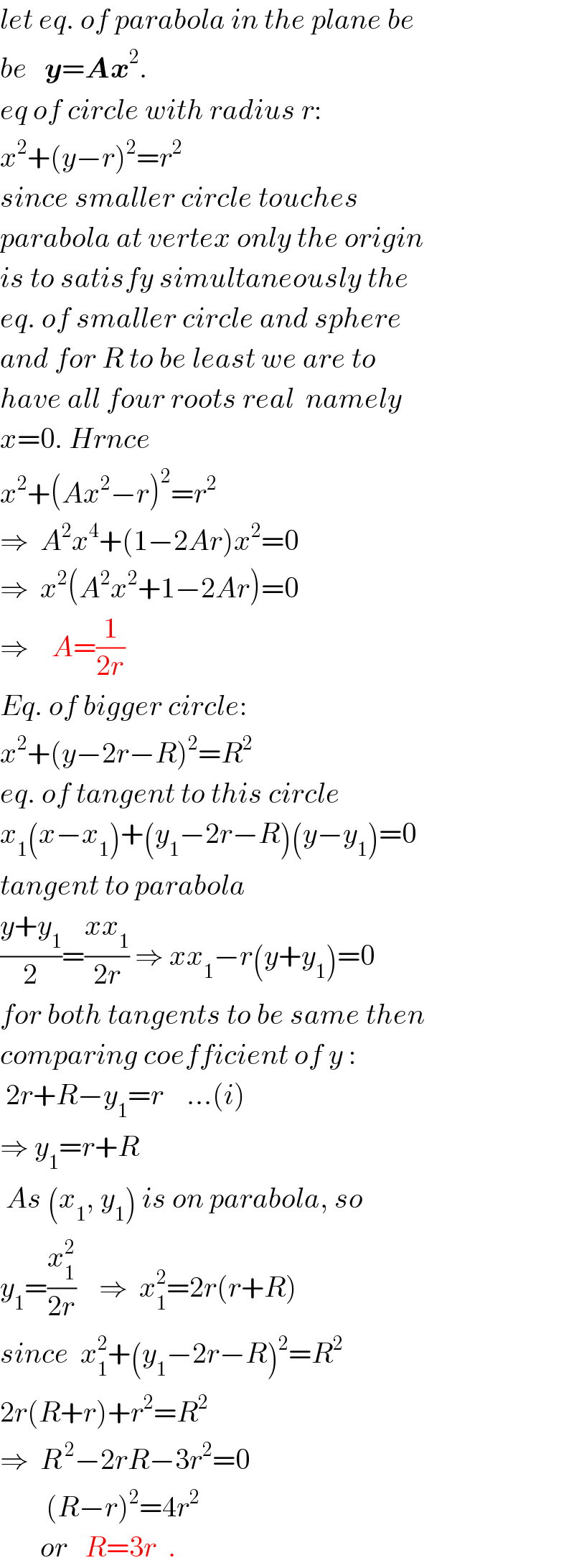
Commented by mrW2 last updated on 25/Jan/18
$${I}\:{think}\:{there}\:{is}\:{following}\:{relation}: \\ $$$${the}\:{first}\:{circle}\:{r}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{A}}={r} \\ $$$${the}\:{second}\:{circle}\:{r}_{\mathrm{2}} \left(={R}\right)=\frac{\mathrm{3}}{\mathrm{2}{A}}=\mathrm{3}{r} \\ $$$${the}\:{third}\:{circle}\:{r}_{\mathrm{3}} =\frac{\mathrm{5}}{\mathrm{2}{A}}=\mathrm{5}{r} \\ $$$$.... \\ $$$${the}\:{n}−{th}\:{circle}\:{r}_{{n}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{A}}=\left(\mathrm{2}{n}−\mathrm{1}\right){r} \\ $$
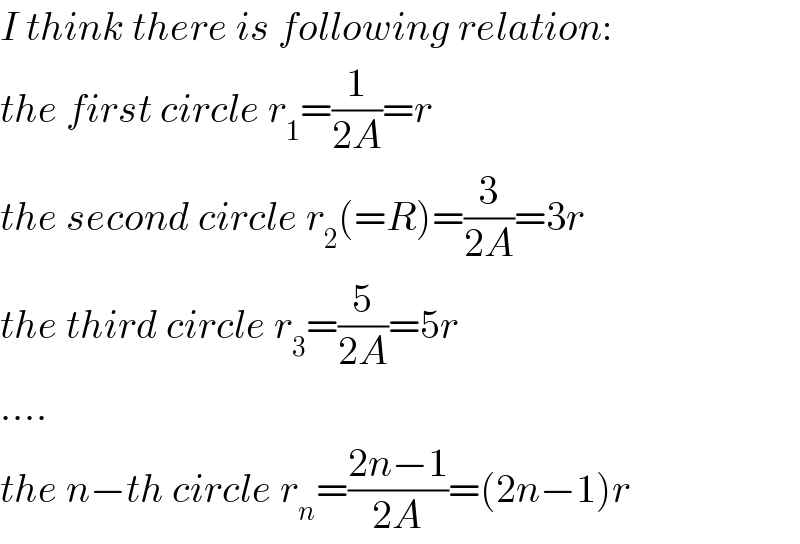
Commented by ajfour last updated on 26/Jan/18
$${i}\:{had}\:{suspected}\:{so}.\:{Thanks}\:{Sir}. \\ $$
Answered by mrW2 last updated on 25/Jan/18
![let the eqn. of parabola be y=ax^2 eqn. of circle r: x^2 +(y−r)^2 =r^2 x^2 +(ax^2 −r)^2 =r^2 a^2 x^4 −(2ar−1)x^2 =0 x^2 [a^2 x^2 −(2ar−1)]=0 x=0 x^2 =((2ar−1)/a^2 ) so that the circle touches the parabola only at one point x=0, ⇒2ar−1≤0 ⇒2ar≤1 eqn. of circle R: x^2 +(y−2r−R)^2 =R^2 x^2 +(ax^2 −2r−R)^2 =R^2 a^2 x^4 −[2a(2r+R)−1]x^2 +4r(r+R)=0 Δ=[2a(2r+R)−1]^2 −16a^2 r(r+R)=0 4a^2 (2r+R)^2 −4a(2r+R)+1−16a^2 r^2 −16a^2 rR=0 16a^2 r^2 +4a^2 R^2 +16a^2 rR−8ar−4aR+1−16a^2 r^2 −16a^2 rR=0 4(aR)^2 −4(aR)−(8ar−1)=0 aR=((4+(√(4^2 +4×4(8ar−1))))/(2×4))=((1+(√(8ar)))/2) R=((1+(√(8ar)))/(2ar))×r=((1+(√4))/1)r=3r](Q28418.png)
$${let}\:{the}\:{eqn}.\:{of}\:{parabola}\:{be} \\ $$$${y}={ax}^{\mathrm{2}} \\ $$$$ \\ $$$${eqn}.\:{of}\:{circle}\:{r}: \\ $$$${x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +\left({ax}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} {x}^{\mathrm{4}} −\left(\mathrm{2}{ar}−\mathrm{1}\right){x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left[{a}^{\mathrm{2}} {x}^{\mathrm{2}} −\left(\mathrm{2}{ar}−\mathrm{1}\right)\right]=\mathrm{0} \\ $$$${x}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{2}{ar}−\mathrm{1}}{{a}^{\mathrm{2}} } \\ $$$${so}\:{that}\:{the}\:{circle}\:{touches}\:{the}\:{parabola} \\ $$$${only}\:{at}\:{one}\:{point}\:{x}=\mathrm{0}, \\ $$$$\Rightarrow\mathrm{2}{ar}−\mathrm{1}\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{ar}\leqslant\mathrm{1} \\ $$$$ \\ $$$${eqn}.\:{of}\:{circle}\:{R}: \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{2}{r}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +\left({ax}^{\mathrm{2}} −\mathrm{2}{r}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} {x}^{\mathrm{4}} −\left[\mathrm{2}{a}\left(\mathrm{2}{r}+{R}\right)−\mathrm{1}\right]{x}^{\mathrm{2}} +\mathrm{4}{r}\left({r}+{R}\right)=\mathrm{0} \\ $$$$\Delta=\left[\mathrm{2}{a}\left(\mathrm{2}{r}+{R}\right)−\mathrm{1}\right]^{\mathrm{2}} −\mathrm{16}{a}^{\mathrm{2}} {r}\left({r}+{R}\right)=\mathrm{0} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{2}{r}+{R}\right)^{\mathrm{2}} −\mathrm{4}{a}\left(\mathrm{2}{r}+{R}\right)+\mathrm{1}−\mathrm{16}{a}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{16}{a}^{\mathrm{2}} {rR}=\mathrm{0} \\ $$$$\mathrm{16}{a}^{\mathrm{2}} {r}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {R}^{\mathrm{2}} +\mathrm{16}{a}^{\mathrm{2}} {rR}−\mathrm{8}{ar}−\mathrm{4}{aR}+\mathrm{1}−\mathrm{16}{a}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{16}{a}^{\mathrm{2}} {rR}=\mathrm{0} \\ $$$$\mathrm{4}\left({aR}\right)^{\mathrm{2}} −\mathrm{4}\left({aR}\right)−\left(\mathrm{8}{ar}−\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$${aR}=\frac{\mathrm{4}+\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{4}×\mathrm{4}\left(\mathrm{8}{ar}−\mathrm{1}\right)}}{\mathrm{2}×\mathrm{4}}=\frac{\mathrm{1}+\sqrt{\mathrm{8}{ar}}}{\mathrm{2}} \\ $$$${R}=\frac{\mathrm{1}+\sqrt{\mathrm{8}{ar}}}{\mathrm{2}{ar}}×{r}=\frac{\mathrm{1}+\sqrt{\mathrm{4}}}{\mathrm{1}}{r}=\mathrm{3}{r} \\ $$
Commented by ajfour last updated on 25/Jan/18
$${Thanks}\:{for}\:{confirming},\:{Sir}! \\ $$