
Question and Answers Forum
Question Number 28427 by abdo imad last updated on 25/Jan/18
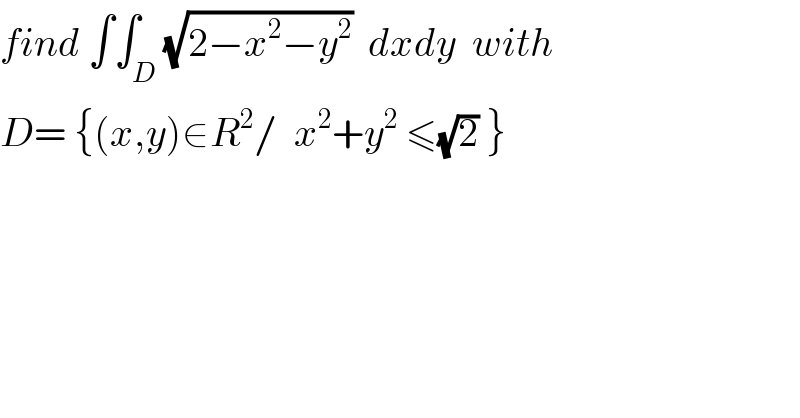
Commented by abdo imad last updated on 27/Jan/18
![let put I= ∫∫_D (√(2−x^2 −y^2 )) let use the ch. x=rcosθ and y=rsinθ x^2 +y^2 ≤(√2) ⇒ 0< r^2 ≤(√2)⇒ 0<r≤^4 (√2) I= ∫∫_(0<r≤^4 (√2) and 0≤θ≤2π) (√(2−r^2 )) rdrdθ I= (∫_0 ^4_(√2) r(√(2−r^2 )) dr) ( ∫_0 ^(2π) θ) =2π ∫_0 ^4_(√2) r(√(2−r^2 )) dr =−((2π)/3)∫_0 ^4_(√2) 3 (−r)(2−r^2 )^(1/2) dr =−((2π)/3) [ (2−r^2 )^(3/2) ]_0 ^4_(√2) = ((−2π)/3)((2 −(^4 (√(2))) )^2 )^(3/2) −2^(3/2) ) =((−2π)/3) ( (2−(√(2)))^(3/2) −2(√2)) = ((−2π)/3)( (2−(√(2))) (√(2−(√2))) −2(√2))) .](Q28570.png)
Answered by ajfour last updated on 27/Jan/18
![I=∫_0 ^( 2π) [(1/2)∫_0 ^( (√2)) (√(2−(r^2 ))) d(r^2 )]dθ =[((2π(2−r^2 )(√(2−r^2 )))/3)]∣_(r^2 =(√2)) ^0 I = ((2π)/3)[2(√2)−(2−(√2))(√(2−(√2))) ] .](Q28571.png)
| ||
Question and Answers Forum | ||
Question Number 28427 by abdo imad last updated on 25/Jan/18 | ||
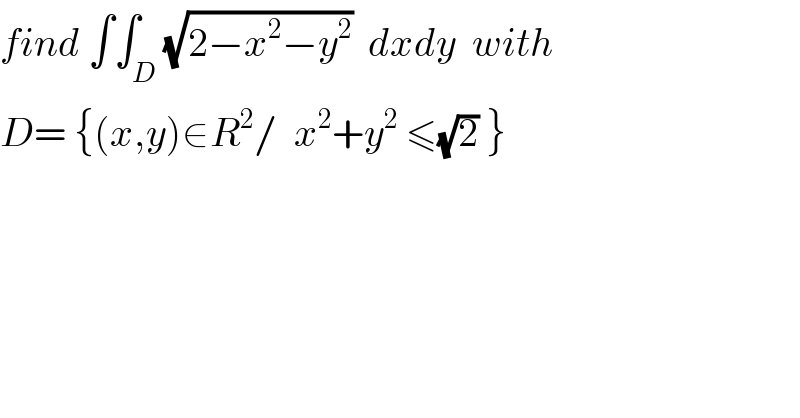 | ||
Commented by abdo imad last updated on 27/Jan/18 | ||
![let put I= ∫∫_D (√(2−x^2 −y^2 )) let use the ch. x=rcosθ and y=rsinθ x^2 +y^2 ≤(√2) ⇒ 0< r^2 ≤(√2)⇒ 0<r≤^4 (√2) I= ∫∫_(0<r≤^4 (√2) and 0≤θ≤2π) (√(2−r^2 )) rdrdθ I= (∫_0 ^4_(√2) r(√(2−r^2 )) dr) ( ∫_0 ^(2π) θ) =2π ∫_0 ^4_(√2) r(√(2−r^2 )) dr =−((2π)/3)∫_0 ^4_(√2) 3 (−r)(2−r^2 )^(1/2) dr =−((2π)/3) [ (2−r^2 )^(3/2) ]_0 ^4_(√2) = ((−2π)/3)((2 −(^4 (√(2))) )^2 )^(3/2) −2^(3/2) ) =((−2π)/3) ( (2−(√(2)))^(3/2) −2(√2)) = ((−2π)/3)( (2−(√(2))) (√(2−(√2))) −2(√2))) .](Q28570.png) | ||
Answered by ajfour last updated on 27/Jan/18 | ||
![I=∫_0 ^( 2π) [(1/2)∫_0 ^( (√2)) (√(2−(r^2 ))) d(r^2 )]dθ =[((2π(2−r^2 )(√(2−r^2 )))/3)]∣_(r^2 =(√2)) ^0 I = ((2π)/3)[2(√2)−(2−(√2))(√(2−(√2))) ] .](Q28571.png) | ||
| ||