
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 28428 by abdo imad last updated on 25/Jan/18
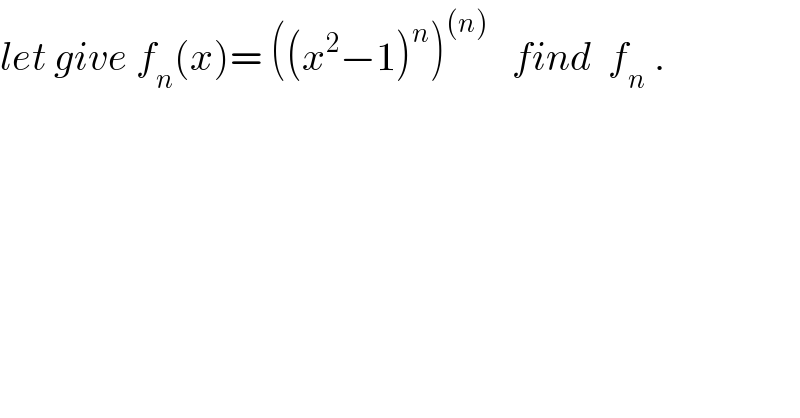
Commented by abdo imad last updated on 27/Jan/18
![we have f_n (x)= (p(x))^((n)) with p(x)=(x^2 −1)^n p(x)= Σ_(k=0) ^n C_n ^k x^(2k) (−1)^(n−k) =(−1)^n Σ_(k=0) ^n (−1)^k C_n ^k x^(2k) (p(x))^((n)) =(−1)^n Σ_(k=0) ^n (−1)^k C_n ^k (x^(2k) )^((n)) but if 2k<n (x^(2k) )^((n)) =0 so f_n (x)= (−1)^n Σ_(k=[((n−1)/2)] +1) ^n C_n ^k (x^(2k) )^((n)) .let find (x^p )^((n)) for p≥n wehave (x^p )^((1)) =p x^(p−1) ,(x^p )^((2)) =p(p−1)x^(p−2) so (x^p )^((n)) = p(p−1)....(p−n+1)x^(p−n) =((p(p−1)....(p−n+1)(p−n)!)/((p−n)!)) x^(p−n) =((p!)/((p−n)!)) x^(p−n) ⇒ (x^(2k) )^((n)) = (((2k)!)/((2k−n)!)) x^(2k−n) so f_n (x)= (−1)^n Σ_(k=[((n−1)/2)]+1) ^n C_n ^k (((2k)!)/((2k−n)!)) x^(2k−n) .](Q28572.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 28428 by abdo imad last updated on 25/Jan/18 | ||
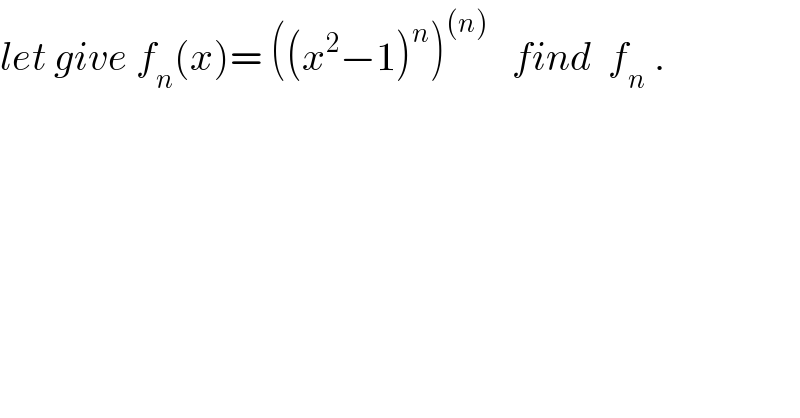 | ||
Commented by abdo imad last updated on 27/Jan/18 | ||
![we have f_n (x)= (p(x))^((n)) with p(x)=(x^2 −1)^n p(x)= Σ_(k=0) ^n C_n ^k x^(2k) (−1)^(n−k) =(−1)^n Σ_(k=0) ^n (−1)^k C_n ^k x^(2k) (p(x))^((n)) =(−1)^n Σ_(k=0) ^n (−1)^k C_n ^k (x^(2k) )^((n)) but if 2k<n (x^(2k) )^((n)) =0 so f_n (x)= (−1)^n Σ_(k=[((n−1)/2)] +1) ^n C_n ^k (x^(2k) )^((n)) .let find (x^p )^((n)) for p≥n wehave (x^p )^((1)) =p x^(p−1) ,(x^p )^((2)) =p(p−1)x^(p−2) so (x^p )^((n)) = p(p−1)....(p−n+1)x^(p−n) =((p(p−1)....(p−n+1)(p−n)!)/((p−n)!)) x^(p−n) =((p!)/((p−n)!)) x^(p−n) ⇒ (x^(2k) )^((n)) = (((2k)!)/((2k−n)!)) x^(2k−n) so f_n (x)= (−1)^n Σ_(k=[((n−1)/2)]+1) ^n C_n ^k (((2k)!)/((2k−n)!)) x^(2k−n) .](Q28572.png) | ||