
Question and Answers Forum
Question Number 28429 by abdo imad last updated on 25/Jan/18
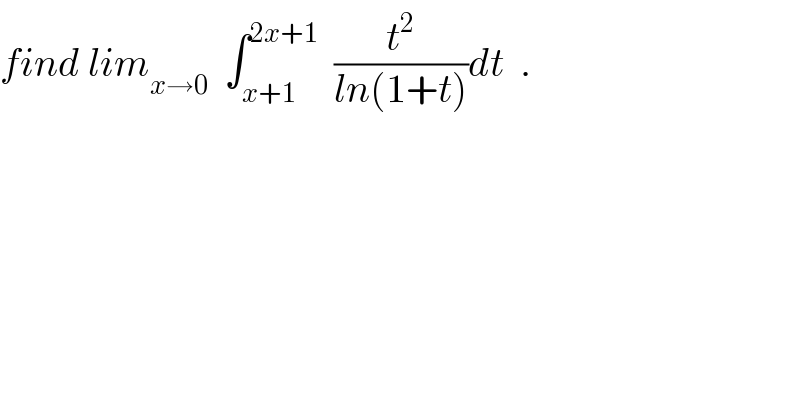
Commented by abdo imad last updated on 27/Jan/18
![∃ c ∈]x+1,2x+1[/ ∫_(x+1) ^(2x+1) = (1/(ln(1+c))) ∫_(x+1) ^(2x+1) t^2 dt = (1/3) (1/(ln(1+c))) ( (2x+1)^3 − (x+1)^3 ) we have x→0 ⇒ c→1 and lim_(x→0 ) ∫_(x+1) ^(2x+1) (t^2 /(ln(1+t)))dt =(1/(3ln2))×0=0 (look that the function w(t)= (1/(ln(1+t))) is continue on [x+1,2x+1] .)](Q28576.png)
| ||
Question and Answers Forum | ||
Question Number 28429 by abdo imad last updated on 25/Jan/18 | ||
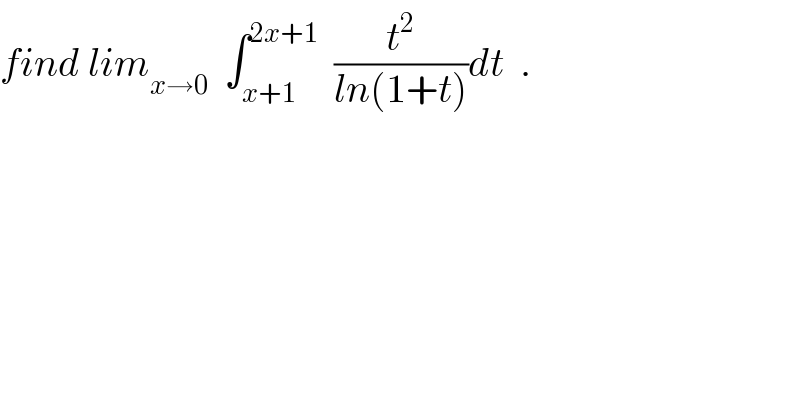 | ||
Commented by abdo imad last updated on 27/Jan/18 | ||
![∃ c ∈]x+1,2x+1[/ ∫_(x+1) ^(2x+1) = (1/(ln(1+c))) ∫_(x+1) ^(2x+1) t^2 dt = (1/3) (1/(ln(1+c))) ( (2x+1)^3 − (x+1)^3 ) we have x→0 ⇒ c→1 and lim_(x→0 ) ∫_(x+1) ^(2x+1) (t^2 /(ln(1+t)))dt =(1/(3ln2))×0=0 (look that the function w(t)= (1/(ln(1+t))) is continue on [x+1,2x+1] .)](Q28576.png) | ||