
Question and Answers Forum
Question Number 28432 by abdo imad last updated on 25/Jan/18
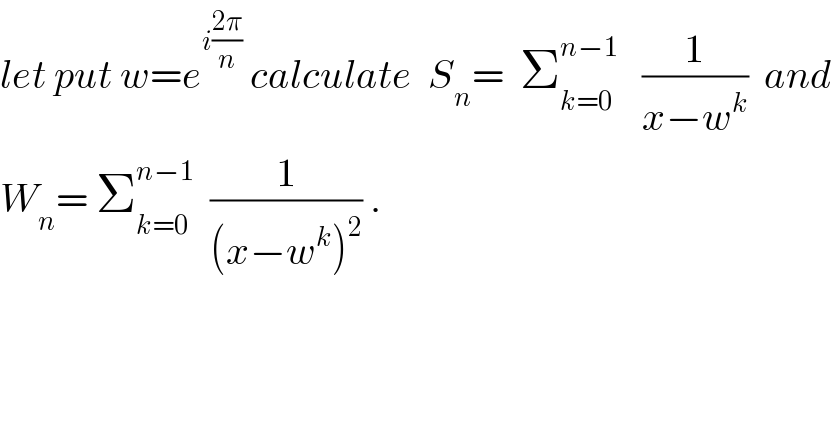
Commented by abdo imad last updated on 27/Jan/18
![let introduce the polynomial p(x)= x^n −1 the roots of p(x)are the complex z_k =e^(i((2kπ)/n)) and k∈[[0,n−1]] we know that ((p^′ (x))/(p(x))) = Σ_(k=0) ^(n−1) (1/(x−z_k )) =Σ_(k=0) ^(n−1) (1/(x−w^k )) so S_n = ((nx^(n−1) )/(x^n −1)) also we have by derivation (d/dx)( ((p^′ (x))/(p(x))))=−Σ_(k=0) ^(n−1) (1/((x−w^k )^2 )) ⇒((p^(′′) (x)p(x) −(p^′ (x))^2 )/((p(x))^2 ))=−Σ_(k=0) ^(n−1) (1/((x−w^k )^2 )) W_n =−((n(n−1)x^(n−2) ( x^n −1) −(nx^(n−1) )^2 )/((x^n −1)^2 )) =−((n(n−1) x^(2n−2) −n(n−1)x^(n−2) −n^2 x^(2n−2) )/((x^n −1)^2 )) =−((−n x^(2n−2) −n(n−1)x^(n−2) )/((x^n −1)^2 ))=((n x^(2n−2) −n(n−1)x^(n−2) )/((x^n −1)^2 )) for n≥2 .](Q28579.png)
| ||
Question and Answers Forum | ||
Question Number 28432 by abdo imad last updated on 25/Jan/18 | ||
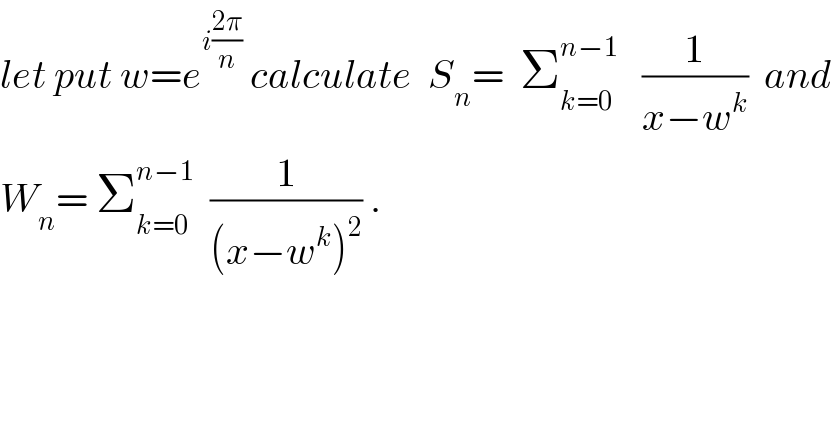 | ||
Commented by abdo imad last updated on 27/Jan/18 | ||
![let introduce the polynomial p(x)= x^n −1 the roots of p(x)are the complex z_k =e^(i((2kπ)/n)) and k∈[[0,n−1]] we know that ((p^′ (x))/(p(x))) = Σ_(k=0) ^(n−1) (1/(x−z_k )) =Σ_(k=0) ^(n−1) (1/(x−w^k )) so S_n = ((nx^(n−1) )/(x^n −1)) also we have by derivation (d/dx)( ((p^′ (x))/(p(x))))=−Σ_(k=0) ^(n−1) (1/((x−w^k )^2 )) ⇒((p^(′′) (x)p(x) −(p^′ (x))^2 )/((p(x))^2 ))=−Σ_(k=0) ^(n−1) (1/((x−w^k )^2 )) W_n =−((n(n−1)x^(n−2) ( x^n −1) −(nx^(n−1) )^2 )/((x^n −1)^2 )) =−((n(n−1) x^(2n−2) −n(n−1)x^(n−2) −n^2 x^(2n−2) )/((x^n −1)^2 )) =−((−n x^(2n−2) −n(n−1)x^(n−2) )/((x^n −1)^2 ))=((n x^(2n−2) −n(n−1)x^(n−2) )/((x^n −1)^2 )) for n≥2 .](Q28579.png) | ||