
Question and Answers Forum
Question Number 28533 by abdo imad last updated on 26/Jan/18
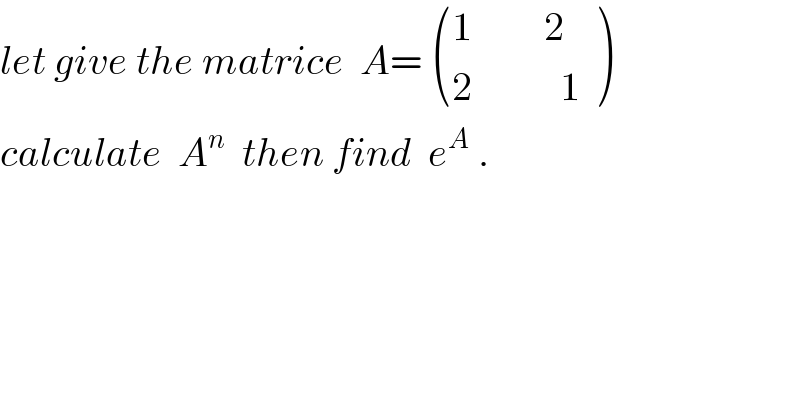
Commented by abdo imad last updated on 28/Jan/18
![we have A = I +2J with I = (((1 0)),((0 1)) ) and J= (((0 1)),((1 0 )) ) we have J^2 = I ⇒ J^(2n) =I and J^(2n+1) =J A= I +2J with the condition IJ=JI A^n =(2J +I)^n = Σ_(k=0) ^n C_n ^k (2J)^k = Σ_(k=0) ^n 2^k C_n ^k J^k = Σ(_(k=2p) ...) +Σ_(k=2p+1) (...) = Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p ) I +Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) J = (((Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) 0 )),((0 Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) )) ) + (((0 Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) )),((Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) 0)) ) = (((x_n y_n )),(y_(n x_n ) ) ) with x_n = Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) and y_n =Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) . e^A = Σ_(n=0) ^∞ (A^n /(n!))= ((( Σ (x_n /(n!)) Σ(y_n /(n!)) )),((Σ(y_n /(n!)) Σ(x_n /(n!)) )) )](Q28669.png)
| ||
Question and Answers Forum | ||
Question Number 28533 by abdo imad last updated on 26/Jan/18 | ||
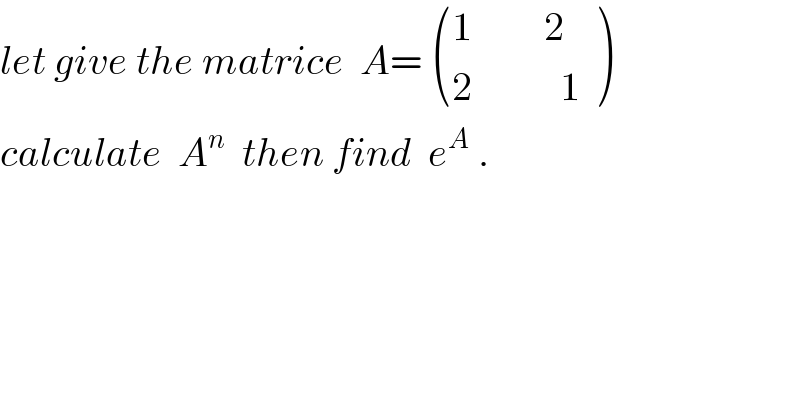 | ||
Commented by abdo imad last updated on 28/Jan/18 | ||
![we have A = I +2J with I = (((1 0)),((0 1)) ) and J= (((0 1)),((1 0 )) ) we have J^2 = I ⇒ J^(2n) =I and J^(2n+1) =J A= I +2J with the condition IJ=JI A^n =(2J +I)^n = Σ_(k=0) ^n C_n ^k (2J)^k = Σ_(k=0) ^n 2^k C_n ^k J^k = Σ(_(k=2p) ...) +Σ_(k=2p+1) (...) = Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p ) I +Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) J = (((Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) 0 )),((0 Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) )) ) + (((0 Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) )),((Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) 0)) ) = (((x_n y_n )),(y_(n x_n ) ) ) with x_n = Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) and y_n =Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) . e^A = Σ_(n=0) ^∞ (A^n /(n!))= ((( Σ (x_n /(n!)) Σ(y_n /(n!)) )),((Σ(y_n /(n!)) Σ(x_n /(n!)) )) )](Q28669.png) | ||