Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2857 by Syaka last updated on 29/Nov/15

By Induction Prove that : 12∣(n^4 − n^2 )

$${By}\:{Induction}\:{Prove}\:{that}\:: \\ $$$$ \\ $$$$\mathrm{12}\mid\left({n}^{\mathrm{4}} \:−\:{n}^{\mathrm{2}} \right) \\ $$

Commented by Filup last updated on 29/Nov/15

What does ∣ mean?

$$\mathrm{What}\:\mathrm{does}\:\mid\:\mathrm{mean}? \\ $$

Commented by prakash jain last updated on 29/Nov/15

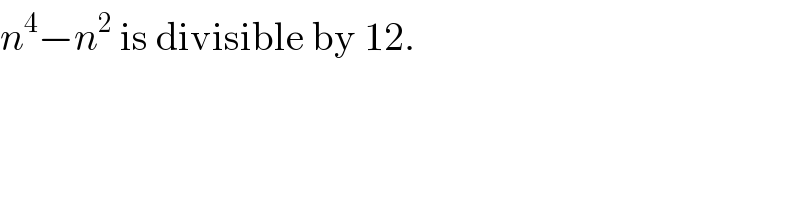
n^4 −n^2 is divisible by 12.

$${n}^{\mathrm{4}} −{n}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{12}. \\ $$

Commented by Syaka last updated on 29/Nov/15

yes, Sir

$${yes},\:{Sir} \\ $$

Answered by prakash jain last updated on 29/Nov/15

f(n)=n^2 (n+1)(n−1)=(n−1)n(n+1)n Statement 1. g(n)=(n−1)n is divisible by 2. ...(A) g(1)=0, g(2)=2 Let us say 2∣g(n) for some n so n(n−1)=2k g(n+1)=(n+1)n=n^2 +n=n^2 −n+2n=2(k+n) So the statement (A) is true ∀n. It follows that h(n)=n(n+1) is divisible by 2. f(n)=g(n)h(n) is divisible by 4. ...(B) Statement 2: y(n)=(n−1)n(n+1) is divisible by 3. ...(C) y(1)=0 Let us y(n) is divisible by 3 for some n. y(n)=(n−1)n(n+1)=3j y(n+1)=n(n+1)(n+2)=n(n+1)(n−1+3) =n(n+1)(n−1)+3n(n+1)=3j+3n(n+1) =3(j+n^2 +n) Hence y(n) is divisible by 3 for all n. From statement (B) and (C) f(n)=(n−1)n(n+1)n is divisible 4×3=12 since 3 and 4 don′t have a common factor.

$${f}\left({n}\right)={n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)=\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right){n} \\ $$$$\mathrm{Statement}\:\mathrm{1}. \\ $$$${g}\left({n}\right)=\left({n}−\mathrm{1}\right){n}\:\mathrm{is}\:\mathrm{divisible}\:{by}\:\mathrm{2}.\:\:\:...\left(\mathrm{A}\right) \\ $$$${g}\left(\mathrm{1}\right)=\mathrm{0}, \\ $$$${g}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:\mathrm{2}\mid{g}\left({n}\right)\:\mathrm{for}\:\mathrm{some}\:{n}\:\mathrm{so}\:{n}\left({n}−\mathrm{1}\right)=\mathrm{2}{k} \\ $$$${g}\left({n}+\mathrm{1}\right)=\left({n}+\mathrm{1}\right){n}={n}^{\mathrm{2}} +{n}={n}^{\mathrm{2}} −{n}+\mathrm{2}{n}=\mathrm{2}\left({k}+{n}\right) \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{statement}\:\left(\mathrm{A}\right)\:\mathrm{is}\:\mathrm{true}\:\forall{n}. \\ $$$$\mathrm{It}\:\mathrm{follows}\:\mathrm{that}\:{h}\left({n}\right)={n}\left({n}+\mathrm{1}\right)\: \\ $$$$\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2}.\:\:\:\: \\ $$$${f}\left({n}\right)={g}\left({n}\right){h}\left({n}\right)\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}.\:\:\:\:\:\:...\left({B}\right) \\ $$$$\mathrm{Statement}\:\mathrm{2}: \\ $$$${y}\left({n}\right)=\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)\:\mathrm{is}\:\mathrm{divisible}\:{by}\:\mathrm{3}.\:\:...\left(\mathrm{C}\right) \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{Let}\:\mathrm{us}\:{y}\left({n}\right)\:\mathrm{is}\:\mathrm{divisible}\:{by}\:\mathrm{3}\:\mathrm{for}\:\mathrm{some}\:{n}. \\ $$$${y}\left({n}\right)=\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)=\mathrm{3}{j} \\ $$$${y}\left({n}+\mathrm{1}\right)={n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)={n}\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={n}\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)+\mathrm{3}{n}\left({n}+\mathrm{1}\right)=\mathrm{3}{j}+\mathrm{3}{n}\left({n}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{j}+{n}^{\mathrm{2}} +{n}\right) \\ $$$${H}\mathrm{ence}\:{y}\left({n}\right)\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3}\:\mathrm{for}\:\mathrm{all}\:{n}. \\ $$$$\mathrm{From}\:\mathrm{statement}\:\left(\mathrm{B}\right)\:\mathrm{and}\:\left(\mathrm{C}\right) \\ $$$${f}\left({n}\right)=\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right){n}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{4}×\mathrm{3}=\mathrm{12} \\ $$$$\mathrm{since}\:\mathrm{3}\:\mathrm{and}\:\mathrm{4}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{a}\:\mathrm{common}\:\mathrm{factor}. \\ $$

Commented by RasheedAhmad last updated on 29/Nov/15

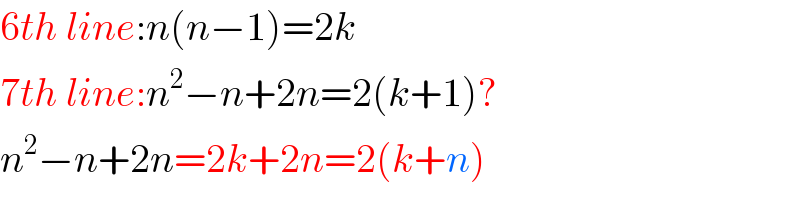
6th line:n(n−1)=2k 7th line:n^2 −n+2n=2(k+1)? n^2 −n+2n=2k+2n=2(k+n)

$$\mathrm{6}{th}\:{line}:{n}\left({n}−\mathrm{1}\right)=\mathrm{2}{k} \\ $$$$\mathrm{7}{th}\:{line}:{n}^{\mathrm{2}} −{n}+\mathrm{2}{n}=\mathrm{2}\left({k}+\mathrm{1}\right)? \\ $$$${n}^{\mathrm{2}} −{n}+\mathrm{2}{n}=\mathrm{2}{k}+\mathrm{2}{n}=\mathrm{2}\left({k}+{n}\right) \\ $$

Commented by prakash jain last updated on 29/Nov/15

Thanks Rasheed. I have corrected the mistake.

$$\mathrm{Thanks}\:\mathrm{Rasheed}. \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{corrected}\:\mathrm{the}\:\mathrm{mistake}. \\ $$

Commented by Rasheed Soomro last updated on 29/Nov/15

g(n+1)=(n+1)n=n^2 +n=n^2 −n+2n=2(k+n) So the statement (A) is true ∀n. How is 2(k+n) of the type (n−1)n g(n)=(n−1)n g(n+1)=2(k+n) On lhs n+1 indicates that you are seeking result for n+1,but on rhs you reached at 2(k+n) [instead of (n+1^(−) −1)(n+1)] Why So the statement (A) is true ∀n.?

$${g}\left({n}+\mathrm{1}\right)=\left({n}+\mathrm{1}\right){n}={n}^{\mathrm{2}} +{n}={n}^{\mathrm{2}} −{n}+\mathrm{2}{n}=\mathrm{2}\left({k}+{n}\right) \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{statement}\:\left(\mathrm{A}\right)\:\mathrm{is}\:\mathrm{true}\:\forall{n}. \\ $$$${How}\:{is}\:\mathrm{2}\left({k}+{n}\right)\:{of}\:{the}\:{type}\:\left({n}−\mathrm{1}\right){n} \\ $$$${g}\left({n}\right)=\left({n}−\mathrm{1}\right){n} \\ $$$${g}\left({n}+\mathrm{1}\right)=\mathrm{2}\left({k}+{n}\right) \\ $$$$\mathcal{O}{n}\:{lhs}\:{n}+\mathrm{1}\:{indicates}\:{that}\:{you}\:{are}\:{seeking}\: \\ $$$${result}\:{for}\:{n}+\mathrm{1},{but}\:{on}\:{rhs}\:{you}\:{reached}\:{at}\:\mathrm{2}\left({k}+{n}\right) \\ $$$$\left[{instead}\:{of}\:\left(\overline {{n}+\mathrm{1}}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)\right] \\ $$$${Why}\:\mathrm{So}\:\mathrm{the}\:\mathrm{statement}\:\left(\mathrm{A}\right)\:\mathrm{is}\:\mathrm{true}\:\forall{n}.? \\ $$

Commented by prakash jain last updated on 29/Nov/15

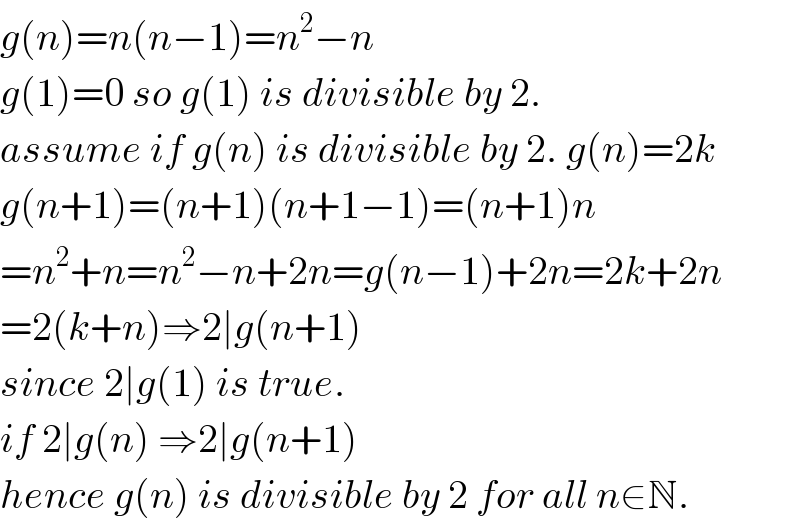
g(n)=n(n−1)=n^2 −n g(1)=0 so g(1) is divisible by 2. assume if g(n) is divisible by 2. g(n)=2k g(n+1)=(n+1)(n+1−1)=(n+1)n =n^2 +n=n^2 −n+2n=g(n−1)+2n=2k+2n =2(k+n)⇒2∣g(n+1) since 2∣g(1) is true. if 2∣g(n) ⇒2∣g(n+1) hence g(n) is divisible by 2 for all n∈N.

$${g}\left({n}\right)={n}\left({n}−\mathrm{1}\right)={n}^{\mathrm{2}} −{n}\: \\ $$$${g}\left(\mathrm{1}\right)=\mathrm{0}\:{so}\:{g}\left(\mathrm{1}\right)\:{is}\:{divisible}\:{by}\:\mathrm{2}. \\ $$$${assume}\:{if}\:{g}\left({n}\right)\:{is}\:{divisible}\:{by}\:\mathrm{2}.\:{g}\left({n}\right)=\mathrm{2}{k} \\ $$$${g}\left({n}+\mathrm{1}\right)=\left({n}+\mathrm{1}\right)\left({n}+\mathrm{1}−\mathrm{1}\right)=\left({n}+\mathrm{1}\right){n} \\ $$$$={n}^{\mathrm{2}} +{n}={n}^{\mathrm{2}} −{n}+\mathrm{2}{n}={g}\left({n}−\mathrm{1}\right)+\mathrm{2}{n}=\mathrm{2}{k}+\mathrm{2}{n} \\ $$$$=\mathrm{2}\left({k}+{n}\right)\Rightarrow\mathrm{2}\mid{g}\left({n}+\mathrm{1}\right) \\ $$$${since}\:\mathrm{2}\mid{g}\left(\mathrm{1}\right)\:{is}\:{true}. \\ $$$${if}\:\mathrm{2}\mid{g}\left({n}\right)\:\Rightarrow\mathrm{2}\mid{g}\left({n}+\mathrm{1}\right) \\ $$$${hence}\:{g}\left({n}\right)\:{is}\:{divisible}\:{by}\:\mathrm{2}\:{for}\:{all}\:{n}\in\mathbb{N}. \\ $$

Commented by Rasheed Soomro last updated on 30/Nov/15

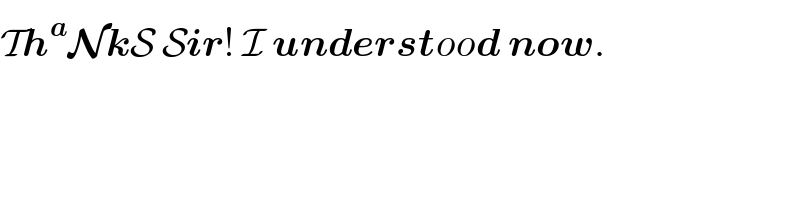
Th^a NkS Sir! I understood now.

$$\mathcal{T}\boldsymbol{{h}}^{\boldsymbol{{a}}} \boldsymbol{\mathcal{N}{k}}\mathcal{S}\:\mathcal{S}\boldsymbol{{ir}}!\:\mathcal{I}\:\boldsymbol{{underst}}{oo}\boldsymbol{{d}}\:\boldsymbol{{now}}. \\ $$

Commented by Rasheed Soomro last updated on 30/Nov/15

EXCELLENT Approach!

$$\boldsymbol{\mathcal{EXCELLENT}}\:\boldsymbol{\mathcal{A}{pproach}}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com