Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2859 by Syaka last updated on 29/Nov/15

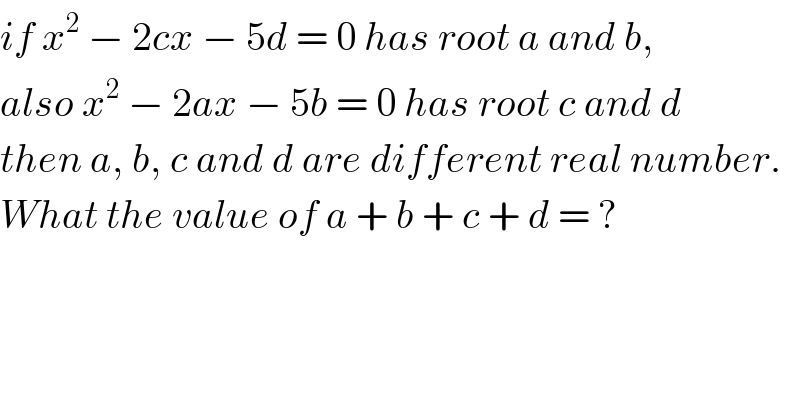
if x^2 − 2cx − 5d = 0 has root a and b, also x^2 − 2ax − 5b = 0 has root c and d then a, b, c and d are different real number. What the value of a + b + c + d = ?

$${if}\:{x}^{\mathrm{2}} \:−\:\mathrm{2}{cx}\:−\:\mathrm{5}{d}\:=\:\mathrm{0}\:{has}\:{root}\:{a}\:{and}\:{b}, \\ $$$${also}\:{x}^{\mathrm{2}} \:−\:\mathrm{2}{ax}\:−\:\mathrm{5}{b}\:=\:\mathrm{0}\:{has}\:{root}\:{c}\:{and}\:{d} \\ $$$${then}\:{a},\:{b},\:{c}\:{and}\:{d}\:{are}\:{different}\:{real}\:{number}. \\ $$$${What}\:{the}\:{value}\:{of}\:{a}\:+\:{b}\:+\:{c}\:+\:{d}\:=\:? \\ $$

Commented by Syaka last updated on 29/Nov/15

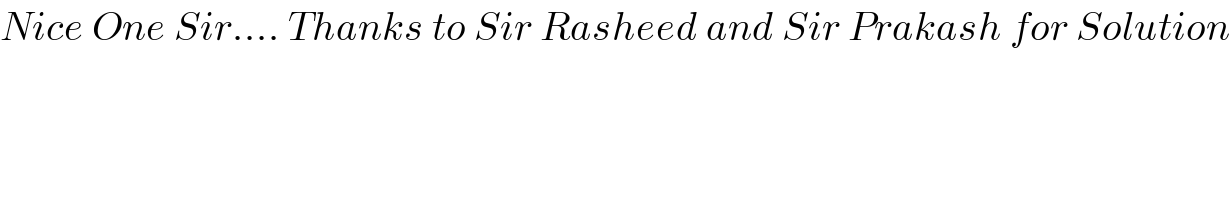
Nice One Sir.... Thanks to Sir Rasheed and Sir Prakash for Solution

$${Nice}\:{One}\:{Sir}....\:{Thanks}\:{to}\:{Sir}\:{Rasheed}\:{and}\:{Sir}\:{Prakash}\:{for}\:{Solution} \\ $$

Answered by Rasheed Soomro last updated on 29/Nov/15

x^2 − 2cx − 5d = 0 a,b are roots x^2 − 2ax − 5b = 0 c,d are roos a+b+c+d=? If ax^2 +bx+c=0 has α and β roots α+β=((−b)/a) and αβ=(c/a) Sum a+b=((−(−2c))/1)=2c..........(i) c+d=((−(−2a))/1)=2a..........(ii Adding (i) and (ii) a+b+c+d=2c+2a =2(a+c).....................(1) a+c=b+d Product ab=−5d and cd=−5b⇒abcd=25bd⇒ac=25⇒c=((25)/a).......(2) From (1) and ( 2) a+b+c+d=2(a+((25)/a)) a=((−(−2c)+(√((−2c)^2 −4(1)(−5d))))/(2(1)))=((2c+2(√(c^2 +5d)))/2) a =c+(√(c^2 +5d)) b =c−(√(c^2 +5d)) ⇒ a−b=2(√(c^2 +5d)) ⇒a^2 +b^2 −2ab=4c^2 +20d ⇒a^2 +b^2 −4c^2 =2ab+20d..........................(A) c=((−(−2a)+(√((−2a)^2 −4(1)(−5b))))/(2(1)))=((2a+2(√(a^2 +5b)))/2) c=a+(√(a^2 +5b)) d=a−(√(a^2 +5b)) ⇒ c−d=2(√(a^2 +5b)) ⇒c^2 +d^2 −2cd=4a^2 +20b ⇒−4a^2 +c^2 +d^2 =2cd+20b.........................(B) For complete solution (independant of a,b,c and d i−e constant) see the comment of Sir prakash jain below

$${x}^{\mathrm{2}} \:−\:\mathrm{2}{cx}\:−\:\mathrm{5}{d}\:=\:\mathrm{0}\:\:{a},{b}\:{are}\:{roots} \\ $$$$\:{x}^{\mathrm{2}} \:−\:\mathrm{2}{ax}\:−\:\mathrm{5}{b}\:=\:\mathrm{0}\:\:\:{c},{d}\:{are}\:{roos} \\ $$$${a}+{b}+{c}+{d}=? \\ $$$${If}\:\:\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0}\:{has}\:\:\alpha\:\:{and}\:\:\beta\:\:\:{roots} \\ $$$$\alpha+\beta=\frac{−{b}}{{a}}\:\:{and}\:\alpha\beta=\frac{{c}}{{a}} \\ $$$${Sum} \\ $$$${a}+{b}=\frac{−\left(−\mathrm{2}{c}\right)}{\mathrm{1}}=\mathrm{2}{c}..........\left({i}\right) \\ $$$${c}+{d}=\frac{−\left(−\mathrm{2}{a}\right)}{\mathrm{1}}=\mathrm{2}{a}..........\left({ii}\right. \\ $$$${Adding}\:\left({i}\right)\:{and}\:\left({ii}\right) \\ $$$${a}+{b}+{c}+{d}=\mathrm{2}{c}+\mathrm{2}{a}\:=\mathrm{2}\left({a}+{c}\right).....................\left(\mathrm{1}\right) \\ $$$${a}+{c}={b}+{d} \\ $$$${Product} \\ $$$${ab}=−\mathrm{5}{d}\:{and}\:{cd}=−\mathrm{5}{b}\Rightarrow{abcd}=\mathrm{25}{bd}\Rightarrow{ac}=\mathrm{25}\Rightarrow{c}=\frac{\mathrm{25}}{{a}}.......\left(\mathrm{2}\right) \\ $$$${From}\:\:\left(\mathrm{1}\right)\:\:{and}\:\:\left(\:\mathrm{2}\right) \\ $$$${a}+{b}+{c}+{d}=\mathrm{2}\left({a}+\frac{\mathrm{25}}{{a}}\right) \\ $$$${a}=\frac{−\left(−\mathrm{2}{c}\right)+\sqrt{\left(−\mathrm{2}{c}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{5}{d}\right)}}{\mathrm{2}\left(\mathrm{1}\right)}=\frac{\mathrm{2}{c}+\mathrm{2}\sqrt{{c}^{\mathrm{2}} +\mathrm{5}{d}}}{\mathrm{2}} \\ $$$$\:\:\:\:{a}\:={c}+\sqrt{{c}^{\mathrm{2}} +\mathrm{5}{d}} \\ $$$$\:\:\:\:{b}\:={c}−\sqrt{{c}^{\mathrm{2}} +\mathrm{5}{d}}\:\:\:\Rightarrow\:{a}−{b}=\mathrm{2}\sqrt{{c}^{\mathrm{2}} +\mathrm{5}{d}}\:\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}=\mathrm{4}{c}^{\mathrm{2}} +\mathrm{20}{d} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{4}{c}^{\mathrm{2}} =\mathrm{2}{ab}+\mathrm{20}{d}..........................\left({A}\right) \\ $$$${c}=\frac{−\left(−\mathrm{2}{a}\right)+\sqrt{\left(−\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{5}{b}\right)}}{\mathrm{2}\left(\mathrm{1}\right)}=\frac{\mathrm{2}{a}+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +\mathrm{5}{b}}}{\mathrm{2}} \\ $$$${c}={a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{5}{b}} \\ $$$${d}={a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{5}{b}}\:\:\Rightarrow\:{c}−{d}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +\mathrm{5}{b}}\:\Rightarrow{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}=\mathrm{4}{a}^{\mathrm{2}} +\mathrm{20}{b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{4}{a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{2}{cd}+\mathrm{20}{b}.........................\left({B}\right) \\ $$$$\mathcal{F}{or}\:{complete}\:{solution}\:\left({independant}\:{of}\:{a},{b},{c}\:{and}\:{d}\:\:{i}−{e}\:\:{constant}\right) \\ $$$${see}\:{the}\:{comment}\:{of}\:\mathcal{S}{ir}\:{prakash}\:{jain}\:{below} \\ $$$$ \\ $$

Commented by prakash jain last updated on 29/Nov/15

I think a+b+c+d should evaluate to a constant value since you have 4 variables and 4 equation that you derived.

$$\mathrm{I}\:\mathrm{think}\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\:\mathrm{should}\:\mathrm{evaluate}\:\mathrm{to}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{value}\:\mathrm{since}\:\mathrm{you}\:\mathrm{have}\:\mathrm{4}\:\mathrm{variables}\:\mathrm{and}\:\mathrm{4}\:\mathrm{equation} \\ $$$$\mathrm{that}\:\mathrm{you}\:\mathrm{derived}. \\ $$

Commented by Syaka last updated on 29/Nov/15

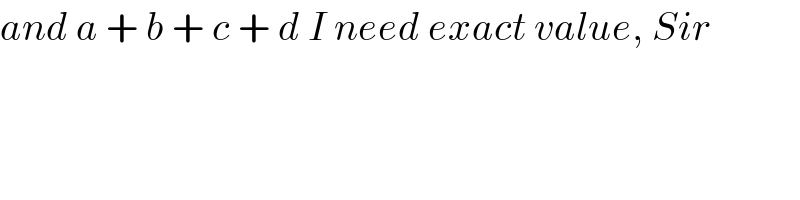
and a + b + c + d I need exact value, Sir

$${and}\:{a}\:+\:{b}\:+\:{c}\:+\:{d}\:{I}\:{need}\:{exact}\:{value},\:{Sir} \\ $$

Commented by RasheedAhmad last updated on 29/Nov/15

Nice Sir!

$$\mathcal{N}\boldsymbol{{ice}}\:\boldsymbol{\mathcal{S}{ir}}! \\ $$

Commented by prakash jain last updated on 29/Nov/15

Four equation given by Rasheed a+b=2c c+d=2a ab=−5d cd=−5b c=((25)/a) a+b=2c⇒b=((50−a^2 )/a) d=((−5b)/c)=((−5(50−a^2 ))/(a((25)/a)))=−((50−a^2 )/5) c+d=2a a=b=c=d=0 is trival solution ...(A) ((25)/a)−((50−a^2 )/5)=2a 125−50a+a^3 =10a^2 a^3 −10a^2 −50a+125=0 a^3 +5a^2 −15a^2 −75a+25a+125=0 (a+5)(a^2 −15a+25)=0 a=−5 or a=((15±(√(225−100)))/2)=((15±(√5))/2) a=−5, c=−5, b=−5, c=−5 ....(B) a=((15−(√5))/2),c=((25)/a)=((50)/(15−(√5)))=((50(15+(√5)))/(100))=((15+(√5))/2) b=2c−a=((15+15(√5))/2),d=((15−15(√5))/2) ...(C) similar you can get the last solution for a=((15+(√5))/2) a=((15+(√5))/2),c=((15−(√5))/2),b=((15−15(√5))/2), d=((15+15(√5))/2) ..(D) C ans D are only valid solutions for a,b,c,d are different. in both cases a+b+c+d=30

$$\mathrm{Four}\:\mathrm{equation}\:\mathrm{given}\:\mathrm{by}\:\mathrm{Rasheed} \\ $$$${a}+{b}=\mathrm{2}{c} \\ $$$${c}+{d}=\mathrm{2}{a} \\ $$$${ab}=−\mathrm{5}{d} \\ $$$${cd}=−\mathrm{5}{b} \\ $$$${c}=\frac{\mathrm{25}}{{a}} \\ $$$${a}+{b}=\mathrm{2}{c}\Rightarrow{b}=\frac{\mathrm{50}−{a}^{\mathrm{2}} }{{a}} \\ $$$${d}=\frac{−\mathrm{5}{b}}{{c}}=\frac{−\mathrm{5}\left(\mathrm{50}−{a}^{\mathrm{2}} \right)}{{a}\frac{\mathrm{25}}{{a}}}=−\frac{\mathrm{50}−{a}^{\mathrm{2}} }{\mathrm{5}} \\ $$$${c}+{d}=\mathrm{2}{a} \\ $$$${a}={b}={c}={d}=\mathrm{0}\:\mathrm{is}\:\mathrm{trival}\:\mathrm{solution}\:\:...\left({A}\right) \\ $$$$\frac{\mathrm{25}}{{a}}−\frac{\mathrm{50}−{a}^{\mathrm{2}} }{\mathrm{5}}=\mathrm{2}{a} \\ $$$$\mathrm{125}−\mathrm{50}{a}+{a}^{\mathrm{3}} =\mathrm{10}{a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} −\mathrm{10}{a}^{\mathrm{2}} −\mathrm{50}{a}+\mathrm{125}=\mathrm{0} \\ $$$${a}^{\mathrm{3}} +\mathrm{5}{a}^{\mathrm{2}} −\mathrm{15}{a}^{\mathrm{2}} −\mathrm{75}{a}+\mathrm{25}{a}+\mathrm{125}=\mathrm{0} \\ $$$$\left({a}+\mathrm{5}\right)\left({a}^{\mathrm{2}} −\mathrm{15}{a}+\mathrm{25}\right)=\mathrm{0} \\ $$$${a}=−\mathrm{5}\:{or}\:{a}=\frac{\mathrm{15}\pm\sqrt{\mathrm{225}−\mathrm{100}}}{\mathrm{2}}=\frac{\mathrm{15}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${a}=−\mathrm{5},\:{c}=−\mathrm{5},\:{b}=−\mathrm{5},\:{c}=−\mathrm{5}\:\:\:\:\:\:\:\:....\left(\mathrm{B}\right) \\ $$$${a}=\frac{\mathrm{15}−\sqrt{\mathrm{5}}}{\mathrm{2}},{c}=\frac{\mathrm{25}}{{a}}=\frac{\mathrm{50}}{\mathrm{15}−\sqrt{\mathrm{5}}}=\frac{\mathrm{50}\left(\mathrm{15}+\sqrt{\mathrm{5}}\right)}{\mathrm{100}}=\frac{\mathrm{15}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:{b}=\mathrm{2}{c}−{a}=\frac{\mathrm{15}+\mathrm{15}\sqrt{\mathrm{5}}}{\mathrm{2}},{d}=\frac{\mathrm{15}−\mathrm{15}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:\:\:\:...\left({C}\right) \\ $$$${similar}\:{you}\:{can}\:{get}\:{the}\:{last}\:{solution}\:{for}\:{a}=\frac{\mathrm{15}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${a}=\frac{\mathrm{15}+\sqrt{\mathrm{5}}}{\mathrm{2}},{c}=\frac{\mathrm{15}−\sqrt{\mathrm{5}}}{\mathrm{2}},{b}=\frac{\mathrm{15}−\mathrm{15}\sqrt{\mathrm{5}}}{\mathrm{2}},\:{d}=\frac{\mathrm{15}+\mathrm{15}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:..\left({D}\right) \\ $$$${C}\:\mathrm{ans}\:{D}\:\mathrm{are}\:\mathrm{only}\:\mathrm{valid}\:\mathrm{solutions}\:\mathrm{for} \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\mathrm{are}\:\mathrm{different}. \\ $$$$\mathrm{in}\:\mathrm{both}\:\mathrm{cases} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=\mathrm{30} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com