
Question and Answers Forum
Question Number 28613 by abdo imad last updated on 27/Jan/18
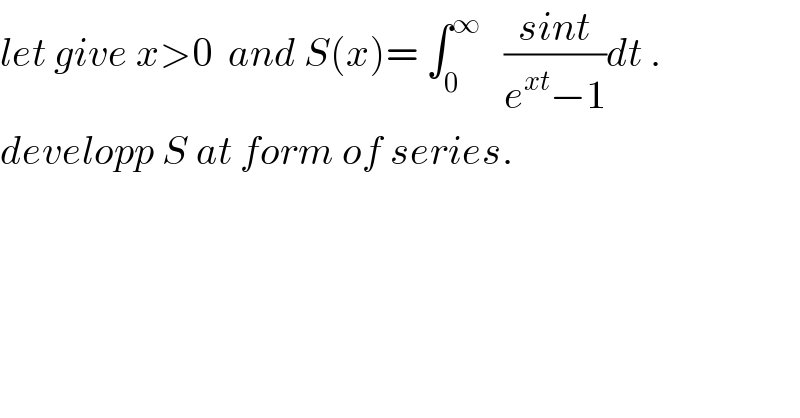
Commented byabdo imad last updated on 01/Feb/18
![S(x)= ∫_0 ^∞ ((e^(−xt) sint)/(1−e^(−xt) ))dt= ∫_0 ^∞ ( Σ_(n=0) ^∞ e^(−nxt) )e^(−xt) sintdt = Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)xt) sint dt=Σ_(n=0) ^∞ A_n (x) A_n (x)= ∫_0 ^∞ e^(−(n+1)xt) sint dt=−Im( ∫_0 ^∞ e^(−((n+1)x +i)t) dt)but ∫_0 ^∞ e^(−((n+1)x+i)t) dt =−(1/((n+1)x+i))[ e^(−((n+1)x+i)t) ]_0 ^(+∞) = (1/((n+1)x+i))=(((n+1)x−i)/((n+1)^2 x^2 +1))=(((n+1)x)/(1+(n+1)^2 x^2 ))−(i/(1+(n+1)^2 x^2 )) A_n (x)= (1/(1+(n+1)^2 x^2 )) ⇒S(x)= Σ_(n=0) ^∞ (1/(1+(n+1)^2 x^2 )) with x>0](Q28944.png)
| ||
Question and Answers Forum | ||
Question Number 28613 by abdo imad last updated on 27/Jan/18 | ||
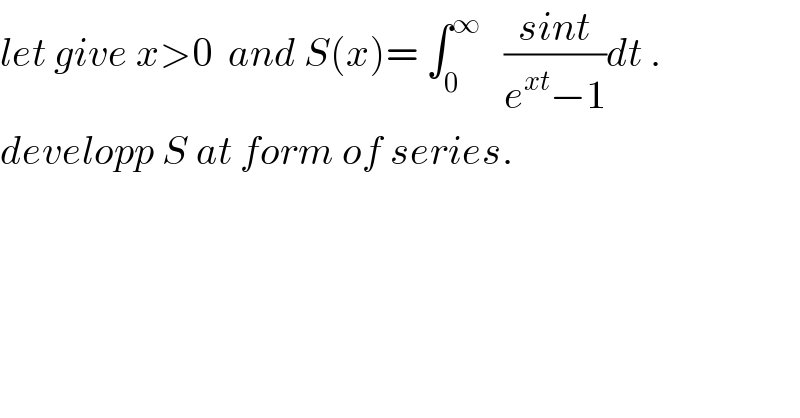 | ||
Commented byabdo imad last updated on 01/Feb/18 | ||
![S(x)= ∫_0 ^∞ ((e^(−xt) sint)/(1−e^(−xt) ))dt= ∫_0 ^∞ ( Σ_(n=0) ^∞ e^(−nxt) )e^(−xt) sintdt = Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)xt) sint dt=Σ_(n=0) ^∞ A_n (x) A_n (x)= ∫_0 ^∞ e^(−(n+1)xt) sint dt=−Im( ∫_0 ^∞ e^(−((n+1)x +i)t) dt)but ∫_0 ^∞ e^(−((n+1)x+i)t) dt =−(1/((n+1)x+i))[ e^(−((n+1)x+i)t) ]_0 ^(+∞) = (1/((n+1)x+i))=(((n+1)x−i)/((n+1)^2 x^2 +1))=(((n+1)x)/(1+(n+1)^2 x^2 ))−(i/(1+(n+1)^2 x^2 )) A_n (x)= (1/(1+(n+1)^2 x^2 )) ⇒S(x)= Σ_(n=0) ^∞ (1/(1+(n+1)^2 x^2 )) with x>0](Q28944.png) | ||