
Question Number 28677 by abdo imad last updated on 28/Jan/18
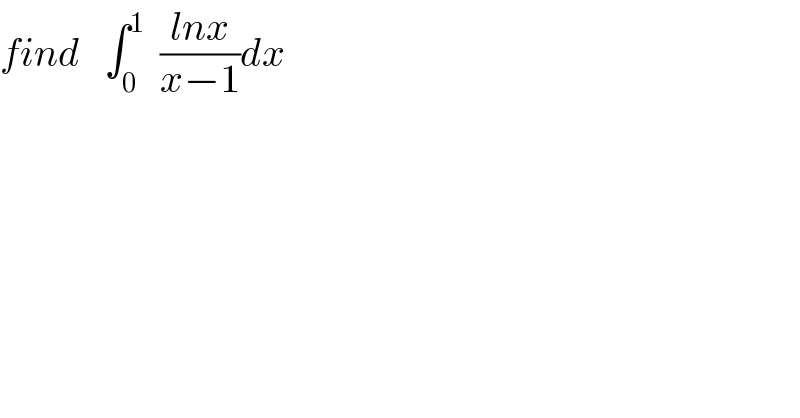
$${find}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{lnx}}{{x}−\mathrm{1}}{dx} \\ $$
Commented by abdo imad last updated on 29/Jan/18
![let put I= ∫_0 ^1 ((lnx)/(x−1))dx I=−∫_0 ^1 ((lnx)/(1−x))dx=− ∫_0 ^1 (Σ_(n=0) ^(+∞) x^n )lnx dx =− Σ_(n=0) ^(+∞) ∫_0 ^1 x^n lnxdx let integrate by parts ∫^1 _0 x^n lnxdx= [ (1/(n+1))x^(n+1) lnx]_(x→0) ^(x=1) − ∫_0 ^1 (1/(n+1)) x^(n+1) (dx/x) =−(1/(n+1)) ∫_0 ^1 x^n dx= −(1/((n+1)^2 )) I= Σ_(n=0) ^(+∞) (1/((n+1)^2 ))= Σ_(n=1) ^(+∞) (1/n^2 )= (π^2 /6) .](Q28753.png)
$${let}\:{put}\:\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{lnx}}{{x}−\mathrm{1}}{dx} \\ $$$${I}=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{lnx}}{\mathrm{1}−{x}}{dx}=−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{+\infty} \:{x}^{{n}} \right){lnx}\:{dx} \\ $$$$=−\:\sum_{{n}=\mathrm{0}} ^{+\infty} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}} {lnxdx}\:\:{let}\:{integrate}\:{by}\:{parts} \\ $$$$\underset{\mathrm{0}} {\int}^{\mathrm{1}} \:{x}^{{n}} {lnxdx}=\:\left[\:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} {lnx}\right]_{{x}\rightarrow\mathrm{0}} ^{{x}=\mathrm{1}} \:\:\:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} \:\frac{{dx}}{{x}} \\ $$$$=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {dx}=\:−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}=\:\sum_{{n}=\mathrm{0}} ^{+\infty} \:\:\:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\:\sum_{{n}=\mathrm{1}} ^{+\infty} \:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:.\:\: \\ $$
