
Question Number 28679 by abdo imad last updated on 28/Jan/18
![f function contnue on [0,1] .prove that lim_(n→+∞) n∫_0 ^1 t^n f(t)dt=f(1).](Q28679.png)
$${f}\:{function}\:{contnue}\:{on}\:\left[\mathrm{0},\mathrm{1}\right]\:.{prove}\:{that} \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:{n}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{{n}} {f}\left({t}\right){dt}={f}\left(\mathrm{1}\right). \\ $$
Commented by abdo imad last updated on 29/Jan/18
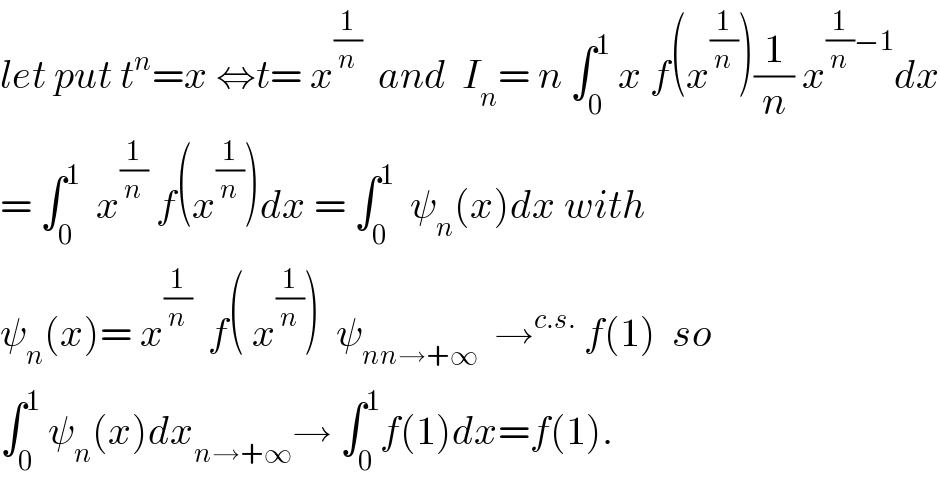
$${let}\:{put}\:{t}^{{n}} ={x}\:\Leftrightarrow{t}=\:{x}^{\frac{\mathrm{1}}{{n}}} \:\:{and}\:\:{I}_{{n}} =\:{n}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{f}\left({x}^{\frac{\mathrm{1}}{{n}}} \right)\frac{\mathrm{1}}{{n}}\:{x}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{\frac{\mathrm{1}}{{n}}} \:{f}\left({x}^{\frac{\mathrm{1}}{{n}}} \right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\psi_{{n}} \left({x}\right){dx}\:{with} \\ $$$$\psi_{{n}} \left({x}\right)=\:{x}^{\frac{\mathrm{1}}{{n}}} \:\:{f}\left(\:{x}^{\frac{\mathrm{1}}{{n}}} \right)\:\:\psi_{{nn}\rightarrow+\infty} \:\:\rightarrow^{{c}.{s}.} \:{f}\left(\mathrm{1}\right)\:\:{so} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\psi_{{n}} \left({x}\right){dx}_{{n}\rightarrow+\infty} \rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left(\mathrm{1}\right){dx}={f}\left(\mathrm{1}\right). \\ $$
