
Question and Answers Forum
Question Number 28683 by abdo imad last updated on 28/Jan/18
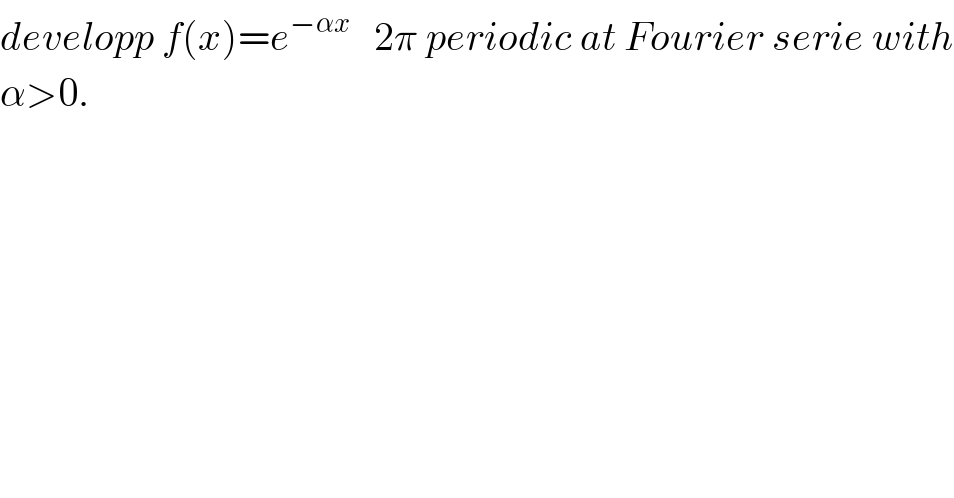
Commented byabdo imad last updated on 31/Jan/18
![f(x)=Σ_(n=−∞) ^(+∞) c_n e^(inx) and c_n = (1/T) ∫_([T]) f(x) e^(−inx) dx =(1/(2π)) ∫_(−π) ^π e^(−αx) e^(−inx) dx ⇒2π c_n = ∫_(−π) ^π e^(−(α+in)x) dx =((−1)/(α+in)) [ e^(−(α+in)x) ]_(−π) ^π =((−1)/(α+in)) ( e^(−(α+in)π) −e^((𝛂+in)π) ) =((−1)/(α+in))( (−1)^n e^(−απ) −(−1)^n e^(απ) ) = (((−1)^n )/(α+in))(e^(απ) −e^(−απ) ) =((2(−1)^n )/(α+in)) sh(απ) ⇒ c_n = ((sh(απ))/π) (((−1)^n )/(α +in)) so f(x)= Σ_(n=−∞) ^(+∞) ((sh(απ))/π) (((−1)^n )/(α+in)) e^(inx) .](Q28880.png)
| ||
Question and Answers Forum | ||
Question Number 28683 by abdo imad last updated on 28/Jan/18 | ||
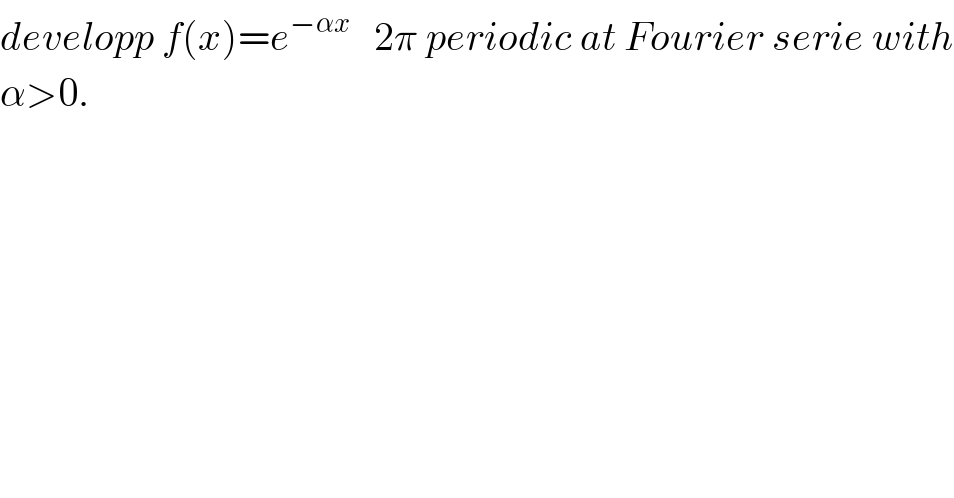 | ||
Commented byabdo imad last updated on 31/Jan/18 | ||
![f(x)=Σ_(n=−∞) ^(+∞) c_n e^(inx) and c_n = (1/T) ∫_([T]) f(x) e^(−inx) dx =(1/(2π)) ∫_(−π) ^π e^(−αx) e^(−inx) dx ⇒2π c_n = ∫_(−π) ^π e^(−(α+in)x) dx =((−1)/(α+in)) [ e^(−(α+in)x) ]_(−π) ^π =((−1)/(α+in)) ( e^(−(α+in)π) −e^((𝛂+in)π) ) =((−1)/(α+in))( (−1)^n e^(−απ) −(−1)^n e^(απ) ) = (((−1)^n )/(α+in))(e^(απ) −e^(−απ) ) =((2(−1)^n )/(α+in)) sh(απ) ⇒ c_n = ((sh(απ))/π) (((−1)^n )/(α +in)) so f(x)= Σ_(n=−∞) ^(+∞) ((sh(απ))/π) (((−1)^n )/(α+in)) e^(inx) .](Q28880.png) | ||