Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2874 by RasheedAhmad last updated on 29/Nov/15

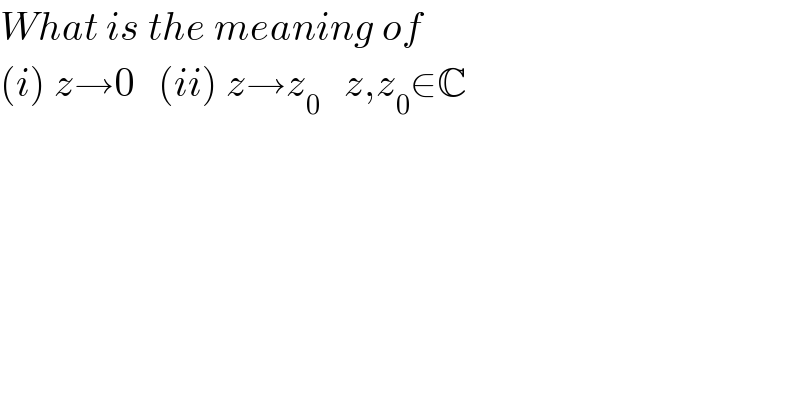
What is the meaning of (i) z→0 (ii) z→z_0 z,z_0 ∈C

$${What}\:{is}\:{the}\:{meaning}\:{of} \\ $$$$\left({i}\right)\:{z}\rightarrow\mathrm{0}\:\:\:\left({ii}\right)\:{z}\rightarrow{z}_{\mathrm{0}} \:\:\:{z},{z}_{\mathrm{0}} \in\mathbb{C} \\ $$

Answered by Filup last updated on 29/Nov/15

(1) z approaches 0 z→0^+ approaches from right side z→0^− approaches from left side e.g. f(x)= { ((x≥0, 1)),((x<0, 2)) :} lim_(x→0^+ ) f(x)=1 lim_(x→0^− ) f(x)=2 (2) z, z_0 ∈C means that both z and z_0 are within the complex set. Simply, they are complex functions. Such as: z=1+2i if z→z_0 , then for complex z, it approaches complex z_0

$$\left(\mathrm{1}\right) \\ $$$${z}\:\mathrm{approaches}\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{z}\rightarrow\mathrm{0}^{+} \:\mathrm{approaches}\:\mathrm{from}\:\mathrm{right}\:\mathrm{side} \\ $$$$\:\:\:\:\:\:\:\:\:{z}\rightarrow\mathrm{0}^{−} \:\mathrm{approaches}\:\mathrm{from}\:\mathrm{left}\:\mathrm{side} \\ $$$$\mathrm{e}.\mathrm{g}. \\ $$$${f}\left({x}\right)=\begin{cases}{{x}\geqslant\mathrm{0},\:\:\mathrm{1}}\\{{x}<\mathrm{0},\:\:\mathrm{2}}\end{cases} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}{f}\left({x}\right)=\mathrm{2} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${z},\:{z}_{\mathrm{0}} \in\mathbb{C}\:\:\mathrm{means}\:\mathrm{that}\:\mathrm{both}\:{z}\:\mathrm{and}\:{z}_{\mathrm{0}} \\ $$$$\mathrm{are}\:\mathrm{within}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{set}.\:\mathrm{Simply}, \\ $$$$\mathrm{they}\:\mathrm{are}\:\mathrm{complex}\:\mathrm{functions}. \\ $$$$\mathrm{Such}\:\mathrm{as}:\:\:\:{z}=\mathrm{1}+\mathrm{2}{i} \\ $$$$ \\ $$$$\mathrm{if}\:\:{z}\rightarrow{z}_{\mathrm{0}} ,\:\mathrm{then}\:\mathrm{for}\:\mathrm{complex}\:{z},\:\mathrm{it}\: \\ $$$$\mathrm{approaches}\:\mathrm{complex}\:{z}_{\mathrm{0}} \\ $$

Answered by Yozzi last updated on 29/Nov/15

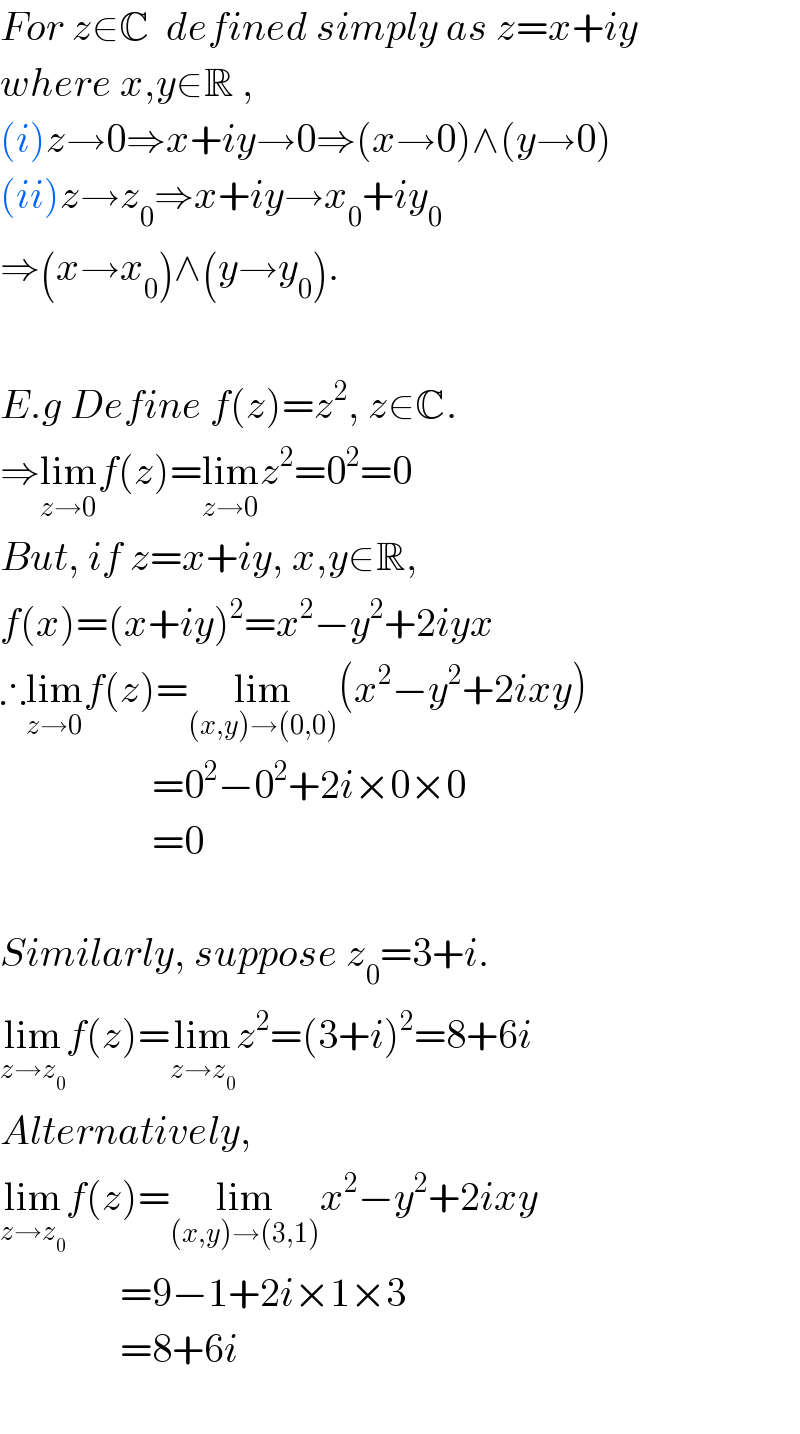
For z∈C defined simply as z=x+iy where x,y∈R , (i)z→0⇒x+iy→0⇒(x→0)∧(y→0) (ii)z→z_0 ⇒x+iy→x_0 +iy_0 ⇒(x→x_0 )∧(y→y_0 ). E.g Define f(z)=z^2 , z∈C. ⇒lim_(z→0) f(z)=lim_(z→0) z^2 =0^2 =0 But, if z=x+iy, x,y∈R, f(x)=(x+iy)^2 =x^2 −y^2 +2iyx ∴lim_(z→0) f(z)=lim_((x,y)→(0,0)) (x^2 −y^2 +2ixy) =0^2 −0^2 +2i×0×0 =0 Similarly, suppose z_0 =3+i. lim_(z→z_0 ) f(z)=lim_(z→z_0 ) z^2 =(3+i)^2 =8+6i Alternatively, lim_(z→z_0 ) f(z)=lim_((x,y)→(3,1)) x^2 −y^2 +2ixy =9−1+2i×1×3 =8+6i

$${For}\:{z}\in\mathbb{C}\:\:{defined}\:{simply}\:{as}\:{z}={x}+{iy} \\ $$$${where}\:{x},{y}\in\mathbb{R}\:, \\ $$$$\left({i}\right){z}\rightarrow\mathrm{0}\Rightarrow{x}+{iy}\rightarrow\mathrm{0}\Rightarrow\left({x}\rightarrow\mathrm{0}\right)\wedge\left({y}\rightarrow\mathrm{0}\right) \\ $$$$\left({ii}\right){z}\rightarrow{z}_{\mathrm{0}} \Rightarrow{x}+{iy}\rightarrow{x}_{\mathrm{0}} +{iy}_{\mathrm{0}} \\ $$$$\Rightarrow\left({x}\rightarrow{x}_{\mathrm{0}} \right)\wedge\left({y}\rightarrow{y}_{\mathrm{0}} \right). \\ $$$$ \\ $$$${E}.{g}\:{Define}\:{f}\left({z}\right)={z}^{\mathrm{2}} ,\:{z}\in\mathbb{C}. \\ $$$$\Rightarrow\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({z}\right)=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}{z}^{\mathrm{2}} =\mathrm{0}^{\mathrm{2}} =\mathrm{0} \\ $$$${But},\:{if}\:{z}={x}+{iy},\:{x},{y}\in\mathbb{R}, \\ $$$${f}\left({x}\right)=\left({x}+{iy}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{iyx} \\ $$$$\therefore\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({z}\right)=\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{ixy}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}^{\mathrm{2}} −\mathrm{0}^{\mathrm{2}} +\mathrm{2}{i}×\mathrm{0}×\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0} \\ $$$$ \\ $$$${Similarly},\:{suppose}\:{z}_{\mathrm{0}} =\mathrm{3}+{i}. \\ $$$$\underset{{z}\rightarrow{z}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({z}\right)=\underset{{z}\rightarrow{z}_{\mathrm{0}} } {\mathrm{lim}}{z}^{\mathrm{2}} =\left(\mathrm{3}+{i}\right)^{\mathrm{2}} =\mathrm{8}+\mathrm{6}{i} \\ $$$${Alternatively}, \\ $$$$\underset{{z}\rightarrow{z}_{\mathrm{0}} } {\mathrm{lim}}{f}\left({z}\right)=\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{3},\mathrm{1}\right)} {\mathrm{lim}}{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{ixy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{9}−\mathrm{1}+\mathrm{2}{i}×\mathrm{1}×\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8}+\mathrm{6}{i} \\ $$$$ \\ $$

Commented by Yozzi last updated on 29/Nov/15

I see. Thanks!

$${I}\:{see}.\:{Thanks}! \\ $$

Commented by 123456 last updated on 29/Nov/15

however there infinite ways to aproach z_0 on C, so if the limit depends on path that you taked, them it doenst exist [like in the R, lim_(x→0^− ) f(x)≠lim_(x→0^+ ) f(x),lim_(x→0) f(x)=∄]

$$\mathrm{however}\:\mathrm{there}\:\mathrm{infinite}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{aproach} \\ $$$${z}_{\mathrm{0}} \:\mathrm{on}\:\mathbb{C},\:\mathrm{so}\:\mathrm{if}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{path} \\ $$$$\mathrm{that}\:\mathrm{you}\:\mathrm{taked},\:\mathrm{them}\:\mathrm{it}\:\mathrm{doenst}\:\mathrm{exist} \\ $$$$\left[\mathrm{like}\:\mathrm{in}\:\mathrm{the}\:\mathbb{R},\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}{f}\left({x}\right)\neq\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}{f}\left({x}\right),\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)=\nexists\right] \\ $$

Commented by prakash jain last updated on 29/Nov/15

The same concept (path dependency applies) when computing limits for functions of more than one variable. for z→0 or z→z_0 limits it is sometimes easier to convert to polar coordinates then consider limit on r with no constraints on θ.

$$\mathrm{The}\:\mathrm{same}\:\mathrm{concept}\:\left(\mathrm{path}\:\mathrm{dependency}\:\mathrm{applies}\right) \\ $$$$\mathrm{when}\:\mathrm{computing}\:\mathrm{limits}\:\mathrm{for}\:\mathrm{functions}\:\mathrm{of} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{one}\:\mathrm{variable}. \\ $$$$\mathrm{for}\:{z}\rightarrow\mathrm{0}\:\mathrm{or}\:{z}\rightarrow{z}_{\mathrm{0}} \:\mathrm{limits}\:\mathrm{it}\:\mathrm{is}\:\mathrm{sometimes}\:\mathrm{easier}\:\mathrm{to} \\ $$$$\mathrm{convert}\:\mathrm{to}\:\mathrm{polar}\:\mathrm{coordinates}\:\mathrm{then}\:\mathrm{consider} \\ $$$$\mathrm{limit}\:\mathrm{on}\:{r}\:\mathrm{with}\:\mathrm{no}\:\mathrm{constraints}\:\mathrm{on}\:\theta. \\ $$

Commented by Rasheed Soomro last updated on 29/Nov/15

What are other ways, for example, of approaching z_0 and what is ′path dependancy′?

$${What}\:{are}\:{other}\:{ways},\:{for}\:{example},\:{of}\:{approaching}\:{z}_{\mathrm{0}} \\ $$$${and}\:{what}\:{is}\:'{path}\:{dependancy}'? \\ $$

Commented by 123456 last updated on 29/Nov/15

lets z_0 =0 we can aproach z by z=te^(ıt) ,t→0^+ (path 1) z=re^(ıθ) ,r→0 (path 2) the first path is a spiral and the second is a stray line with angle θ with real line path depedency=limits depends on the path you take to aproach z_0 in real case with one varriable we have only the paths x→0^+ x→0^− however in C we have infinites path as you see in above a example of two path, there are more paths that you can take.

$$\mathrm{lets}\:{z}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{aproach}\:{z}\:{by} \\ $$$${z}={te}^{\imath{t}} ,{t}\rightarrow\mathrm{0}^{+} \:\left(\mathrm{path}\:\mathrm{1}\right)\:\: \\ $$$${z}={re}^{\imath\theta} ,{r}\rightarrow\mathrm{0}\:\left(\mathrm{path}\:\mathrm{2}\right) \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{path}\:\mathrm{is}\:\mathrm{a}\:\mathrm{spiral}\:\mathrm{and}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{stray}\:\mathrm{line}\:\mathrm{with}\:\mathrm{angle}\:\theta\:\mathrm{with}\:\mathrm{real}\:\mathrm{line} \\ $$$$\mathrm{path}\:\mathrm{depedency}=\mathrm{limits}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{path}\:\mathrm{you}\:\mathrm{take}\:\mathrm{to}\:\mathrm{aproach}\:{z}_{\mathrm{0}} \\ $$$$\mathrm{in}\:\mathrm{real}\:\mathrm{case}\:\mathrm{with}\:\mathrm{one}\:\mathrm{varriable}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{only}\:\mathrm{the}\:\mathrm{paths} \\ $$$${x}\rightarrow\mathrm{0}^{+} \\ $$$${x}\rightarrow\mathrm{0}^{−} \\ $$$$\mathrm{however}\:\mathrm{in}\:\mathbb{C}\:\mathrm{we}\:\mathrm{have}\:\mathrm{infinites}\:\mathrm{path} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{see}\:\mathrm{in}\:\mathrm{above}\:\mathrm{a}\:\mathrm{example}\:\mathrm{of}\:\mathrm{two} \\ $$$$\mathrm{path},\:\mathrm{there}\:\mathrm{are}\:\mathrm{more}\:\mathrm{paths}\:\mathrm{that}\:\mathrm{you} \\ $$$$\mathrm{can}\:\mathrm{take}. \\ $$

Commented by Rasheed Soomro last updated on 29/Nov/15

T HANK^(Sss) for all of YOU ! I always have learnt from you.

$$\mathcal{T}\:\mathcal{HANK}^{\mathcal{S}\boldsymbol{{s}}{s}} \:\boldsymbol{{for}}\:\boldsymbol{{all}}\:\boldsymbol{{of}}\:\boldsymbol{\mathcal{Y}}\mathcal{OU}\:! \\ $$$$\mathcal{I}\:{always}\:{have}\:{learnt}\:{from}\:{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com