Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 2878 by Yozzi last updated on 29/Nov/15

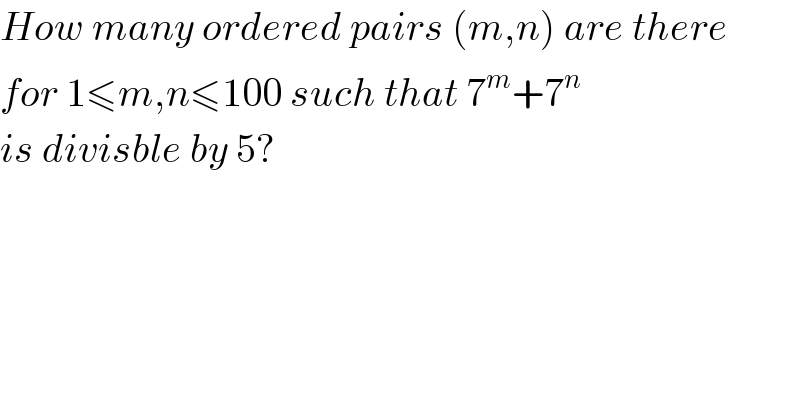
How many ordered pairs (m,n) are there for 1≤m,n≤100 such that 7^m +7^n is divisble by 5?

$${How}\:{many}\:{ordered}\:{pairs}\:\left({m},{n}\right)\:{are}\:{there} \\ $$$${for}\:\mathrm{1}\leqslant{m},{n}\leqslant\mathrm{100}\:{such}\:{that}\:\mathrm{7}^{{m}} +\mathrm{7}^{{n}} \\ $$$${is}\:{divisble}\:{by}\:\mathrm{5}? \\ $$

Commented by prakash jain last updated on 29/Nov/15

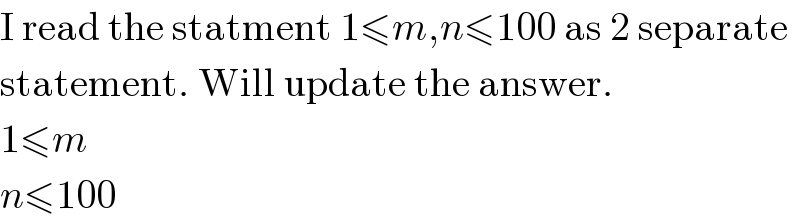
I read the statment 1≤m,n≤100 as 2 separate statement. Will update the answer. 1≤m n≤100

$$\mathrm{I}\:\mathrm{read}\:\mathrm{the}\:\mathrm{statment}\:\mathrm{1}\leqslant{m},{n}\leqslant\mathrm{100}\:\mathrm{as}\:\mathrm{2}\:\mathrm{separate} \\ $$$$\mathrm{statement}.\:\mathrm{Will}\:\mathrm{update}\:\mathrm{the}\:\mathrm{answer}. \\ $$$$\mathrm{1}\leqslant{m} \\ $$$${n}\leqslant\mathrm{100} \\ $$

Answered by prakash jain last updated on 29/Nov/15

7^m +7^n ≡0 (mod 5) 2^m +2^n ≡0 (mod 5) k∈{0,1,2,3} k=4j⇒2^k ≡1 (mod 5) k=4j+1⇒2^k ≡2 (mod 5) k=4j+2⇒2^k ≡4 (mod 5) k=4j+3⇒2^k ≡3 (mod 5) Solution for m and n j,l∈{0,1,2,3} m=4j, n=4l+2 m=4j+1, n=4l+3 m=4j+2, n=4l m=4j+3, n=4l+1 1≤n≤100, 1≤m≤100 n=4l 1≤l≤25 m=4j+2 0≤j≤24 n=4l+1 0≤l≤24 m=4j+3, 0≤j≤24 n=4l+2 0≤l≤24 m=4j 1≤j≤25 n=4l+3 0≤l≤24 m=4j+1 0≤j≤24 Total number of pairs=4×25^2 =625×4=2500

$$\mathrm{7}^{{m}} +\mathrm{7}^{{n}} \equiv\mathrm{0}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$$\mathrm{2}^{{m}} +\mathrm{2}^{{n}} \equiv\mathrm{0}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$${k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$${k}=\mathrm{4}{j}\Rightarrow\mathrm{2}^{{k}} \equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$${k}=\mathrm{4}{j}+\mathrm{1}\Rightarrow\mathrm{2}^{{k}} \equiv\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$${k}=\mathrm{4}{j}+\mathrm{2}\Rightarrow\mathrm{2}^{{k}} \equiv\mathrm{4}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$${k}=\mathrm{4}{j}+\mathrm{3}\Rightarrow\mathrm{2}^{{k}} \equiv\mathrm{3}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$$\mathrm{Solution}\:\mathrm{for}\:{m}\:\mathrm{and}\:{n} \\ $$$${j},{l}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$${m}=\mathrm{4}{j},\:{n}=\mathrm{4}{l}+\mathrm{2} \\ $$$${m}=\mathrm{4}{j}+\mathrm{1},\:{n}=\mathrm{4}{l}+\mathrm{3} \\ $$$${m}=\mathrm{4}{j}+\mathrm{2},\:{n}=\mathrm{4}{l} \\ $$$${m}=\mathrm{4}{j}+\mathrm{3},\:{n}=\mathrm{4}{l}+\mathrm{1} \\ $$$$\mathrm{1}\leqslant{n}\leqslant\mathrm{100},\:\mathrm{1}\leqslant{m}\leqslant\mathrm{100} \\ $$$${n}=\mathrm{4}{l}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\leqslant{l}\leqslant\mathrm{25}\: \\ $$$$\:\:\:{m}=\mathrm{4}{j}+\mathrm{2}\:\:\:\:\:\:\mathrm{0}\leqslant{j}\leqslant\mathrm{24} \\ $$$${n}=\mathrm{4}{l}+\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant{l}\leqslant\mathrm{24} \\ $$$$\:\:\:{m}=\mathrm{4}{j}+\mathrm{3},\:\:\:\:\:\mathrm{0}\leqslant{j}\leqslant\mathrm{24} \\ $$$${n}=\mathrm{4}{l}+\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant{l}\leqslant\mathrm{24} \\ $$$$\:\:\:{m}=\mathrm{4}{j}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\leqslant{j}\leqslant\mathrm{25} \\ $$$${n}=\mathrm{4}{l}+\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant{l}\leqslant\mathrm{24} \\ $$$$\:\:\:{m}=\mathrm{4}{j}+\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}\leqslant{j}\leqslant\mathrm{24} \\ $$$$\mathrm{Total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{pairs}=\mathrm{4}×\mathrm{25}^{\mathrm{2}} =\mathrm{625}×\mathrm{4}=\mathrm{2500} \\ $$

Answered by Rasheed Soomro last updated on 30/Nov/15

Let 7^m ≡r(mod 5) Experimenting and Observing for values of m and r: 7^((0,1,2,3,4,5,6,...)) ≡(1,2,4,3,1,2,4,...) (mod 5) Generalizing: 7^(4k) ≡1(mod 5) ∥ 7^(4h+2) ≡4(mod 5) 7^(4k+1) ≡2(mod 5) ∥ 7^(4h+3) ≡3(mod 5) 7^(4k+2) ≡4(mod 5) ∥ 7^(4h) ≡1(mod 5) 7^(4k+3) ≡3(mod 5) ∥ 7^(4h+1) ≡2(mod 5) Adding corresponding 7^(4k) +7^(4h+2) ≡0(mod 5) 7^(4k+1) +7^(4h+3) ≡0(mod 5) 7^(4k+2) +7^(4h) ≡0(mod 5) 7^(4k+3) +7^(4h+1) ≡0(mod 5) Four types of ordered pairs [(m,n)] satisfying the given statement. 1≤(4k,4h+2)≤100 1≤(4k+1,4h+3)≤100 1≤(4k+2,4h)≤100 1≤(4k+3,4h+1)≤100 Now it′s easy to count Suppose there are x 4k+1 type numbers between 1 and 100 inclusive and y 4h+3 type numbers between 1 and 100 inclusive THEN There are xy ordered pairs of such numbers. A multiplicational table is easy way of recording and counting all required (m,n)′s

$$ \\ $$$${Let}\:\mathrm{7}^{{m}} \equiv{r}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathcal{E}{xperimenting}\:{and}\:\mathcal{O}{bserving}\:{for}\:{values}\:{of}\:{m}\:{and}\:{r}: \\ $$$$\:\:\:\:\:\:\mathrm{7}^{\left(\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},...\right)} \equiv\left(\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{3},\mathrm{1},\mathrm{2},\mathrm{4},...\right)\:\left({mod}\:\mathrm{5}\right) \\ $$$$\mathcal{G}{eneralizing}: \\ $$$$\mathrm{7}^{\mathrm{4}{k}} \equiv\mathrm{1}\left({mod}\:\mathrm{5}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\parallel\:\:\:\:\:\:\:\:\mathrm{7}^{\mathrm{4}{h}+\mathrm{2}} \equiv\mathrm{4}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathrm{7}^{\mathrm{4}{k}+\mathrm{1}} \equiv\mathrm{2}\left({mod}\:\mathrm{5}\right)\:\:\:\:\:\:\:\:\parallel\:\:\:\:\:\:\:\:\:\mathrm{7}^{\mathrm{4}{h}+\mathrm{3}} \equiv\mathrm{3}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathrm{7}^{\mathrm{4}{k}+\mathrm{2}} \equiv\mathrm{4}\left({mod}\:\mathrm{5}\right)\:\:\:\:\:\:\:\:\parallel\:\:\:\:\:\:\:\:\:\mathrm{7}^{\mathrm{4}{h}} \equiv\mathrm{1}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathrm{7}^{\mathrm{4}{k}+\mathrm{3}} \equiv\mathrm{3}\left({mod}\:\mathrm{5}\right)\:\:\:\:\:\:\:\:\parallel\:\:\:\:\:\:\:\:\:\:\mathrm{7}^{\mathrm{4}{h}+\mathrm{1}} \equiv\mathrm{2}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathcal{A}{dding}\:{corresponding} \\ $$$$\mathrm{7}^{\mathrm{4}{k}} +\mathrm{7}^{\mathrm{4}{h}+\mathrm{2}} \equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathrm{7}^{\mathrm{4}{k}+\mathrm{1}} +\mathrm{7}^{\mathrm{4}{h}+\mathrm{3}} \equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathrm{7}^{\mathrm{4}{k}+\mathrm{2}} +\mathrm{7}^{\mathrm{4}{h}} \equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathrm{7}^{\mathrm{4}{k}+\mathrm{3}} +\mathrm{7}^{\mathrm{4}{h}+\mathrm{1}} \equiv\mathrm{0}\left({mod}\:\mathrm{5}\right) \\ $$$$\mathcal{F}{our}\:{types}\:\:{of}\:{ordered}\:{pairs}\:\left[\left({m},{n}\right)\right]\:{satisfying}\:{the} \\ $$$${given}\:{statement}. \\ $$$$\mathrm{1}\leqslant\left(\mathrm{4}{k},\mathrm{4}{h}+\mathrm{2}\right)\leqslant\mathrm{100} \\ $$$$\mathrm{1}\leqslant\left(\mathrm{4}{k}+\mathrm{1},\mathrm{4}{h}+\mathrm{3}\right)\leqslant\mathrm{100} \\ $$$$\mathrm{1}\leqslant\left(\mathrm{4}{k}+\mathrm{2},\mathrm{4}{h}\right)\leqslant\mathrm{100} \\ $$$$\mathrm{1}\leqslant\left(\mathrm{4}{k}+\mathrm{3},\mathrm{4}{h}+\mathrm{1}\right)\leqslant\mathrm{100} \\ $$$$\mathcal{N}{ow}\:{it}'{s}\:{easy}\:{to}\:{count} \\ $$$$\mathcal{S}{uppose}\:{there}\:{are}\:{x}\:\mathrm{4}{k}+\mathrm{1}\:{type}\:{numbers}\:{between}\:\mathrm{1}\:{and} \\ $$$$\mathrm{100}\:{inclusive}\:{and}\:\:{y}\:\mathrm{4}{h}+\mathrm{3}\:{type}\:{numbers}\:{between}\:\mathrm{1}\:{and} \\ $$$$\mathrm{100}\:{inclusive}\:\mathcal{THEN}\:\: \\ $$$$\:\:\:\:\:\:\:\:{There}\:{are}\:{xy}\:{ordered}\:{pairs}\:{of}\:{such}\:{numbers}. \\ $$$${A}\:{multiplicational}\:{table}\:\:{is}\:{easy}\:{way}\:{of}\:{recording}\:{and} \\ $$$${counting}\:{all}\:{required}\:\left({m},{n}\right)'{s} \\ $$$$ \\ $$

Commented by prakash jain last updated on 29/Nov/15

Thanks. I thought 1≤m n≤100

$$\mathrm{Thanks}. \\ $$$$\mathrm{I}\:\mathrm{thought} \\ $$$$\mathrm{1}\leqslant{m} \\ $$$${n}\leqslant\mathrm{100} \\ $$

Commented by Rasheed Soomro last updated on 29/Nov/15

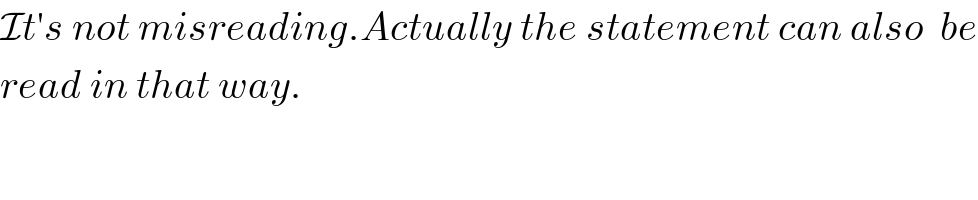
It′s not misreading.Actually the statement can also be read in that way.

$$\mathcal{I}{t}'{s}\:{not}\:{misreading}.{Actually}\:{the}\:{statement}\:{can}\:{also}\:\:{be} \\ $$$${read}\:{in}\:{that}\:{way}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com