
Question and Answers Forum
Question Number 28815 by abdo imad last updated on 30/Jan/18
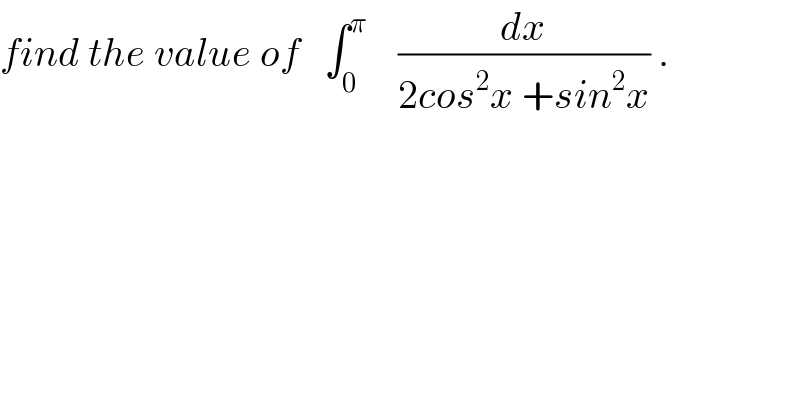
Answered by mrW2 last updated on 31/Jan/18
![∫_0 ^π (dx/(2cos^2 x +sin^2 x)) =∫_0 ^π (dx/(1+cos^2 x)) =2∫_0 ^π (dx/(3+2cos^2 x−1)) =2∫_0 ^π (dx/(3+cos 2x)) =2×2[((tan^(−1) (((tan x)/(√2))))/(2(√2)))]_0 ^(π/2) =(π/(√2))](Q28843.png)
Commented by abdo imad last updated on 31/Jan/18
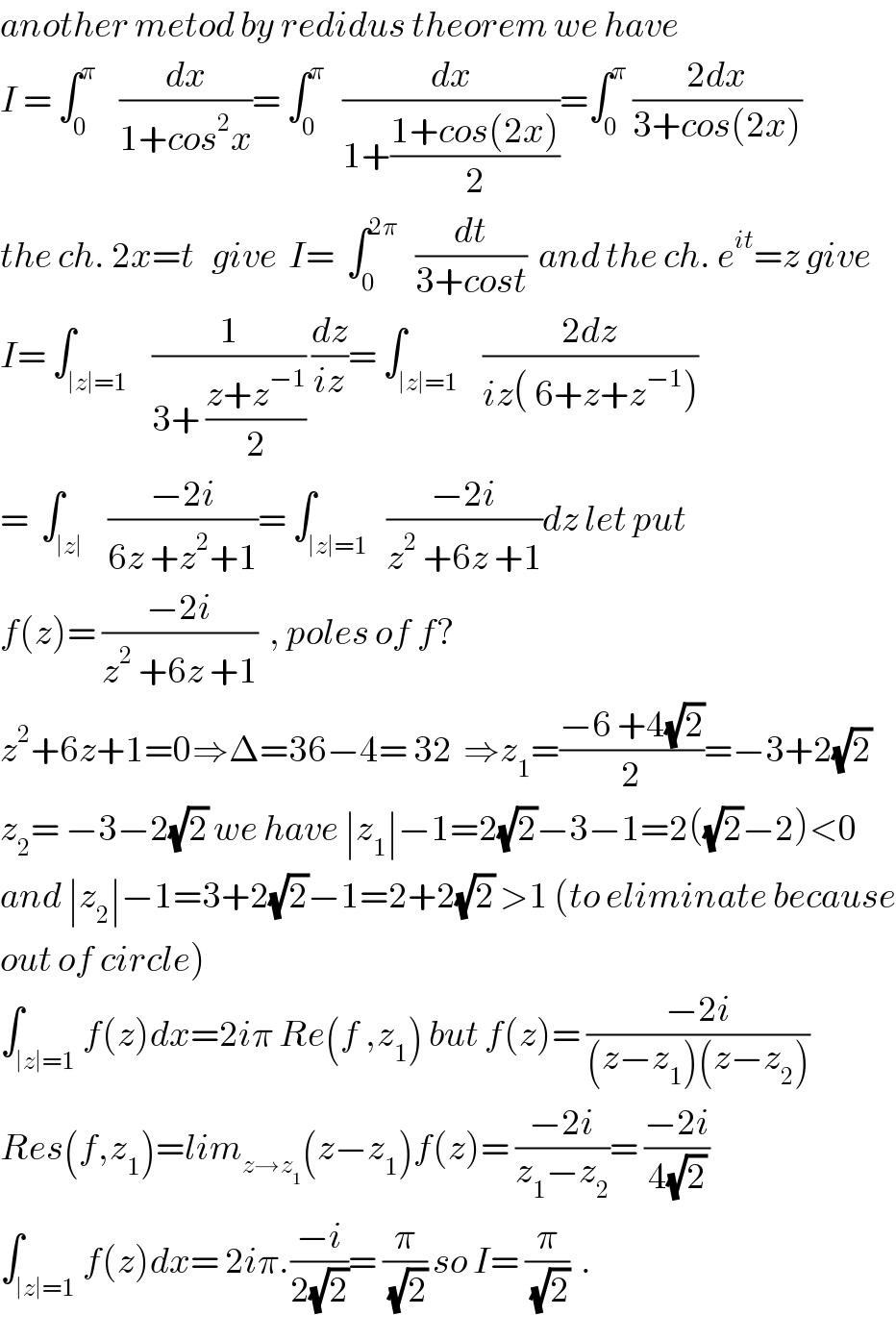
| ||
Question and Answers Forum | ||
Question Number 28815 by abdo imad last updated on 30/Jan/18 | ||
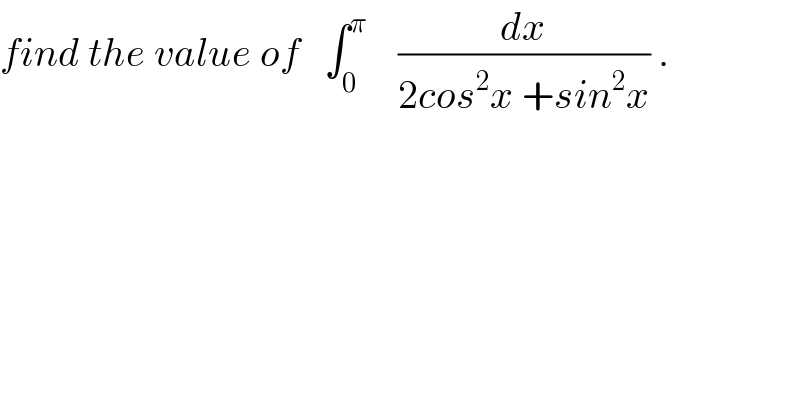 | ||
Answered by mrW2 last updated on 31/Jan/18 | ||
![∫_0 ^π (dx/(2cos^2 x +sin^2 x)) =∫_0 ^π (dx/(1+cos^2 x)) =2∫_0 ^π (dx/(3+2cos^2 x−1)) =2∫_0 ^π (dx/(3+cos 2x)) =2×2[((tan^(−1) (((tan x)/(√2))))/(2(√2)))]_0 ^(π/2) =(π/(√2))](Q28843.png) | ||
| ||
Commented by abdo imad last updated on 31/Jan/18 | ||
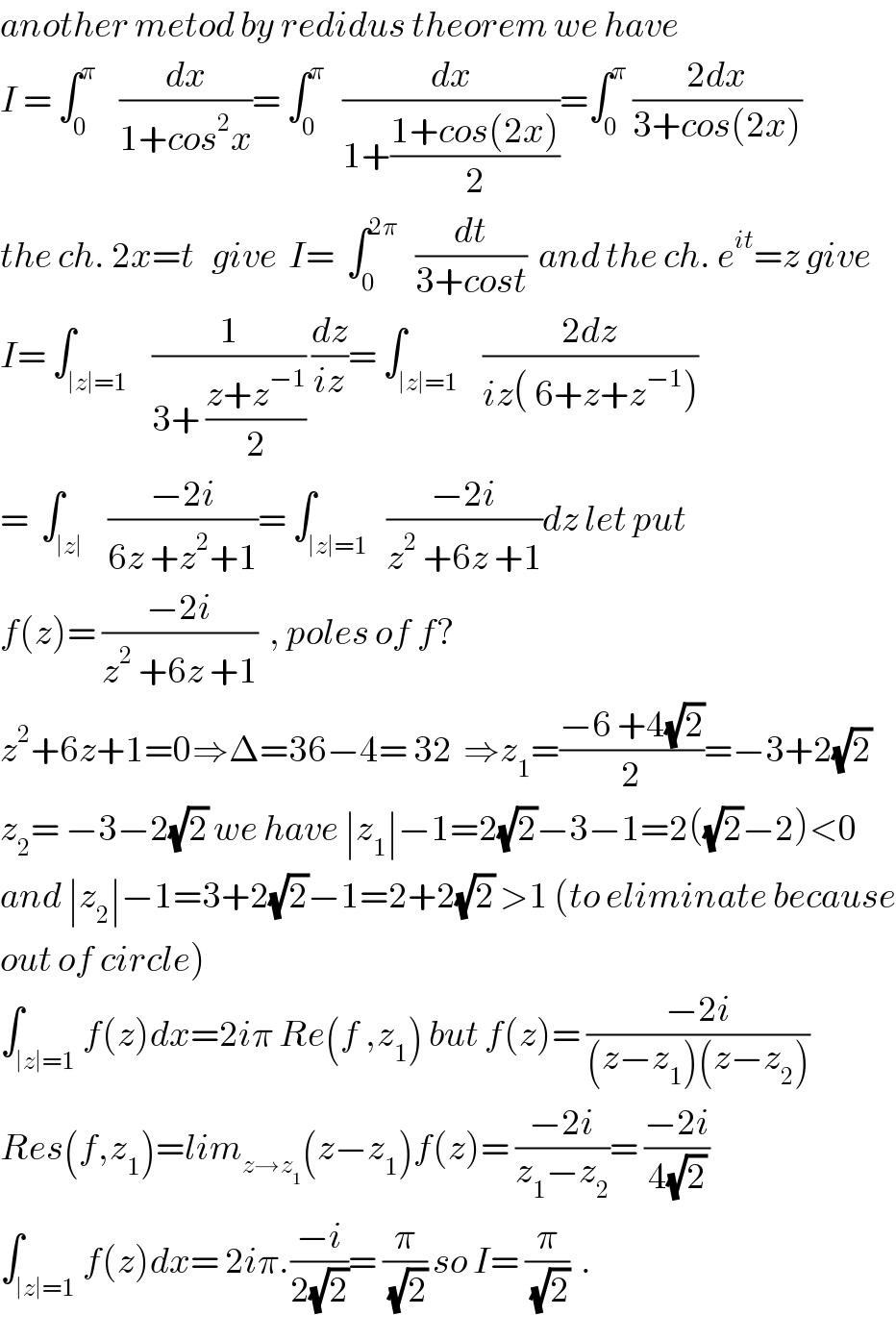 | ||