
Question and Answers Forum
Question Number 28889 by abdo imad last updated on 31/Jan/18
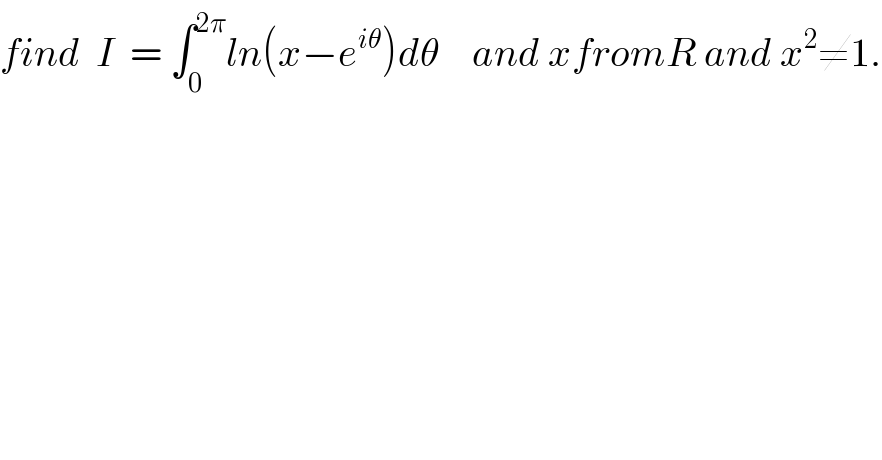
Commented by abdo imad last updated on 02/Feb/18
![let put f(x)= ∫_0 ^(2π) ln(x −e^(iθ) )dθ we have f^′ (x)= ∫_0 ^(2π) (dθ/( x−e^(iθ) ))= ∫_0 ^(2π) (dθ/(x −cosθ −isinθ)) = ∫_0 ^(2π) ((x−cosθ +i sinθ)/((x−cosθ)^2 +sin^2 θ))dθ =∫_0 ^(2π) ((x−cosθ)/(x^2 −2xcosθ +1))dθ +i∫_0 ^(2π) ((sinθ)/(x^2 −2xcosθ +1))dθ =A(x) +iB(x) A(x)=(1/2) ∫_0 ^(2π) ((2x−2cosθ)/(x^2 −2xcosθ+1))dθ=(1/2)[ln∣x^2 −2xcosθ+1∣]_(θ=0) ^(2π) =0 let find B(x) the ch. e^(iθ) =z give B(x)=∫_(∣z∣=1) (((z−z^(−1) )/(2i))/(x^2 −2x((z+z^(−1) )/2) +1))(dz/(iz)) = ∫_(∣z∣=1) ((z−z^(−1) )/(2i( x^2 −2x((z+z^(−1) )/2)+1)iz))dz =∫_(∣z∣=1) ((z^(−1) −z)/(z(2x^2 −2xz −2xz^(−1) +2)))dz = ∫_(∣z∣=1) (((1/z)−z)/(2(x^2 z−xz^2 −x +z)))dz =∫_(∣z∣=1) ((1−z^2 )/(2z( −xz^2 +(1+x^2 )z −x)))dz =∫_(∣z∣=1) ((z^2 −1)/(2z( xz^2 −(1+x^2 )z +x)))dz let introduce the complex function ψ(z)= ((z^2 −1)/(2z( xz^2 −(1+x^2 )z +x))) poles ofψ? xz^2 −(1+x^2 )z +x=0⇒Δ=(1+x^2 )^2 −4x^2 =1+2x^2 +x^4 −4x^2 =(1−x^2 )^2 ⇒z_(1 ) =((1+x^2 +∣1−x^2 ∣)/(2x)) and z_2 =((1+x^2 −∣1−x^2 ∣)/(2x)) (x≠0) case 1 if ∣x∣<1 ⇒z_1 = (1/x) and z_2 =x and we have∣z_1 ∣>1and ∣z_2 ∣<1 ψ(z)= ((z^2 −1)/(2xz(z−z_1 )(z−z_2 ))) and by residus theorem ∫_(∣z∣=1) ψ(z)dz=2iπ(Res(ψ,0) +Res(ψ,z_2 )) Res(ψ,0)=lim_(z→0) zψ(z)= ((−1)/(2x z_1 .z_2 ))=((−1)/(2x)) Res(ψ,z_2 )=lim_(z→z_2 ) (z−z_2 )ψ(z)= ((z_2 ^2 −1)/(2xz_2 (z_2 −z_1 ))) = ((x^2 −1)/(2x^2 (x−(1/x))))=((x^2 −1)/(2x(x^2 −1)))= (1/(2x)) ∫_(∣z∣=1) ψ(z)dz=2iπ(0)=0 case 2 if ∣x∣>1⇒ z_1 = x and z_2 =(1/x) and ∣z_1 ∣>1 and ∣z_2 ∣<1 ∫_(∣z∣=1) ψ(z)dz=2iπ( Res(ψ,0)+Res(ψ,z_2 )) Res(ψ,0)= ((−1)/(2x )) and Res(ψ,z_2 )=((z_2 ^2 −1)/(2xz_2 (z_2 −z_1 ))) =(((1/x^2 )−1)/(2((1/x)−x)))= ((1−x^2 )/(2x^2 ((1−x^2 )/x))) = (1/(2x)) and ∫_(∣z∣=1) ψ(z)dz=0so A(x)=B(x)=0⇒f^′ (x)=0 ⇒f(x)=λ ∀ x /x^2 ≠1](Q28945.png)
Commented by abdo imad last updated on 02/Feb/18
![λ=f(0)=∫_0 ^(2π) ln(−e^(iθ) )dθ = ∫_0 ^(2π) ln(e^(i(π+θ)) )dθ =∫_0 ^(2π) i(π+θ)dθ=2iπ^2 +i[(θ^2 /2)]_0 ^(2π) =2iπ^2 +2iπ^2 =4iπ^2 .](Q28946.png)
Commented by abdo imad last updated on 02/Feb/18
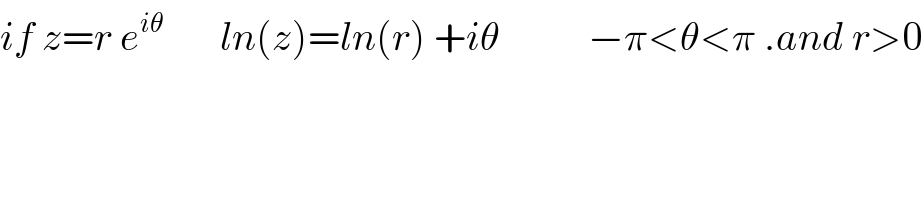
| ||
Question and Answers Forum | ||
Question Number 28889 by abdo imad last updated on 31/Jan/18 | ||
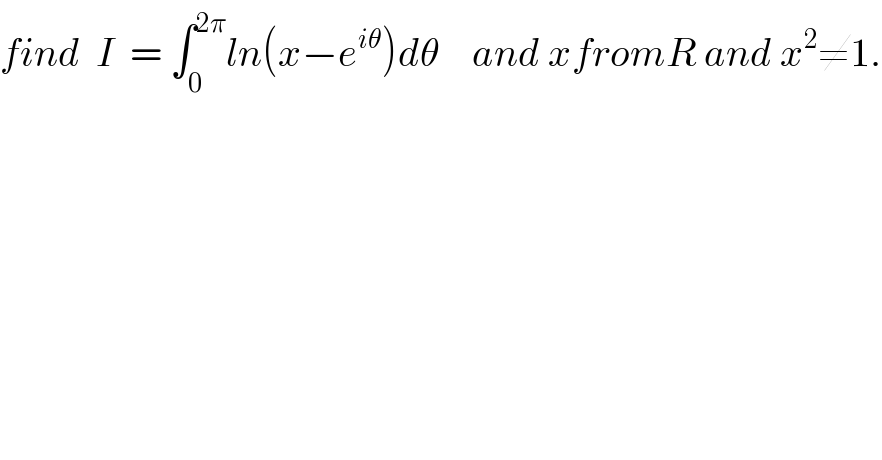 | ||
Commented by abdo imad last updated on 02/Feb/18 | ||
![let put f(x)= ∫_0 ^(2π) ln(x −e^(iθ) )dθ we have f^′ (x)= ∫_0 ^(2π) (dθ/( x−e^(iθ) ))= ∫_0 ^(2π) (dθ/(x −cosθ −isinθ)) = ∫_0 ^(2π) ((x−cosθ +i sinθ)/((x−cosθ)^2 +sin^2 θ))dθ =∫_0 ^(2π) ((x−cosθ)/(x^2 −2xcosθ +1))dθ +i∫_0 ^(2π) ((sinθ)/(x^2 −2xcosθ +1))dθ =A(x) +iB(x) A(x)=(1/2) ∫_0 ^(2π) ((2x−2cosθ)/(x^2 −2xcosθ+1))dθ=(1/2)[ln∣x^2 −2xcosθ+1∣]_(θ=0) ^(2π) =0 let find B(x) the ch. e^(iθ) =z give B(x)=∫_(∣z∣=1) (((z−z^(−1) )/(2i))/(x^2 −2x((z+z^(−1) )/2) +1))(dz/(iz)) = ∫_(∣z∣=1) ((z−z^(−1) )/(2i( x^2 −2x((z+z^(−1) )/2)+1)iz))dz =∫_(∣z∣=1) ((z^(−1) −z)/(z(2x^2 −2xz −2xz^(−1) +2)))dz = ∫_(∣z∣=1) (((1/z)−z)/(2(x^2 z−xz^2 −x +z)))dz =∫_(∣z∣=1) ((1−z^2 )/(2z( −xz^2 +(1+x^2 )z −x)))dz =∫_(∣z∣=1) ((z^2 −1)/(2z( xz^2 −(1+x^2 )z +x)))dz let introduce the complex function ψ(z)= ((z^2 −1)/(2z( xz^2 −(1+x^2 )z +x))) poles ofψ? xz^2 −(1+x^2 )z +x=0⇒Δ=(1+x^2 )^2 −4x^2 =1+2x^2 +x^4 −4x^2 =(1−x^2 )^2 ⇒z_(1 ) =((1+x^2 +∣1−x^2 ∣)/(2x)) and z_2 =((1+x^2 −∣1−x^2 ∣)/(2x)) (x≠0) case 1 if ∣x∣<1 ⇒z_1 = (1/x) and z_2 =x and we have∣z_1 ∣>1and ∣z_2 ∣<1 ψ(z)= ((z^2 −1)/(2xz(z−z_1 )(z−z_2 ))) and by residus theorem ∫_(∣z∣=1) ψ(z)dz=2iπ(Res(ψ,0) +Res(ψ,z_2 )) Res(ψ,0)=lim_(z→0) zψ(z)= ((−1)/(2x z_1 .z_2 ))=((−1)/(2x)) Res(ψ,z_2 )=lim_(z→z_2 ) (z−z_2 )ψ(z)= ((z_2 ^2 −1)/(2xz_2 (z_2 −z_1 ))) = ((x^2 −1)/(2x^2 (x−(1/x))))=((x^2 −1)/(2x(x^2 −1)))= (1/(2x)) ∫_(∣z∣=1) ψ(z)dz=2iπ(0)=0 case 2 if ∣x∣>1⇒ z_1 = x and z_2 =(1/x) and ∣z_1 ∣>1 and ∣z_2 ∣<1 ∫_(∣z∣=1) ψ(z)dz=2iπ( Res(ψ,0)+Res(ψ,z_2 )) Res(ψ,0)= ((−1)/(2x )) and Res(ψ,z_2 )=((z_2 ^2 −1)/(2xz_2 (z_2 −z_1 ))) =(((1/x^2 )−1)/(2((1/x)−x)))= ((1−x^2 )/(2x^2 ((1−x^2 )/x))) = (1/(2x)) and ∫_(∣z∣=1) ψ(z)dz=0so A(x)=B(x)=0⇒f^′ (x)=0 ⇒f(x)=λ ∀ x /x^2 ≠1](Q28945.png) | ||
Commented by abdo imad last updated on 02/Feb/18 | ||
![λ=f(0)=∫_0 ^(2π) ln(−e^(iθ) )dθ = ∫_0 ^(2π) ln(e^(i(π+θ)) )dθ =∫_0 ^(2π) i(π+θ)dθ=2iπ^2 +i[(θ^2 /2)]_0 ^(2π) =2iπ^2 +2iπ^2 =4iπ^2 .](Q28946.png) | ||
Commented by abdo imad last updated on 02/Feb/18 | ||
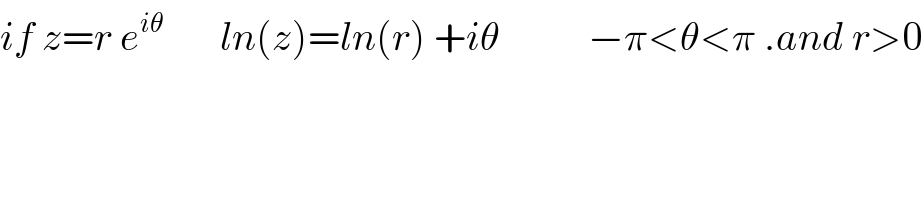 | ||