
Question and Answers Forum
Question Number 28894 by amit96 last updated on 01/Feb/18

Commented by abdo imad last updated on 01/Feb/18
![let put f(x)=F(x,y)= ∫_0 ^(x^2 +y^2 ) cos^2 (t+x)dt we have by ch. t+x=u ⇒f(x)= ∫_x ^(x^2 +y^2 +x) cos^2 udu =∫_x ^(x^2 +y^2 +x) ((1+cos(2u))/2)du =(1/2)(x^2 +y^2 ) +[(1/4)sin(2u)]_x ^(x^2 +y^2 +x) =(1/2)(x^2 +y^2 ) +(1/4)(sin(2x^2 +2y^2 +2x)−sin(2x)) (∂F/∂x)(x,y)=x +(1/4)( (4x+2)cos(2x^2 +2y^2 +2x)−2cos(2x)) (∂F/∂x)(0,y)= (1/4)( 2cos(2y^2 )−2)=(1/2)cos(2y^2 )−(1/2) and any answer given is correct.!](Q28906.png)
Commented by abdo imad last updated on 01/Feb/18
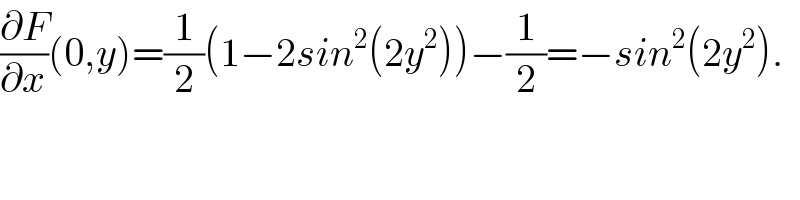
Commented by mrW2 last updated on 01/Feb/18
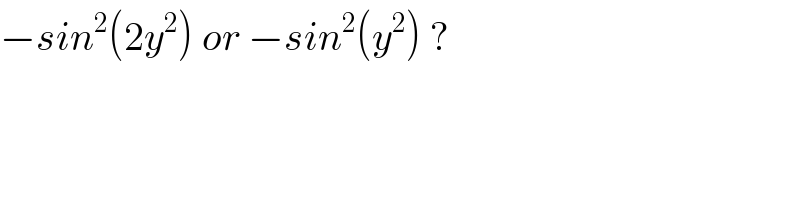
Commented by amit96 last updated on 01/Feb/18
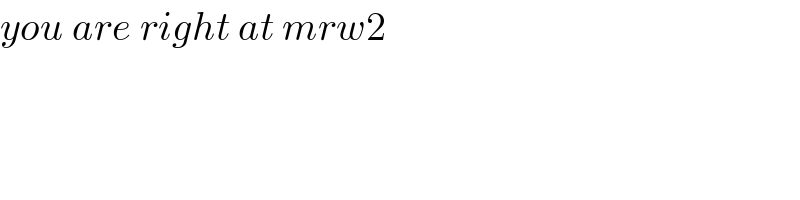
Commented by mrW2 last updated on 01/Feb/18
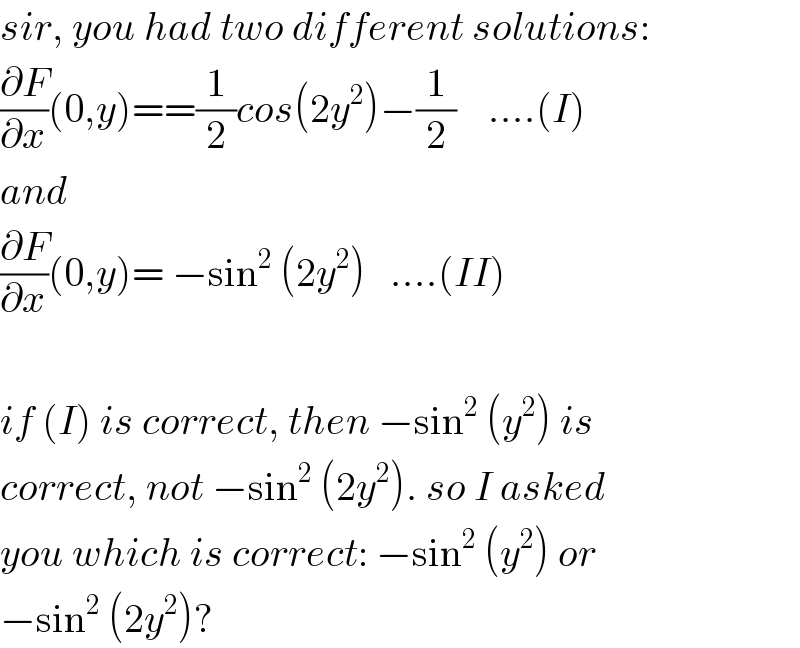
Answered by mrW2 last updated on 01/Feb/18
![∫cos^2 t dt=(1/2)∫(1+cos 2t)dt=(t/2)+((sin 2t)/4)+C F(x,y)=∫_0 ^( x^2 +y^2 ) cos^2 (t+x)dt =[((t+x)/2)+((sin 2(t+x))/4)]_0 ^(x^2 +y^2 ) =[((x^2 +y^2 +x)/2)−(x/2)+((sin 2(x^2 +y^2 +x))/4)−((sin 2x)/4)] =[((x^2 +y^2 )/2)+((sin 2(x^2 +y^2 +x))/4)−((sin 2x)/4)] (∂F/∂x)=x+((cos 2(x^2 +y^2 +x)×2(2x+1))/4)−((cos 2x)/4)×2 (∂F/∂x)=x+(((2x+1) cos 2(x^2 +y^2 +x))/2)−((cos 2x)/2) (∂F/∂x)(0,y)=((cos 2(y^2 ))/2)−(1/2)=((1−2 sin^2 y^2 )/2)−(1/2)=−sin^2 y^2 ⇒none of the answers is correct.](Q28896.png)
Commented by amit96 last updated on 01/Feb/18

