Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 2891 by 123456 last updated on 29/Nov/15

given Γ(z)=lim_(n→+∞) ((n!)/(z(z+1)∙∙∙(z+n)))n^z proof that i) Γ(z+1)=zΓ(z) ii) wiertrass definition of gamma function (1/(Γ(z)))=ze^(zγ) Π_(m=1) ^(+∞) (1+(z/m))e^(−(z/m)) γ is euler macheroni constant (Q2818,Q2783)

$$\mathrm{given} \\ $$$$\Gamma\left({z}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{{n}!}{{z}\left({z}+\mathrm{1}\right)\centerdot\centerdot\centerdot\left({z}+{n}\right)}{n}^{{z}} \\ $$$$\mathrm{proof}\:\mathrm{that} \\ $$$$\left.{i}\right) \\ $$$$\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right) \\ $$$$\left.{ii}\right)\:\mathrm{wiertrass}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{gamma}\:\mathrm{function} \\ $$$$\frac{\mathrm{1}}{\Gamma\left({z}\right)}={ze}^{{z}\gamma} \underset{{m}=\mathrm{1}} {\overset{+\infty} {\prod}}\:\left(\mathrm{1}+\frac{{z}}{{m}}\right){e}^{−\frac{{z}}{{m}}} \\ $$$$\gamma\:\mathrm{is}\:\mathrm{euler}\:\mathrm{macheroni}\:\mathrm{constant}\:\left(\mathrm{Q2818},\mathrm{Q2783}\right) \\ $$

Commented by Filup last updated on 30/Nov/15

z(z+1)(z+2)∙∙∙(z+n)=(((z+n)!)/((z−1)!)) ∴Γ(z)=lim_(n→+∞) ((n!∙(z−1)!)/((z+n)!))∙n^z

$${z}\left({z}+\mathrm{1}\right)\left({z}+\mathrm{2}\right)\centerdot\centerdot\centerdot\left({z}+{n}\right)=\frac{\left({z}+{n}\right)!}{\left({z}−\mathrm{1}\right)!} \\ $$$$\therefore\Gamma\left({z}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{n}!\centerdot\left({z}−\mathrm{1}\right)!}{\left({z}+{n}\right)!}\centerdot{n}^{{z}} \\ $$

Answered by Filup last updated on 30/Nov/15

Γ(z)=(z−1)(z−2)∙∙∙×3×2×1 Γ(z+1)=z(z−1)(z−2)∙∙∙×3×2×1 Γ(z+1)=zΓ(z) I′m sure you wanted a proof in terms of the limit you gave above, but I am unsure as to how to achieve the result you most likely desired. Maybe you can further prove by applying the limit? I shall update this post if I can. I might have an idea to prove (i) in terms of the limit

$$\Gamma\left({z}\right)=\left({z}−\mathrm{1}\right)\left({z}−\mathrm{2}\right)\centerdot\centerdot\centerdot×\mathrm{3}×\mathrm{2}×\mathrm{1} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)={z}\left({z}−\mathrm{1}\right)\left({z}−\mathrm{2}\right)\centerdot\centerdot\centerdot×\mathrm{3}×\mathrm{2}×\mathrm{1} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right) \\ $$$$ \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{sure}\:\mathrm{you}\:\mathrm{wanted}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{limit}\:\mathrm{you}\:\mathrm{gave}\:\mathrm{above},\:\mathrm{but}\:\mathrm{I}\:\mathrm{am} \\ $$$$\mathrm{unsure}\:\mathrm{as}\:\mathrm{to}\:\mathrm{how}\:\mathrm{to}\:\mathrm{achieve}\:\mathrm{the}\:\mathrm{result} \\ $$$$\mathrm{you}\:\mathrm{most}\:\mathrm{likely}\:\mathrm{desired}.\:\mathrm{Maybe}\:\mathrm{you}\:\mathrm{can} \\ $$$$\mathrm{further}\:\mathrm{prove}\:\mathrm{by}\:\mathrm{applying}\:\mathrm{the}\:\mathrm{limit}? \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{shall}\:\mathrm{update}\:\mathrm{this}\:\mathrm{post}\:\mathrm{if}\:\mathrm{I}\:\mathrm{can}.\:\mathrm{I}\:{might} \\ $$$$\mathrm{have}\:\mathrm{an}\:\mathrm{idea}\:\mathrm{to}\:\mathrm{prove}\:\left({i}\right)\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{limit} \\ $$

Commented by 123456 last updated on 30/Nov/15

the limit above is the most general definition possible for Γ (analitic continuation of Γ) its extend Γ to almost all C(with exeption of negatives number and 0) however its is so hard to use

$$\mathrm{the}\:\mathrm{limit}\:\mathrm{above}\:\mathrm{is}\:\mathrm{the}\:\mathrm{most}\:\mathrm{general}\:\mathrm{definition} \\ $$$$\mathrm{possible}\:\mathrm{for}\:\Gamma\:\left(\mathrm{analitic}\:\mathrm{continuation}\:\mathrm{of}\:\Gamma\right) \\ $$$$\mathrm{its}\:\mathrm{extend}\:\Gamma\:\mathrm{to}\:\mathrm{almost}\:\mathrm{all}\:\mathbb{C}\left(\mathrm{with}\:\mathrm{exeption}\right. \\ $$$$\left.\mathrm{of}\:\mathrm{negatives}\:\mathrm{number}\:\mathrm{and}\:\mathrm{0}\right) \\ $$$$\mathrm{however}\:\mathrm{its}\:\mathrm{is}\:\mathrm{so}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{use} \\ $$

Commented by Filup last updated on 30/Nov/15

I am trying a method of proof now. If it leads nowhere, i′ll delete my 2nd post

$$\mathrm{I}\:\mathrm{am}\:\mathrm{trying}\:\mathrm{a}\:\mathrm{method}\:\mathrm{of}\:\mathrm{proof}\:\mathrm{now}. \\ $$$$\mathrm{If}\:\mathrm{it}\:\mathrm{leads}\:\mathrm{nowhere},\:\mathrm{i}'\mathrm{ll}\:\mathrm{delete}\:\mathrm{my}\:\mathrm{2nd}\:\mathrm{post} \\ $$

Answered by Filup last updated on 30/Nov/15

Proof with limit Γ(z)=lim_(n→∞) ((n!)/(z(z+1)∙∙∙(z+n)))n^z ∴Γ(z)=lim_(n→∞) ((n!(z−1)!)/((z+n)!))n^z Show that Γ(z)=(z−1)Γ(z−1) ∴lim_(n→∞) ((n!(z−1)!)/((z+n)!))n^z =(z−1)(lim_(n→∞) ((n!(z−2)!)/((z+n−1)!))n^(z−1) ) Let us assume Γ(z)=(z−1)Γ(z−1). If this is true then LHS=RHS Γ(x)=(x−1)! lim_(n→∞) ((n!∙Γ(z))/(Γ(z+n+1)))n^z =(z−1)(lim_(n→∞) ((n!∙Γ(z−1))/(Γ(z+n)))n^(z−1) ) ∴lim_(n→∞) ((n!∙Γ(z))/(Γ(z+n+1)))n^z =(z−1)(lim_(n→∞) ((n!∙((Γ(z))/(z−1)))/((Γ(z+n+1))/(z−1)))n^(z−1) ) ∴lim_(n→∞) ((n!∙Γ(z))/(Γ(z+n+1)))n^z =(z−1)(lim_(n→∞) (((n!∙Γ(z)∙(z−1))/((z−1)∙Γ(z+n+1))))n^(z−1) ) ∴lim_(n→∞) ((n!∙Γ(z))/(Γ(z+n+1)))n^z =lim_(n→∞) (((z−1)∙n!∙Γ(z))/(Γ(z+n+1)))n^(z−1) Γ(z+n+1)=(z+n)! ∴lim_(n→∞) ((n!∙Γ(z))/((z+n)!))n^z =lim_(n→∞) ((n!∙Γ(z)^2 )/((z+n)!∙Γ(z−1)))n^(z−1) ∴lim_(n→∞) ((n!)/((z+n)!))n^z =lim_(n→∞) ((n!∙Γ(z))/((z+n)!∙Γ(z−1)))n^(z−1) ∴lim_(n→∞) ((n!)/((z+n)!))n^z =lim_(n→∞) ((n!∙(z−1))/((z+n)!))n^(z−1) lim_(x→∞) ((x!)/((x+a)!))=1 (?) ∴lim_(n→∞) n^z =lim_(n→∞) (z−1)n^(z−1) TRUE ∴Γ(z+1)=zΓ(z) please let me know of any errors

$${Proof}\:{with}\:{limit} \\ $$$$\Gamma\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!}{{z}\left({z}+\mathrm{1}\right)\centerdot\centerdot\centerdot\left({z}+{n}\right)}{n}^{{z}} \\ $$$$\therefore\Gamma\left({z}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\left({z}−\mathrm{1}\right)!}{\left({z}+{n}\right)!}{n}^{{z}} \\ $$$$ \\ $$$$\mathrm{Show}\:\mathrm{that}\:\Gamma\left({z}\right)=\left({z}−\mathrm{1}\right)\Gamma\left({z}−\mathrm{1}\right) \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\left({z}−\mathrm{1}\right)!}{\left({z}+{n}\right)!}{n}^{{z}} =\left({z}−\mathrm{1}\right)\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\left({z}−\mathrm{2}\right)!}{\left({z}+{n}−\mathrm{1}\right)!}{n}^{{z}−\mathrm{1}} \right) \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{assume}\:\Gamma\left({z}\right)=\left({z}−\mathrm{1}\right)\Gamma\left({z}−\mathrm{1}\right).\:\mathrm{If}\:\mathrm{this}\:\mathrm{is} \\ $$$$\mathrm{true}\:\mathrm{then}\:\mathrm{LHS}=\mathrm{RHS} \\ $$$$ \\ $$$$\Gamma\left({x}\right)=\left({x}−\mathrm{1}\right)! \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)}{\Gamma\left({z}+{n}+\mathrm{1}\right)}{n}^{{z}} =\left({z}−\mathrm{1}\right)\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}−\mathrm{1}\right)}{\Gamma\left({z}+{n}\right)}{n}^{{z}−\mathrm{1}} \right) \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)}{\Gamma\left({z}+{n}+\mathrm{1}\right)}{n}^{{z}} =\left({z}−\mathrm{1}\right)\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\frac{\Gamma\left({z}\right)}{{z}−\mathrm{1}}}{\frac{\Gamma\left({z}+{n}+\mathrm{1}\right)}{{z}−\mathrm{1}}}{n}^{{z}−\mathrm{1}} \right) \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)}{\Gamma\left({z}+{n}+\mathrm{1}\right)}{n}^{{z}} =\left({z}−\mathrm{1}\right)\left(\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{n}!\centerdot\Gamma\left({z}\right)\centerdot\left({z}−\mathrm{1}\right)}{\left({z}−\mathrm{1}\right)\centerdot\Gamma\left({z}+{n}+\mathrm{1}\right)}\right){n}^{{z}−\mathrm{1}} \right) \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)}{\Gamma\left({z}+{n}+\mathrm{1}\right)}{n}^{{z}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left({z}−\mathrm{1}\right)\centerdot{n}!\centerdot\Gamma\left({z}\right)}{\Gamma\left({z}+{n}+\mathrm{1}\right)}{n}^{{z}−\mathrm{1}} \\ $$$$\Gamma\left({z}+{n}+\mathrm{1}\right)=\left({z}+{n}\right)! \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)}{\left({z}+{n}\right)!}{n}^{{z}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)^{\mathrm{2}} }{\left({z}+{n}\right)!\centerdot\Gamma\left({z}−\mathrm{1}\right)}{n}^{{z}−\mathrm{1}} \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!}{\left({z}+{n}\right)!}{n}^{{z}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\Gamma\left({z}\right)}{\left({z}+{n}\right)!\centerdot\Gamma\left({z}−\mathrm{1}\right)}{n}^{{z}−\mathrm{1}} \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!}{\left({z}+{n}\right)!}{n}^{{z}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!\centerdot\left({z}−\mathrm{1}\right)}{\left({z}+{n}\right)!}{n}^{{z}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}!}{\left({x}+{a}\right)!}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\left(?\right) \\ $$$$\therefore\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{{z}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left({z}−\mathrm{1}\right){n}^{{z}−\mathrm{1}} \\ $$$$\mathrm{TRUE} \\ $$$$\therefore\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right) \\ $$$$\mathrm{please}\:\mathrm{let}\:\mathrm{me}\:\mathrm{know}\:\mathrm{of}\:\mathrm{any}\:\mathrm{errors} \\ $$

Commented by 123456 last updated on 30/Nov/15

Γ(z+1)=zΓ(z) Γ(z)=(z−1)Γ(z−1)

$$\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right) \\ $$$$\Gamma\left({z}\right)=\left({z}−\mathrm{1}\right)\Gamma\left({z}−\mathrm{1}\right) \\ $$

Commented by Filup last updated on 30/Nov/15

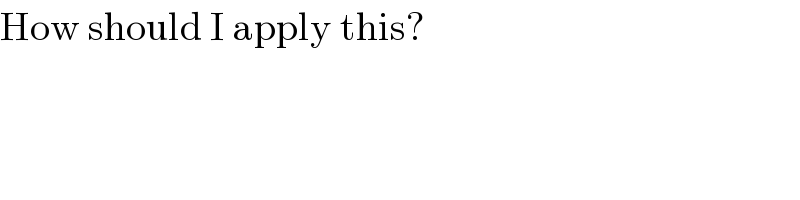
How should I apply this?

$$\mathrm{How}\:\mathrm{should}\:\mathrm{I}\:\mathrm{apply}\:\mathrm{this}? \\ $$

Commented by 123456 last updated on 30/Nov/15

you have a typo in the 5th line

$$\mathrm{you}\:\mathrm{have}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{in}\:\mathrm{the}\:\mathrm{5th}\:\mathrm{line} \\ $$

Commented by Filup last updated on 30/Nov/15

Thanks! I′ll re read everything! I believe I have fixed everything

$$\mathrm{T}{hanks}!\:{I}'{ll}\:{re}\:{read}\:{everything}! \\ $$$$\mathrm{I}\:\mathrm{believe}\:\mathrm{I}\:\mathrm{have}\:\mathrm{fixed}\:\mathrm{everything} \\ $$

Commented by 123456 last updated on 30/Nov/15

hint: (x/x)=1,lim_(n→∞) ((n+a)/(n+b))=1 try to write Γ(z) and Γ(z+1) and compare each other to see what you need to manipulate :D ps:if you want i can post the proof for this part, but try to do it

$$\mathrm{hint}:\:\frac{{x}}{{x}}=\mathrm{1},\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}+{a}}{{n}+{b}}=\mathrm{1} \\ $$$$\mathrm{try}\:\mathrm{to}\:\mathrm{write}\:\Gamma\left({z}\right)\:\mathrm{and}\:\Gamma\left({z}+\mathrm{1}\right) \\ $$$$\mathrm{and}\:\mathrm{compare}\:\mathrm{each}\:\mathrm{other}\:\mathrm{to}\:\mathrm{see}\:\mathrm{what} \\ $$$$\mathrm{you}\:\mathrm{need}\:\mathrm{to}\:\mathrm{manipulate}\::\mathrm{D} \\ $$$$\mathrm{ps}:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{i}\:\mathrm{can}\:\mathrm{post}\:\mathrm{the}\:\mathrm{proof}\:\mathrm{for}\:\mathrm{this} \\ $$$$\mathrm{part},\:\mathrm{but}\:\mathrm{try}\:\mathrm{to}\:\mathrm{do}\:\mathrm{it} \\ $$

Commented by Filup last updated on 30/Nov/15

I′ll let you know if i can′t do it!

$$\mathrm{I}'\mathrm{ll}\:\mathrm{let}\:\mathrm{you}\:\mathrm{know}\:\mathrm{if}\:\mathrm{i}\:\mathrm{can}'\mathrm{t}\:\mathrm{do}\:\mathrm{it}! \\ $$

Commented by Filup last updated on 30/Nov/15

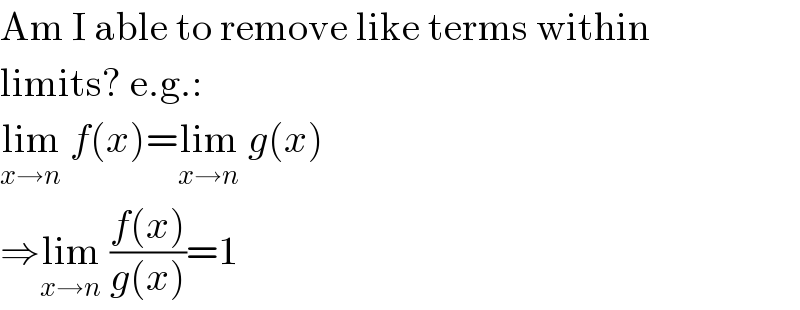
Am I able to remove like terms within limits? e.g.: lim_(x→n) f(x)=lim_(x→n) g(x) ⇒lim_(x→n) ((f(x))/(g(x)))=1

$$\mathrm{Am}\:\mathrm{I}\:\mathrm{able}\:\mathrm{to}\:\mathrm{remove}\:\mathrm{like}\:\mathrm{terms}\:\mathrm{within} \\ $$$$\mathrm{limits}?\:\mathrm{e}.\mathrm{g}.: \\ $$$$\underset{{x}\rightarrow{n}} {\mathrm{lim}}\:{f}\left({x}\right)=\underset{{x}\rightarrow{n}} {\mathrm{lim}}\:{g}\left({x}\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow{n}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\mathrm{1} \\ $$

Commented by Filup last updated on 30/Nov/15

is this correct?

$$\mathrm{is}\:\mathrm{this}\:\mathrm{correct}? \\ $$

Answered by Yozzi last updated on 30/Nov/15

(i) We are given Γ(z)=lim_(n→+∞) ((n!n^z )/(Π_(r=0) ^n (z+r))). Here I assume z is such that the function Γ(z) is well defined. A possible constriction on the domain for Γ is z>0. Therefore we have Γ(z+1)=lim_(n→+∞) ((n!n^(z+1) )/((z+1)(z+2)...(z+n)(z+n+1))) Γ(z+1)=lim_(n→+∞) ((n!n^(z+1) z)/({Π_(r=0) ^n (z+r)}(z+1+n))) Γ(z+1)=lim_(n→+∞) (((n!n^z )/(Π_(r=0) ^n (z+r))))×((zn)/(z+1+n)) Since lim_(x→+∞) f(x)×g(x)=(lim_(x→+∞) f(x))(lim_(x→+∞) g(x)) in general, we obtain Γ(z+1)=Γ(z)×lim_(n→+∞) ((zn)/(z+1+n)). But, ((zn)/(z+1+n))=(z/((z/n)+(1/n)+1)). ⇒Γ(z+1)=Γ(z)lim_(n→+∞) (z/((z/n)+(1/n)+1)) Γ(z+1)=Γ(z)×(z/((z/∞)+(1/∞)+1)) Γ(z+1)=Γ(z)×(z/(0+0+1)) Γ(z+1)=zΓ(z). □ Remarks: (1) If it is required to calculate the value of Γ(x) for x<0 we use the recurrence relation Γ(x)=(1/x)Γ(x+1) until the part Γ(x+1) reduces fully to some non−negative form. E.g Γ(((−5)/2))=((−2)/5)Γ(((−3)/2))=((−2)/5)×((−2)/3)Γ(((−1)/2)) Γ(−(5/2))=(4/(15))×((−2)/1)Γ((1/2)) Since Γ(1/2)=(√π), Γ(((−5)/2))=((−8)/(15))(√π). (2) For 0<x<1 we have Γ(x)Γ(1−x)=(π/(sinπz)). So, if x=1/2 we derive the result Γ(0.5)=(√π). Γ(0.5)Γ(1−0.5)=(π/(sin0.5π)) (Γ(0.5))^2 =(π/1)⇒Γ(0.5)=±(√π) However, for x>0 the limit definition for Γ(x)=lim_(n→+∞) ((n!n^x )/(Π_(r=0) ^n (x+r))) indicates that Γ(x) is non−negative. ⇒Γ(0.5)≠−(√π)⇒Γ(0.5)=(√π) .

$$\left({i}\right)\:{We}\:{are}\:{given} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Gamma\left({z}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{n}!{n}^{{z}} }{\underset{{r}=\mathrm{0}} {\overset{{n}} {\prod}}\left({z}+{r}\right)}.\: \\ $$$${Here}\:{I}\:{assume}\:{z}\:{is}\:{such}\:{that}\:{the}\: \\ $$$${function}\:\Gamma\left({z}\right)\:{is}\:{well}\:{defined}.\:{A}\: \\ $$$${possible}\:{constriction}\:{on}\:{the}\:{domain} \\ $$$${for}\:\Gamma\:{is}\:{z}>\mathrm{0}.\:{Therefore}\:{we}\:{have} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{n}!{n}^{{z}+\mathrm{1}} }{\left({z}+\mathrm{1}\right)\left({z}+\mathrm{2}\right)...\left({z}+{n}\right)\left({z}+{n}+\mathrm{1}\right)} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{n}!{n}^{{z}+\mathrm{1}} {z}}{\left\{\underset{{r}=\mathrm{0}} {\overset{{n}} {\prod}}\left({z}+{r}\right)\right\}\left({z}+\mathrm{1}+{n}\right)} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{n}!{n}^{{z}} }{\underset{{r}=\mathrm{0}} {\overset{{n}} {\prod}}\left({z}+{r}\right)}\right)×\frac{{zn}}{{z}+\mathrm{1}+{n}} \\ $$$${Since}\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)×{g}\left({x}\right)=\left(\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)\right)\left(\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{g}\left({x}\right)\right)\:{in} \\ $$$${general},\:{we}\:{obtain} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)=\Gamma\left({z}\right)×\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{zn}}{{z}+\mathrm{1}+{n}}. \\ $$$${But},\:\frac{{zn}}{{z}+\mathrm{1}+{n}}=\frac{{z}}{\frac{{z}}{{n}}+\frac{\mathrm{1}}{{n}}+\mathrm{1}}. \\ $$$$\Rightarrow\Gamma\left({z}+\mathrm{1}\right)=\Gamma\left({z}\right)\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{z}}{\frac{{z}}{{n}}+\frac{\mathrm{1}}{{n}}+\mathrm{1}} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)=\Gamma\left({z}\right)×\frac{{z}}{\frac{{z}}{\infty}+\frac{\mathrm{1}}{\infty}+\mathrm{1}} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)=\Gamma\left({z}\right)×\frac{{z}}{\mathrm{0}+\mathrm{0}+\mathrm{1}} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right).\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$$ \\ $$$${Remarks}: \\ $$$$\left(\mathrm{1}\right)\:{If}\:{it}\:{is}\:{required}\:{to}\:{calculate}\:{the}\: \\ $$$${value}\:{of}\:\Gamma\left({x}\right)\:{for}\:{x}<\mathrm{0}\:{we}\:{use}\:{the} \\ $$$${recurrence}\:{relation}\:\Gamma\left({x}\right)=\frac{\mathrm{1}}{{x}}\Gamma\left({x}+\mathrm{1}\right) \\ $$$${until}\:{the}\:{part}\:\Gamma\left({x}+\mathrm{1}\right)\:{reduces}\:{fully}\:{to}\: \\ $$$${some}\:{non}−{negative}\:{form}. \\ $$$${E}.{g}\:\:\Gamma\left(\frac{−\mathrm{5}}{\mathrm{2}}\right)=\frac{−\mathrm{2}}{\mathrm{5}}\Gamma\left(\frac{−\mathrm{3}}{\mathrm{2}}\right)=\frac{−\mathrm{2}}{\mathrm{5}}×\frac{−\mathrm{2}}{\mathrm{3}}\Gamma\left(\frac{−\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(−\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{4}}{\mathrm{15}}×\frac{−\mathrm{2}}{\mathrm{1}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${Since}\:\Gamma\left(\mathrm{1}/\mathrm{2}\right)=\sqrt{\pi}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Gamma\left(\frac{−\mathrm{5}}{\mathrm{2}}\right)=\frac{−\mathrm{8}}{\mathrm{15}}\sqrt{\pi}. \\ $$$$\left(\mathrm{2}\right)\:{For}\:\mathrm{0}<{x}<\mathrm{1}\:{we}\:{have}\: \\ $$$$\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)=\frac{\pi}{{sin}\pi{z}}. \\ $$$${So},\:{if}\:{x}=\mathrm{1}/\mathrm{2}\:{we}\:{derive}\:{the}\:{result} \\ $$$$\Gamma\left(\mathrm{0}.\mathrm{5}\right)=\sqrt{\pi}. \\ $$$$\Gamma\left(\mathrm{0}.\mathrm{5}\right)\Gamma\left(\mathrm{1}−\mathrm{0}.\mathrm{5}\right)=\frac{\pi}{{sin}\mathrm{0}.\mathrm{5}\pi} \\ $$$$\left(\Gamma\left(\mathrm{0}.\mathrm{5}\right)\right)^{\mathrm{2}} =\frac{\pi}{\mathrm{1}}\Rightarrow\Gamma\left(\mathrm{0}.\mathrm{5}\right)=\pm\sqrt{\pi} \\ $$$${However},\:{for}\:{x}>\mathrm{0}\:{the}\:{limit}\:{definition} \\ $$$${for}\:\Gamma\left({x}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{n}!{n}^{{x}} }{\underset{{r}=\mathrm{0}} {\overset{{n}} {\prod}}\left({x}+{r}\right)}\:{indicates}\:{that} \\ $$$$\Gamma\left({x}\right)\:{is}\:{non}−{negative}. \\ $$$$\Rightarrow\Gamma\left(\mathrm{0}.\mathrm{5}\right)\neq−\sqrt{\pi}\Rightarrow\Gamma\left(\mathrm{0}.\mathrm{5}\right)=\sqrt{\pi}\:.\:\:\:\: \\ $$$$ \\ $$$$ \\ $$

Commented by 123456 last updated on 02/Dec/15

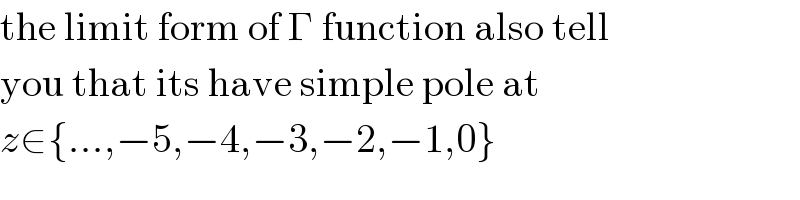
the limit form of Γ function also tell you that its have simple pole at z∈{...,−5,−4,−3,−2,−1,0}

$$\mathrm{the}\:\mathrm{limit}\:\mathrm{form}\:\mathrm{of}\:\Gamma\:\mathrm{function}\:\mathrm{also}\:\mathrm{tell} \\ $$$$\mathrm{you}\:\mathrm{that}\:\mathrm{its}\:\mathrm{have}\:\mathrm{simple}\:\mathrm{pole}\:\mathrm{at} \\ $$$${z}\in\left\{...,−\mathrm{5},−\mathrm{4},−\mathrm{3},−\mathrm{2},−\mathrm{1},\mathrm{0}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com