
Question Number 29000 by abdo imad last updated on 03/Feb/18

$${prove}\:{thst}\:\:\:\:\int_{\mathbb{R}} \:\:\:\:\frac{{e}^{{i}\xi{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\:\pi\:{e}^{−\mid\xi\mid} \:\:. \\ $$
Commented by abdo imad last updated on 04/Feb/18
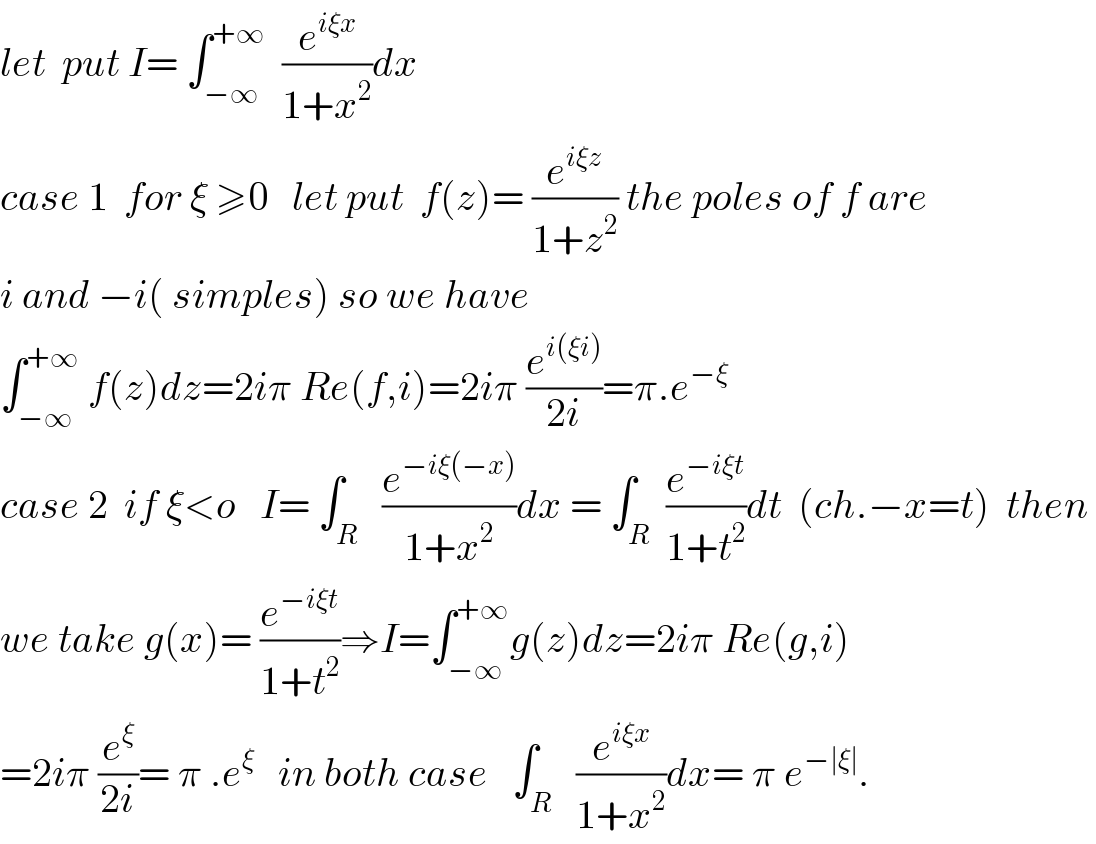
$${let}\:\:{put}\:{I}=\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\xi{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\: \\ $$$${case}\:\mathrm{1}\:\:{for}\:\xi\:\geqslant\mathrm{0}\:\:\:{let}\:{put}\:\:{f}\left({z}\right)=\:\frac{{e}^{{i}\xi{z}} }{\mathrm{1}+{z}^{\mathrm{2}} }\:{the}\:{poles}\:{of}\:{f}\:{are} \\ $$$${i}\:{and}\:−{i}\left(\:{simples}\right)\:{so}\:{we}\:{have}\: \\ $$$$\int_{−\infty} ^{+\infty} \:{f}\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Re}\left({f},{i}\right)=\mathrm{2}{i}\pi\:\frac{{e}^{{i}\left(\xi{i}\right)} }{\mathrm{2}{i}}=\pi.{e}^{−\xi\:} \:\:\: \\ $$$${case}\:\mathrm{2}\:\:{if}\:\xi<{o}\:\:\:{I}=\:\int_{{R}} \:\:\frac{{e}^{−{i}\xi\left(−{x}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\:\int_{{R}} \:\frac{{e}^{−{i}\xi{t}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\left({ch}.−{x}={t}\right)\:\:{then}\: \\ $$$${we}\:{take}\:{g}\left({x}\right)=\:\frac{{e}^{−{i}\xi{t}} }{\mathrm{1}+{t}^{\mathrm{2}} }\Rightarrow{I}=\int_{−\infty} ^{+\infty} {g}\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Re}\left({g},{i}\right) \\ $$$$=\mathrm{2}{i}\pi\:\frac{{e}^{\xi} }{\mathrm{2}{i}}=\:\pi\:.{e}^{\xi} \:\:\:{in}\:{both}\:{case}\:\:\:\int_{{R}} \:\:\frac{{e}^{{i}\xi{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\:\pi\:{e}^{−\mid\xi\mid} . \\ $$
