
Question and Answers Forum
Question Number 29038 by abdo imad last updated on 03/Feb/18
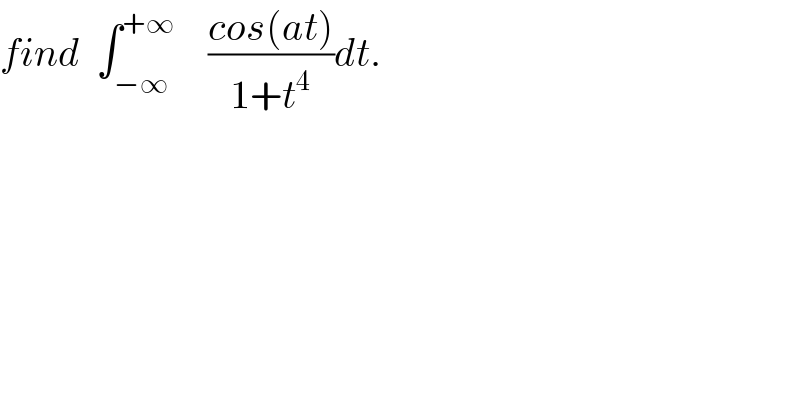
Commented by abdo imad last updated on 11/Feb/18
![let put I(a)= ∫^(+∞) _(−∞) ((cos(at))/(1+t^4 ))dt =Re(∫_(−∞) ^(+∞) (e^(iat) /(1+t^4 ))dt)let introduce the complex functionϕ(z)= (e^(iaz) /(1+z^4 )) poles of ϕ? z^4 =−1 ⇔z^4 =e^(iπ) if z= r e^(iθ) ⇒ r=1 and 4θ =(2k+1)π ⇒θ=(2k+1)(π/4) so the poles of ϕ are z_k =e^(i(2k+1)(π/4)) and k∈[[o,3]] z_0 = e^(i(π/4)) , z_1 =e^(i((3π)/4)) , z_2 =e^(i((5π)/4)) , z_3 =e^(k((7π)/4)) ϕ(z)= (e^(iaz) /((z−z_0 )(z−z_1 )(z−z_2 )(z−z_3 ))) ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ(Re(ϕ,z_0 ) +Re(ϕ,z_1 )) Res(ϕ,z_0 )= (e^(iaz_0 ) /(4z_0^ ^3 )) =−(1/4)z_0 e^(iaz_0 ) Res(ϕ,z_1 )= (e^(iaz_1 ) /(4z_1 ^3 ))=−(1/4)z_1 e^(iaz_1 ) but z_1 =z_0 ^− ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ(−(1/4))( z_0 e^(iaz_0 ) +z_0 ^− e^(iaz_0 ^− ) ) =−((iπ)/2)( z_0 e^(iaz_0 ) +z_0 ^− e^(iaz_9 ^− ) )....be continued....](Q29640.png)
| ||
Question and Answers Forum | ||
Question Number 29038 by abdo imad last updated on 03/Feb/18 | ||
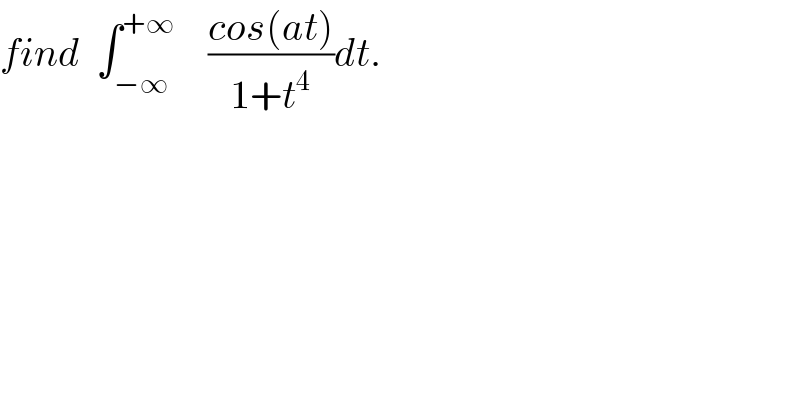 | ||
Commented by abdo imad last updated on 11/Feb/18 | ||
![let put I(a)= ∫^(+∞) _(−∞) ((cos(at))/(1+t^4 ))dt =Re(∫_(−∞) ^(+∞) (e^(iat) /(1+t^4 ))dt)let introduce the complex functionϕ(z)= (e^(iaz) /(1+z^4 )) poles of ϕ? z^4 =−1 ⇔z^4 =e^(iπ) if z= r e^(iθ) ⇒ r=1 and 4θ =(2k+1)π ⇒θ=(2k+1)(π/4) so the poles of ϕ are z_k =e^(i(2k+1)(π/4)) and k∈[[o,3]] z_0 = e^(i(π/4)) , z_1 =e^(i((3π)/4)) , z_2 =e^(i((5π)/4)) , z_3 =e^(k((7π)/4)) ϕ(z)= (e^(iaz) /((z−z_0 )(z−z_1 )(z−z_2 )(z−z_3 ))) ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ(Re(ϕ,z_0 ) +Re(ϕ,z_1 )) Res(ϕ,z_0 )= (e^(iaz_0 ) /(4z_0^ ^3 )) =−(1/4)z_0 e^(iaz_0 ) Res(ϕ,z_1 )= (e^(iaz_1 ) /(4z_1 ^3 ))=−(1/4)z_1 e^(iaz_1 ) but z_1 =z_0 ^− ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ(−(1/4))( z_0 e^(iaz_0 ) +z_0 ^− e^(iaz_0 ^− ) ) =−((iπ)/2)( z_0 e^(iaz_0 ) +z_0 ^− e^(iaz_9 ^− ) )....be continued....](Q29640.png) | ||