
Question and Answers Forum
Question Number 29134 by Tinkutara last updated on 04/Feb/18

Commented by ajfour last updated on 04/Feb/18
Commented by ajfour last updated on 04/Feb/18
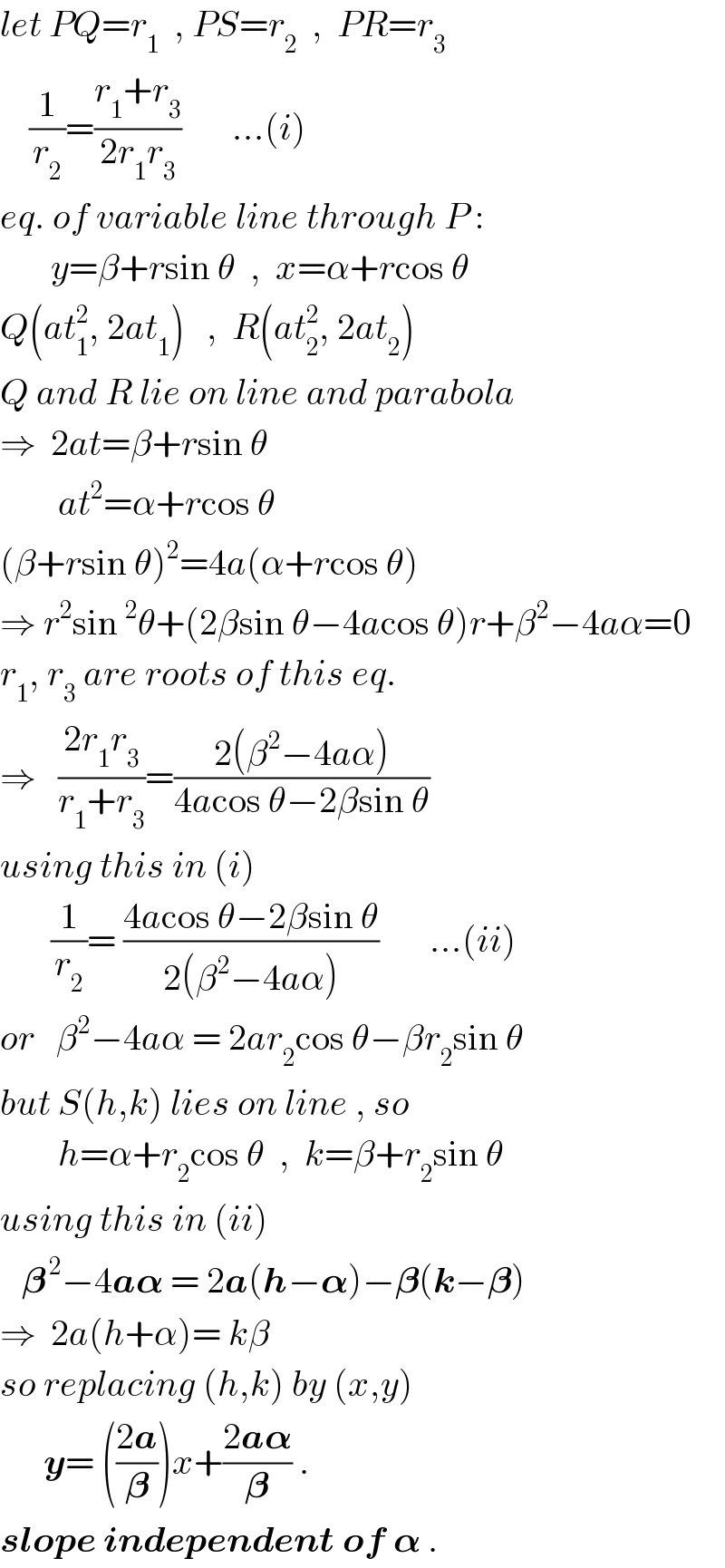
Commented by Tinkutara last updated on 05/Feb/18
Wonderful Sir! ���� Thanks! ��
