Question Number 29209 by tawa tawa last updated on 05/Feb/18
Commented by tawa tawa last updated on 05/Feb/18
$$\mathrm{please}\:\mathrm{help}\:\mathrm{with}.\:\:\mathrm{4},\:\mathrm{5},\:\mathrm{6},\:\mathrm{7} \\ $$
Commented by ajfour last updated on 05/Feb/18
Commented by ajfour last updated on 05/Feb/18
$$\left.{Q}.\mathrm{4}\right) \\ $$$$\:{let}\:{charge}\:{at}\:{time}\:{t}\:{be}\:{Q}. \\ $$$${And}\:{the}\:{initial}\:{charge}\:{Q}_{\mathrm{0}} . \\ $$$${Kirchoff}'{s}\:{voltage}\:{law}\:{gives} \\ $$$$\:\:\:\frac{{Q}}{{C}}−{iR}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\frac{{Q}}{{RC}}\:=\:−{i}\:=\:\frac{{dQ}}{{dt}} \\ $$$$\Rightarrow\:\:\:\:\int_{{Q}_{\mathrm{0}} } ^{\:\:{Q}} \:\frac{{dQ}}{{Q}}\:=\:−\int_{\mathrm{0}} ^{\:\:{t}} \frac{{dt}}{{RC}} \\ $$$${or}\:\:\:\mathrm{ln}\:\frac{{Q}}{{Q}_{\mathrm{0}} }\:=\:−\frac{{t}}{{RC}} \\ $$$$\Rightarrow\:\:\:{Q}=\:{Q}_{\mathrm{0}} {e}^{−\frac{{t}}{{RC}}} \:\:\:\:. \\ $$$$ \\ $$$$\left.{Q}.\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{v}_{\mathrm{0}} =\:\frac{{Q}_{\mathrm{0}} }{{C}}\:\:\:,\:\:\:{v}\:=\:\frac{{Q}}{{C}} \\ $$$${So}\:\:\:\:\:{from}\:{result}\:{of}\:{Q}.\left(\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:{v}\:=\:{v}_{\mathrm{0}} {e}^{−\frac{{t}}{{RC}}} \:\:\:. \\ $$
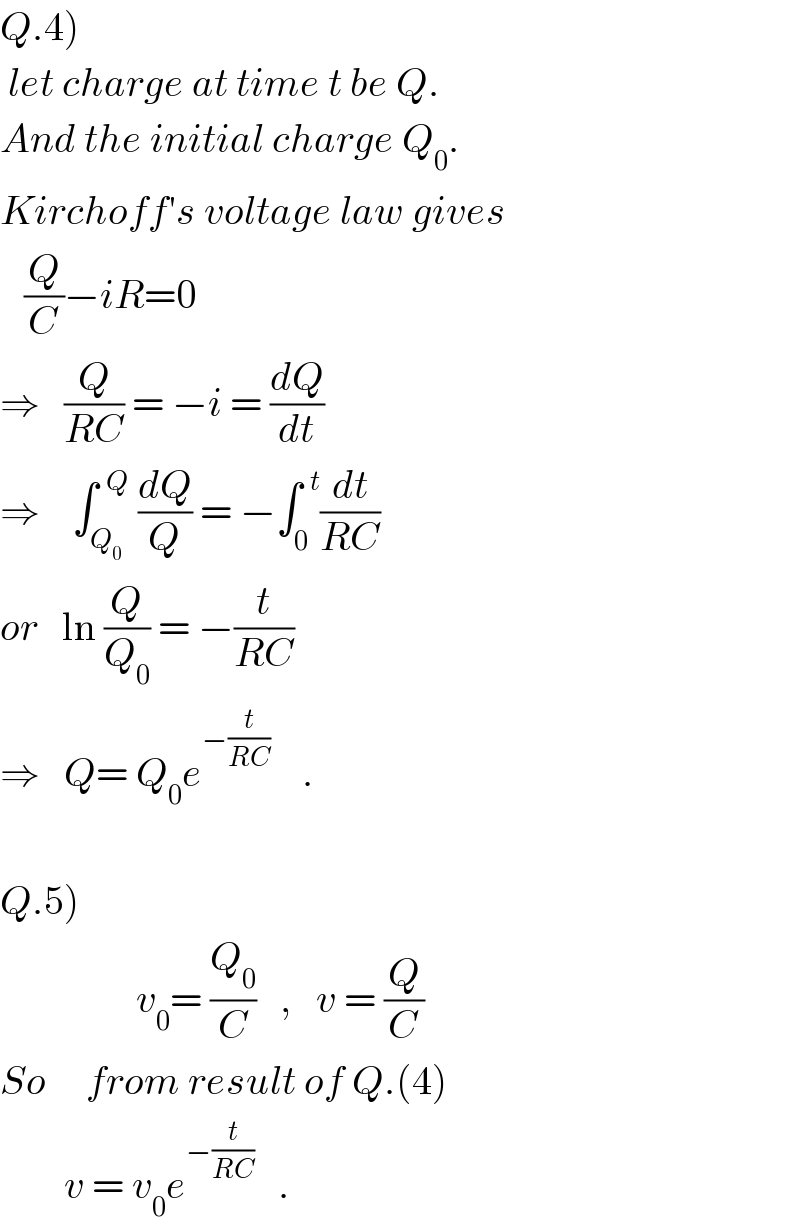
Commented by tawa tawa last updated on 05/Feb/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate} \\ $$
Answered by ajfour last updated on 05/Feb/18
![Q.6) ((Ldi)/dt)+iR = Ecos ωt ⇒ (di/dt) +((iR)/L) = (E/L)cos ωt integrating factor for the linear differential equation is e^(∫(R/L)dt) =e^(Rt/L) so i(e^(Rt/L) )=(E/L)∫e^(Rt/L) cos ωt =(E/L)[(((sin ωt)/ω))e^(Rt/L) −(R/(ωL))∫e^(Rt/L) sin ωtdt ]+c =(E/L){((e^(Rt/L) sin ωt)/ω)−(R/(ωL))[−((e^(Rt/L) cos ωt)/ω)+(R/(ωL))∫e^(Rt/L) cos ωtdt ]}+c_1 =(E/L){((e^(Rt/L) sin ωt)/ω)−(R/(ωL))[−((e^(Rt/L) cos ωt)/ω)+(R/(ωL))×(L/E)(ie^(Rt/L) )]}+c_1 ⇒ i(e^(Rt/L) )[1+(R^2 /(ω^2 L^2 ))]=(E/(ωL))(e^(Rt/L) )[sin ωt+(R/(ωL))cos ωt]+c_1 ⇒ i = (E/(𝛚^2 L^2 +R^2 ))(𝛚Lsin 𝛚t+Rcos 𝛚t)+c_2 e^(−Rt/L) if i=0 at t=0 0=((ER)/(ω^2 L^2 +R^2 ))+c_2 ⇒ i=(E/(ω^2 L^2 +R^2 ))(ωLsin ωt+Rcos ωt−Re^(−Rt/L) ) .](Q29223.png)
$$\left.{Q}.\mathrm{6}\right)\:\:\:\:\frac{{Ldi}}{{dt}}+{iR}\:=\:{E}\mathrm{cos}\:\omega{t} \\ $$$$\Rightarrow\:\:\:\:\:\frac{{di}}{{dt}}\:+\frac{{iR}}{{L}}\:=\:\frac{{E}}{{L}}\mathrm{cos}\:\omega{t} \\ $$$${integrating}\:{factor}\:{for}\:{the}\:{linear} \\ $$$${differential}\:{equation}\:{is} \\ $$$$\:\:\:\:\:{e}^{\int\frac{{R}}{{L}}{dt}} \:={e}^{{Rt}/{L}} \\ $$$${so}\:\:\:\:\:{i}\left({e}^{{Rt}/{L}} \right)=\frac{{E}}{{L}}\int{e}^{{Rt}/{L}} \mathrm{cos}\:\omega{t} \\ $$$$=\frac{{E}}{{L}}\left[\left(\frac{\mathrm{sin}\:\omega{t}}{\omega}\right){e}^{{Rt}/{L}} −\frac{{R}}{\omega{L}}\int{e}^{{Rt}/{L}} \mathrm{sin}\:\omega{tdt}\:\right]+{c} \\ $$$$=\frac{{E}}{{L}}\left\{\frac{{e}^{{Rt}/{L}} \mathrm{sin}\:\omega{t}}{\omega}−\frac{{R}}{\omega{L}}\left[−\frac{{e}^{{Rt}/{L}} \mathrm{cos}\:\omega{t}}{\omega}+\frac{{R}}{\omega{L}}\int{e}^{{Rt}/{L}} \mathrm{cos}\:\omega{tdt}\:\right]\right\}+{c}_{\mathrm{1}} \\ $$$$=\frac{{E}}{{L}}\left\{\frac{{e}^{{Rt}/{L}} \mathrm{sin}\:\omega{t}}{\omega}−\frac{{R}}{\omega{L}}\left[−\frac{{e}^{{Rt}/{L}} \mathrm{cos}\:\omega{t}}{\omega}+\frac{{R}}{\omega{L}}×\frac{{L}}{{E}}\left({ie}^{{Rt}/{L}} \right)\right]\right\}+{c}_{\mathrm{1}} \\ $$$$\Rightarrow\:{i}\left({e}^{{Rt}/{L}} \right)\left[\mathrm{1}+\frac{{R}^{\mathrm{2}} }{\omega^{\mathrm{2}} {L}^{\mathrm{2}} }\right]=\frac{{E}}{\omega{L}}\left({e}^{{Rt}/{L}} \right)\left[\mathrm{sin}\:\omega{t}+\frac{{R}}{\omega{L}}\mathrm{cos}\:\omega{t}\right]+{c}_{\mathrm{1}} \\ $$$$\Rightarrow\:\boldsymbol{{i}}\:=\:\frac{\boldsymbol{{E}}}{\boldsymbol{\omega}^{\mathrm{2}} \boldsymbol{{L}}^{\mathrm{2}} +\boldsymbol{{R}}^{\mathrm{2}} }\left(\boldsymbol{\omega{L}}\mathrm{sin}\:\boldsymbol{\omega{t}}+\boldsymbol{{R}}\mathrm{cos}\:\boldsymbol{\omega{t}}\right)+\boldsymbol{{c}}_{\mathrm{2}} \boldsymbol{{e}}^{−\boldsymbol{{R}}{t}/\boldsymbol{{L}}} \\ $$$${if}\:\boldsymbol{{i}}=\mathrm{0}\:\:{at}\:{t}=\mathrm{0} \\ $$$$\:\:\:\mathrm{0}=\frac{{ER}}{\omega^{\mathrm{2}} {L}^{\mathrm{2}} +{R}^{\mathrm{2}} }+{c}_{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{i}}=\frac{{E}}{\omega^{\mathrm{2}} {L}^{\mathrm{2}} +{R}^{\mathrm{2}} }\left(\omega{L}\mathrm{sin}\:\omega{t}+{R}\mathrm{cos}\:\omega{t}−{Re}^{−{Rt}/{L}} \right)\:. \\ $$
Commented by tawa tawa last updated on 05/Feb/18
$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$