Question Number 29249 by ajfour last updated on 05/Feb/18
Commented by ajfour last updated on 05/Feb/18
$${Find}\:{side}\:{lengths}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:\:{of}\:\bigtriangleup{ABC} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{r}}_{\mathrm{1}} ,\:\boldsymbol{{r}}_{\mathrm{2}} ,\:{and}\:\boldsymbol{{r}}_{\mathrm{3}} . \\ $$$${We}\:{may}\:{call}\:{r}_{\mathrm{1}} \:{as}\:\boldsymbol{{p}},\: \\ $$$${r}_{\mathrm{2}} \:{as}\:\boldsymbol{{q}}\:{and}\:{r}_{\mathrm{3}} \:{as}\:\boldsymbol{{r}}\:{for}\:{the}\:{sake}\:{of} \\ $$$${convinience}. \\ $$
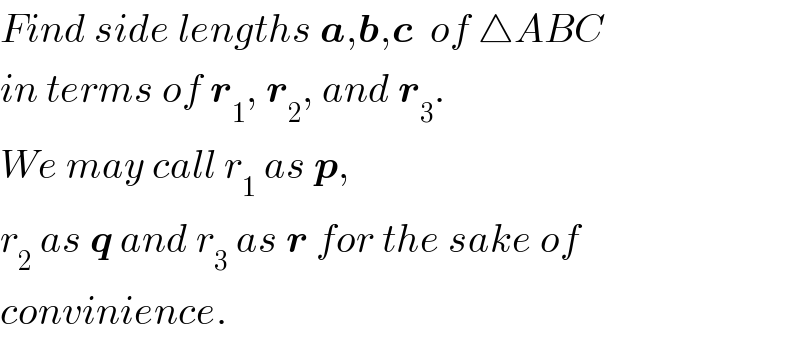
Answered by mrW2 last updated on 05/Feb/18
Commented by mrW2 last updated on 05/Feb/18
![DE=r+p EF=p+q FD=q+r α=sin^(−1) (((p−q)/(p+q))) β=sin^(−1) (((q−r)/(q+r))) γ=sin^(−1) (((r−p)/(r+p))) In ΔDEF we have cos ∠DEF=(((p+q)^2 +(r+p)^2 −(q+r)^2 )/(2(p+q)(r+p))) ⇒cos ∠DEF=((p(p+q)+r(p−q))/((p+q)(r+p))) ⇒u=∠DEF=cos^(−1) [((p(p+q)+r(p−q))/((p+q)(r+p)))] similarly: ⇒cos ∠EFD=((q(q+r)+p(q−r))/((q+r)(p+q))) ⇒v=∠EFD=cos^(−1) [((q(q+r)+p(q−r))/((q+r)(p+q)))] ⇒cos ∠FDE=((r(r+p)+q(r−p))/((r+p)(q+r))) ⇒w=∠FDE=cos^(−1) [((r(r+p)+q(r−p))/((r+p)(q+r)))] ∠B=u−α+γ=cos^(−1) [((p(p+q)+r(p−q))/((p+q)(r+p)))]−sin^(−1) (((p−q)/(p+q)))+sin^(−1) (((r−p)/(r+p))) ∠C=v−β+α=cos^(−1) [((q(q+r)+p(q−r))/((q+r)(p+q)))]−sin^(−1) (((q−r)/(q+r)))+sin^(−1) (((p−q)/(p+q))) ∠A=w−γ+β=cos^(−1) [((r(r+p)+q(r−p))/((r+p)(q+r)))]−sin^(−1) (((r−p)/(r+p)))+sin^(−1) (((q−r)/(q+r))) a=(p/(tan (B/2)))+(√((p+q)^2 −(p−q)^2 ))+(q/(tan (C/2))) ⇒a=((p(1+cos B))/(sin B))+2(√(pq))+((q(1+cos C))/(sin C)) ⇒b=((q(1+cos C))/(sin C))+2(√(qr))+((r(1+cos A))/(sin A)) ⇒c=((r(1+cos A))/(sin A))+2(√(rp))+((p(1+cos B))/(sin B))](Q29252.png)
$${DE}={r}+{p} \\ $$$${EF}={p}+{q} \\ $$$${FD}={q}+{r} \\ $$$$\alpha=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{p}−{q}}{{p}+{q}}\right) \\ $$$$\beta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{q}−{r}}{{q}+{r}}\right) \\ $$$$\gamma=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}−{p}}{{r}+{p}}\right) \\ $$$$ \\ $$$${In}\:\Delta{DEF}\:{we}\:{have} \\ $$$$\mathrm{cos}\:\angle{DEF}=\frac{\left({p}+{q}\right)^{\mathrm{2}} +\left({r}+{p}\right)^{\mathrm{2}} −\left({q}+{r}\right)^{\mathrm{2}} }{\mathrm{2}\left({p}+{q}\right)\left({r}+{p}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:\angle{DEF}=\frac{{p}\left({p}+{q}\right)+{r}\left({p}−{q}\right)}{\left({p}+{q}\right)\left({r}+{p}\right)} \\ $$$$\Rightarrow{u}=\angle{DEF}=\mathrm{cos}^{−\mathrm{1}} \left[\frac{{p}\left({p}+{q}\right)+{r}\left({p}−{q}\right)}{\left({p}+{q}\right)\left({r}+{p}\right)}\right] \\ $$$${similarly}: \\ $$$$\Rightarrow\mathrm{cos}\:\angle{EFD}=\frac{{q}\left({q}+{r}\right)+{p}\left({q}−{r}\right)}{\left({q}+{r}\right)\left({p}+{q}\right)} \\ $$$$\Rightarrow{v}=\angle{EFD}=\mathrm{cos}^{−\mathrm{1}} \left[\frac{{q}\left({q}+{r}\right)+{p}\left({q}−{r}\right)}{\left({q}+{r}\right)\left({p}+{q}\right)}\right] \\ $$$$\Rightarrow\mathrm{cos}\:\angle{FDE}=\frac{{r}\left({r}+{p}\right)+{q}\left({r}−{p}\right)}{\left({r}+{p}\right)\left({q}+{r}\right)} \\ $$$$\Rightarrow{w}=\angle{FDE}=\mathrm{cos}^{−\mathrm{1}} \left[\frac{{r}\left({r}+{p}\right)+{q}\left({r}−{p}\right)}{\left({r}+{p}\right)\left({q}+{r}\right)}\right] \\ $$$$ \\ $$$$\angle{B}={u}−\alpha+\gamma=\mathrm{cos}^{−\mathrm{1}} \left[\frac{{p}\left({p}+{q}\right)+{r}\left({p}−{q}\right)}{\left({p}+{q}\right)\left({r}+{p}\right)}\right]−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{p}−{q}}{{p}+{q}}\right)+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}−{p}}{{r}+{p}}\right) \\ $$$$\angle{C}={v}−\beta+\alpha=\mathrm{cos}^{−\mathrm{1}} \left[\frac{{q}\left({q}+{r}\right)+{p}\left({q}−{r}\right)}{\left({q}+{r}\right)\left({p}+{q}\right)}\right]−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{q}−{r}}{{q}+{r}}\right)+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{p}−{q}}{{p}+{q}}\right) \\ $$$$\angle{A}={w}−\gamma+\beta=\mathrm{cos}^{−\mathrm{1}} \left[\frac{{r}\left({r}+{p}\right)+{q}\left({r}−{p}\right)}{\left({r}+{p}\right)\left({q}+{r}\right)}\right]−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}−{p}}{{r}+{p}}\right)+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{q}−{r}}{{q}+{r}}\right) \\ $$$$ \\ $$$${a}=\frac{{p}}{\mathrm{tan}\:\frac{{B}}{\mathrm{2}}}+\sqrt{\left({p}+{q}\right)^{\mathrm{2}} −\left({p}−{q}\right)^{\mathrm{2}} }+\frac{{q}}{\mathrm{tan}\:\frac{{C}}{\mathrm{2}}} \\ $$$$\Rightarrow{a}=\frac{{p}\left(\mathrm{1}+\mathrm{cos}\:{B}\right)}{\mathrm{sin}\:{B}}+\mathrm{2}\sqrt{{pq}}+\frac{{q}\left(\mathrm{1}+\mathrm{cos}\:{C}\right)}{\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{b}=\frac{{q}\left(\mathrm{1}+\mathrm{cos}\:{C}\right)}{\mathrm{sin}\:{C}}+\mathrm{2}\sqrt{{qr}}+\frac{{r}\left(\mathrm{1}+\mathrm{cos}\:{A}\right)}{\mathrm{sin}\:{A}} \\ $$$$\Rightarrow{c}=\frac{{r}\left(\mathrm{1}+\mathrm{cos}\:{A}\right)}{\mathrm{sin}\:{A}}+\mathrm{2}\sqrt{{rp}}+\frac{{p}\left(\mathrm{1}+\mathrm{cos}\:{B}\right)}{\mathrm{sin}\:{B}} \\ $$
Commented by ajfour last updated on 06/Feb/18
$${Amazing}\:{Sir},\:{thank}\:{you}\:! \\ $$
Commented by mrW2 last updated on 06/Feb/18
