
Question and Answers Forum
Question Number 29320 by Glorious Man last updated on 07/Feb/18
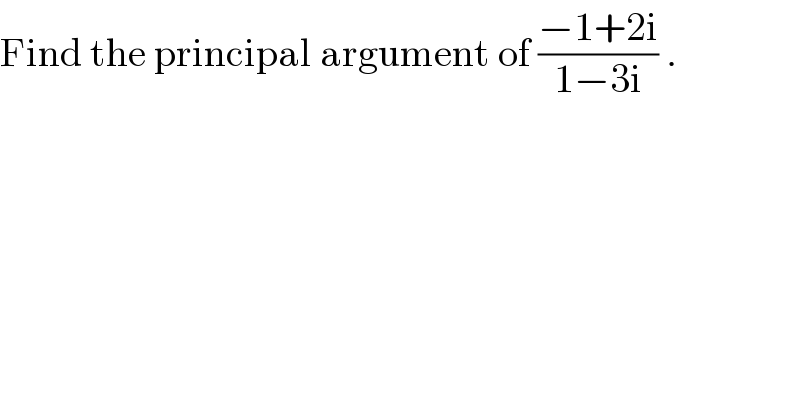
Commented by abdo imad last updated on 08/Feb/18
![∣−1+2i∣=(√5) and −1+2i=(√5)(((−1)/(√5)) +i(2/(√5)))=r e^(iθ) ⇒ r=(√5) and cosθ= ((−1)/(√5)) and sinθ =(2/(√5)) ⇒tanθ =−2 ⇒θ=−actan2 ∣1−3i∣=(√(10)) and 1−3i=(√(10))((1/(√(10))) −(3/(√(10))) i)=r e^(iϕ) ⇒ r=(√(10)) and cosϕ =(1/(√(10))) and sinϕ=−(3/(√(10))) ⇒tanϕ=−3 ⇒ ϕ=−arctan3 so Arg(((−1+2i)/(1−3i)))≡θ −ϕ [2π] ≡ arctan3 −arctan2 [2π] .](Q29357.png)
| ||
Question and Answers Forum | ||
Question Number 29320 by Glorious Man last updated on 07/Feb/18 | ||
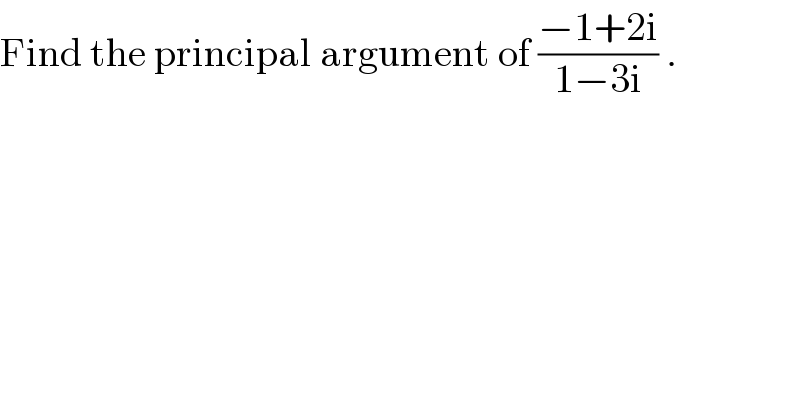 | ||
Commented by abdo imad last updated on 08/Feb/18 | ||
![∣−1+2i∣=(√5) and −1+2i=(√5)(((−1)/(√5)) +i(2/(√5)))=r e^(iθ) ⇒ r=(√5) and cosθ= ((−1)/(√5)) and sinθ =(2/(√5)) ⇒tanθ =−2 ⇒θ=−actan2 ∣1−3i∣=(√(10)) and 1−3i=(√(10))((1/(√(10))) −(3/(√(10))) i)=r e^(iϕ) ⇒ r=(√(10)) and cosϕ =(1/(√(10))) and sinϕ=−(3/(√(10))) ⇒tanϕ=−3 ⇒ ϕ=−arctan3 so Arg(((−1+2i)/(1−3i)))≡θ −ϕ [2π] ≡ arctan3 −arctan2 [2π] .](Q29357.png) | ||