Question and Answers Forum
Question Number 29322 by ajfour last updated on 07/Feb/18
Commented by ajfour last updated on 07/Feb/18
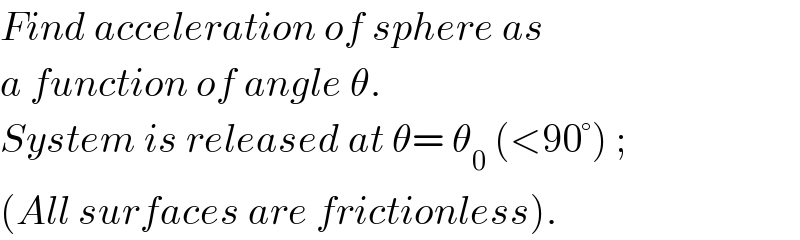
Commented by ajfour last updated on 07/Feb/18

Commented by ajfour last updated on 07/Feb/18
Commented by ajfour last updated on 07/Feb/18
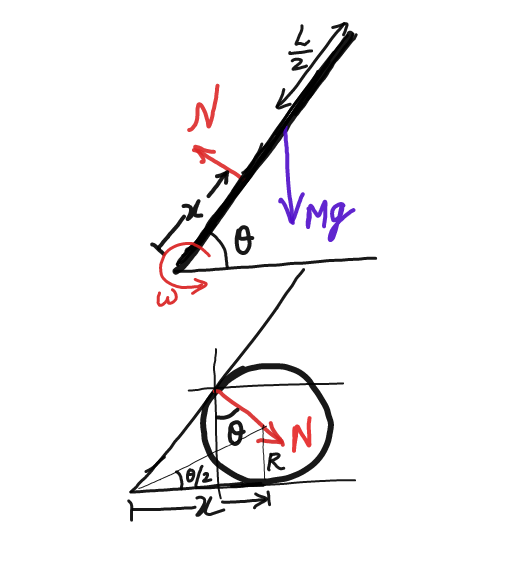
![x=Rcot (θ/2) v=−((ωR)/2)cosec^2 (θ/2) ⇒ v^2 =((𝛚^2 R^2 )/4)cosec^4 (θ/2) ....(i) a=(dv/dt)= −((αR)/2)cosec^2 (θ/2) +((ω^2 R)/2)cosec^2 (θ/2)cot (θ/2) ...(ii) Nsin θ = ma ....(iii) NRcot (θ/2)−((MgLcos θ)/2) =(((ML^2 )/3))α ⇒ α=(3/(ML^2 ))(((maRcot (θ/2))/(sin θ))−((MgLcos θ)/2)) .....(iv) ((MgL)/2)(sin θ_0 −sin θ)=(1/2)mv^2 +(1/2)(((ML^2 )/3))ω^2 using (i): ((MgL)/2)(sin θ_0 −sin θ)=((mω^2 R^2 )/8)cosec^4 (θ/2) +((ML^2 ω^2 )/6) ω^2 =((((MgL)/2)(sin θ_0 −sin θ))/(((ML^2 )/6)+((mR^2 )/8)cosec^4 (θ/2))) ....(A) Using eq. (A), (iii), (iv) in eq.(ii) a=(R/2)cosec^2 (θ/2)((3/(ML^2 )))(((MgLcos θ)/2)−((maRcot (θ/2))/(sin θ))) +(R/2)cosec^2 (θ/2)cot (θ/2)[((((MgL)/2)(sin θ_0 −sin θ))/(((ML^2 )/6)+((mR^2 )/8)cosec^4 (θ/2)))] a[1+((3mR^2 cosec^2 (θ/2)cot (θ/2))/(2ML^2 sin θ))]= (R/2)cosec^2 (θ/2)[((3gcos θ)/(2L))+((((MgL)/2)(sin θ_0 −sin θ)cot (θ/2))/(((ML^2 )/6)+((mR^2 )/8)cosec^4 (θ/2)))] .](Q29333.png)
Commented by mrW2 last updated on 07/Feb/18