Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2936 by Rasheed Soomro last updated on 30/Nov/15

Suppose I want to prove a statement,say P(n), for natural numbers mathematical induction is a proper tool for me. If a P(n) is required to prove for natural n≥c mathematical induction is again a tool of proof. Now suppose I have a statement which is true only for c_1 ≤ n∈N ≤c_2 _(−) . Could I get help for proof from my old friend mathematical induction? If yes how?

$${Suppose}\:{I}\:{want}\:{to}\:{prove}\:{a}\:{statement},{say}\:{P}\left({n}\right),\: \\ $$$${for}\:{natural}\:{numbers}\:\boldsymbol{{mathematical}}\:\boldsymbol{{induction}} \\ $$$${is}\:{a}\:{proper}\:{tool}\:{for}\:{me}. \\ $$$$\mathcal{I}{f}\:{a}\:{P}\left({n}\right)\:{is}\:{required}\:{to}\:{prove}\:{for}\:{natural}\:{n}\geqslant{c}\: \\ $$$${mathematical}\:{induction}\:{is}\:{again}\:{a}\:{tool}\:{of}\:{proof}. \\ $$$$ \\ $$$$\mathcal{N}{ow}\:{suppose}\:{I}\:{have}\:{a}\:{statement}\:{which}\:{is}\:{true} \\ $$$${only}\:{for}\:\:\underset{−} {\:{c}_{\mathrm{1}} \leqslant\:{n}\in\mathbb{N}\:\leqslant{c}_{\mathrm{2}} }\:.\:{Could}\:\mathcal{I}\:{get}\:{help}\:{for}\:{proof}\: \\ $$$${from}\:{my}\:{old}\:{friend}\:\boldsymbol{{mathematical}}\:\boldsymbol{{induction}}? \\ $$$${If}\:{yes}\:{how}? \\ $$$$ \\ $$

Commented by Filup last updated on 01/Dec/15

I belive mathematical induction is used to prove ∀n∈P(n):{n∈N≥c_1 }. I am unsure as to if you can prove within the bounds such that you can show ∀n∈P(n):{c_1 ≤n∈N≤c_2 }. If it was possible, it may be wise to work with and solve for: i) ∀n∉P(n):{n∈N≤c_1 } ii) ∀n∉P(n):{n∈N≥c_2 }

$$\mathrm{I}\:\mathrm{belive}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{is}\:\mathrm{used} \\ $$$$\mathrm{to}\:\mathrm{prove}\:\forall{n}\in{P}\left({n}\right):\left\{{n}\in\mathbb{N}\geqslant{c}_{\mathrm{1}} \right\}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{as}\:\mathrm{to}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{within} \\ $$$$\mathrm{the}\:\mathrm{bounds}\:\mathrm{such}\:\mathrm{that}\:\mathrm{you}\:\mathrm{can}\:\mathrm{show} \\ $$$$\forall{n}\in{P}\left({n}\right):\left\{{c}_{\mathrm{1}} \leqslant{n}\in\mathbb{N}\leqslant{c}_{\mathrm{2}} \right\}. \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{it}\:\mathrm{was}\:\mathrm{possible},\:\mathrm{it}\:\mathrm{may}\:\mathrm{be}\:\mathrm{wise}\:\mathrm{to}\:\mathrm{work} \\ $$$$\mathrm{with}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}: \\ $$$$\left.{i}\right)\:\forall{n}\notin{P}\left({n}\right):\left\{{n}\in\mathbb{N}\leqslant{c}_{\mathrm{1}} \right\} \\ $$$$\left.{ii}\right)\:\forall{n}\notin{P}\left({n}\right):\left\{{n}\in\mathbb{N}\geqslant{c}_{\mathrm{2}} \right\} \\ $$

Commented by Filup last updated on 01/Dec/15

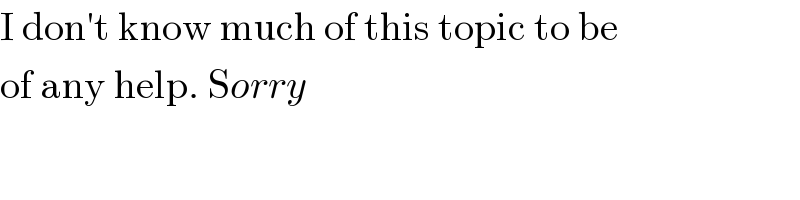
I don′t know much of this topic to be of any help. Sorry

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{much}\:\mathrm{of}\:\mathrm{this}\:\mathrm{topic}\:\mathrm{to}\:\mathrm{be} \\ $$$$\mathrm{of}\:\mathrm{any}\:\mathrm{help}.\:\mathrm{S}{orry} \\ $$

Commented by Rasheed Soomro last updated on 01/Dec/15

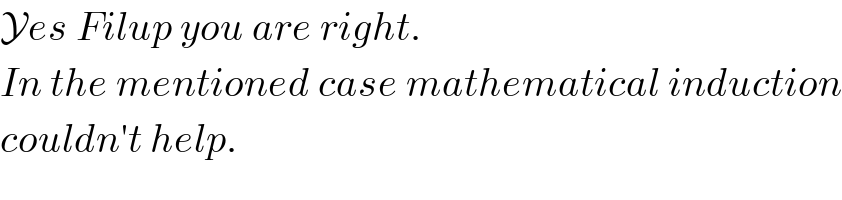
Yes Filup you are right. In the mentioned case mathematical induction couldn′t help.

$$\mathcal{Y}{es}\:{Filup}\:{you}\:{are}\:{right}. \\ $$$${In}\:{the}\:{mentioned}\:{case}\:{mathematical}\:{induction} \\ $$$${couldn}'{t}\:{help}. \\ $$

Commented by 123456 last updated on 02/Dec/15

we can use it to proof things to Z P(n)→P(n+1) P(n)→P(n−1) i think that there some way to use it c_1 ≤n≤c_2 but probraly the bounds will be involved into inductive step

$$\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{it}\:\mathrm{to}\:\mathrm{proof}\:\mathrm{things}\:\mathrm{to}\:\mathbb{Z} \\ $$$$\mathrm{P}\left({n}\right)\rightarrow\mathrm{P}\left({n}+\mathrm{1}\right) \\ $$$$\mathrm{P}\left({n}\right)\rightarrow\mathrm{P}\left({n}−\mathrm{1}\right) \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{that}\:\mathrm{there}\:\mathrm{some}\:\mathrm{way}\:\mathrm{to}\:\mathrm{use}\:\mathrm{it} \\ $$$${c}_{\mathrm{1}} \leqslant{n}\leqslant{c}_{\mathrm{2}} \\ $$$$\mathrm{but}\:\mathrm{probraly}\:\mathrm{the}\:\mathrm{bounds}\:\mathrm{will}\:\mathrm{be}\:\mathrm{involved} \\ $$$$\mathrm{into}\:\mathrm{inductive}\:\mathrm{step} \\ $$

Commented by Rasheed Soomro last updated on 02/Dec/15

Could you clear with an example?

$$\mathcal{C}{ould}\:{you}\:{clear}\:{with}\:{an}\:{example}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com