Question Number 2941 by Syaka last updated on 30/Nov/15
$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{5}}{\mathrm{8}}\:+\:\frac{\mathrm{7}}{\mathrm{16}}\:+\:.......\:=\:\:? \\ $$
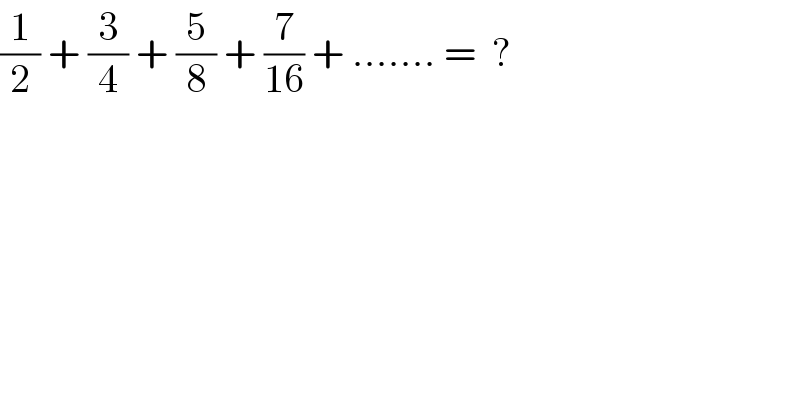
Commented by Syaka last updated on 01/Dec/15
$${Thanks}\:{for}\:{Solution}\:{Sir}\:{Rasheed} \\ $$$${and}\:{also}\:{for}\:{Solved}\:{from}\:{Sir}\:{Yozzi}.\:{Like}\:{that}. \\ $$
Answered by Rasheed Soomro last updated on 01/Dec/15
![Let S=(1/2) + (3/4) + (5/8) + (7/(16)) + ....... = ? Genral term =((1+(n−1)×2)/2^n )=((2n−1)/2^n )=((2n)/2^n )−(1/2^n )=(n/2^(n−1) )−(1/2^n ) So, S=Σ_(n=1) ^(∞) ((n/2^(n−1) )−(1/2^n ))=Σ_(n=1) ^(∞) ((n/2^(n−1) )) −Σ_(n=1) ^(∞) ((1/2^n )) S=((1/2^0 )−(1/2^1 ))+((2/2^1 )−(1/2^2 ))+((3/2^2 )−(1/2^3 ))+((4/2^3 )−(1/2^4 ))+... S=((1/2^0 )+(2/2^1 )+(3/2^2 )+(4/2^3 )+...)−((1/2^1 )+(1/2^2 )+(1/2^3 )+(1/2^4 )+...) S=((1/2^0 )+(2/2^1 )+(3/2^2 )+(4/2^3 )+...)−(((1/2)/(1−(1/2)))) S=(1+(2/2^1 )+(3/2^2 )+(4/2^3 )+...)−1 S=(2/2^1 )+(3/2^2 )+(4/2^3 )+...=(1/2)[(2/2^0 )+(3/2^1 )+(4/2^2 )+...] General term: ((n+1)/2^(n−1) )=(n/2^(n−1) )+(1/2^(n−1) ) S=(1/2)[((1/2^1 )+(2/2^2 )+(3/2^3 )+...)+((1/2^0 )+(1/2^1 )+(1/2^2 )+...)] S=(1/2)[((1/2^0 )+(2/2^1 )+(3/2^2 )+...)+(1/(1−(1/2)))] S=(1/2)[((1/2^0 )+(2/2^1 )+(3/2^2 )+...)+2]>(1/2)[((1/2^0 )+(1/2^1 )+(1/2^2 )+...)+2] S>(1/2)[(1/(1−(1/2)))+2]=(1/2)(2+2)=2 S>2 Continue](Q2942.png)
$${Let}\:{S}=\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{5}}{\mathrm{8}}\:+\:\frac{\mathrm{7}}{\mathrm{16}}\:+\:.......\:=\:\:? \\ $$$$\mathcal{G}{enral}\:{term} \\ $$$$=\frac{\mathrm{1}+\left({n}−\mathrm{1}\right)×\mathrm{2}}{\mathrm{2}^{{n}} }=\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}^{{n}} }=\frac{\mathrm{2}{n}}{\mathrm{2}^{{n}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${So}, \\ $$$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\left(\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left(\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right) \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\right)+\left(\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\right)+\left(\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right)+... \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+...\right)−\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+...\right) \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+...\right)−\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right) \\ $$$${S}=\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+...\right)−\mathrm{1} \\ $$$${S}=\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+...=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{2}} }+...\right] \\ $$$${General}\:{term}:\:\:\:\frac{{n}+\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }=\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+...\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...\right)\right] \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+...\right)+\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right] \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+...\right)+\mathrm{2}\right]>\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...\right)+\mathrm{2}\right] \\ $$$${S}>\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}+\mathrm{2}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{2}\right)=\mathrm{2} \\ $$$${S}>\mathrm{2} \\ $$$${Continue} \\ $$
Commented by Yozzi last updated on 01/Dec/15
$${Let}\:{Q}=\underset{{n}=\mathrm{1}} {\overset{{N}} {\sum}}{nx}^{{n}−\mathrm{1}} =\underset{{n}=\mathrm{1}} {\overset{{N}} {\sum}}\frac{{d}}{{dx}}\left({x}^{{n}} \right)\:\:\left({x}\in\mathbb{R}\right) \\ $$$${Q}=\frac{{d}}{{dx}}\left(\underset{{n}=\mathrm{1}} {\overset{{N}} {\sum}}{x}^{{n}} \right) \\ $$$${Q}=\frac{{d}}{{dx}}\left({x}\underset{{n}=\mathrm{1}} {\overset{{N}} {\sum}}{x}^{{n}−\mathrm{1}} \right) \\ $$$${Q}=\frac{{d}}{{dx}}\left({x}\frac{{x}^{{N}} −\mathrm{1}}{{x}−\mathrm{1}}\right)\:\:\left({x}\neq\mathrm{1}\right) \\ $$$${Q}=\frac{{d}}{{dx}}\left(\frac{{x}^{{N}+\mathrm{1}} −{x}}{{x}−\mathrm{1}}\right) \\ $$$${Q}=\frac{\left({x}−\mathrm{1}\right)\left(\left({N}+\mathrm{1}\right){x}^{{N}} −\mathrm{1}\right)−\left(\mathrm{1}\right)\left({x}^{{N}+\mathrm{1}} −{x}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${Q}=\frac{\left({N}+\mathrm{1}\right){x}^{{N}+\mathrm{1}} −{x}−\left({N}+\mathrm{1}\right){x}^{{N}} +\mathrm{1}−{x}^{{N}+\mathrm{1}} +{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${Q}=\frac{{Nx}^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right){x}^{{N}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${Let}\:{x}=\mathrm{0}.\mathrm{5} \\ $$$$\therefore{Q}=\frac{{N}\left(\mathrm{0}.\mathrm{5}\right)^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right)\left(\mathrm{0}.\mathrm{5}\right)^{{N}} +\mathrm{1}}{\left(\mathrm{0}.\mathrm{5}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${Q}=\mathrm{4}\left({N}\left(\mathrm{0}.\mathrm{5}\right)^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right)\left(\mathrm{0}.\mathrm{5}\right)^{{N}} +\mathrm{1}\right) \\ $$$$\underset{{N}\rightarrow\infty} {\mathrm{lim}}{Q}=\mathrm{4}\left\{\underset{{N}\rightarrow\infty} {\mathrm{lim}}{N}\left(\mathrm{0}.\mathrm{5}\right)^{{N}+\mathrm{1}} −\underset{{N}\rightarrow\infty} {\mathrm{lim}}\left({N}+\mathrm{1}\right)\left(\mathrm{0}.\mathrm{5}\right)^{{N}} +\mathrm{1}\right\} \\ $$$${N}\left(\mathrm{0}.\mathrm{5}\right)^{{N}+\mathrm{1}} =\frac{{N}}{\mathrm{2}^{{N}+\mathrm{1}} }\rightarrow\frac{\infty}{\infty}\:\left({indeterminate}\right) \\ $$$${N}\rightarrow\infty.\:{By}\:{use}\:{of}\:{L}'{Hopital}'{s}\:{rule}, \\ $$$$\underset{{N}\rightarrow\infty} {\mathrm{lim}}\frac{{N}}{\mathrm{2}^{{N}+\mathrm{1}} }=\underset{{N}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}^{{N}+\mathrm{1}} {ln}\mathrm{2}}=\frac{\mathrm{1}}{\infty}=\mathrm{0}\:{and} \\ $$$${similarly}\:\underset{{N}\rightarrow\infty} {\mathrm{lim}}\left({N}+\mathrm{1}\right)\left(\mathrm{0}.\mathrm{5}\right)^{{N}} =\mathrm{0} \\ $$$$\therefore\:\underset{{N}\rightarrow\infty} {\mathrm{lim}}{Q}=\mathrm{4}\left(\mathrm{0}−\mathrm{0}+\mathrm{1}\right)=\mathrm{4} \\ $$$$\Rightarrow{S}=\mathrm{4}−\frac{\mathrm{1}/\mathrm{2}}{\mathrm{1}−\mathrm{0}.\mathrm{5}}=\mathrm{3} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
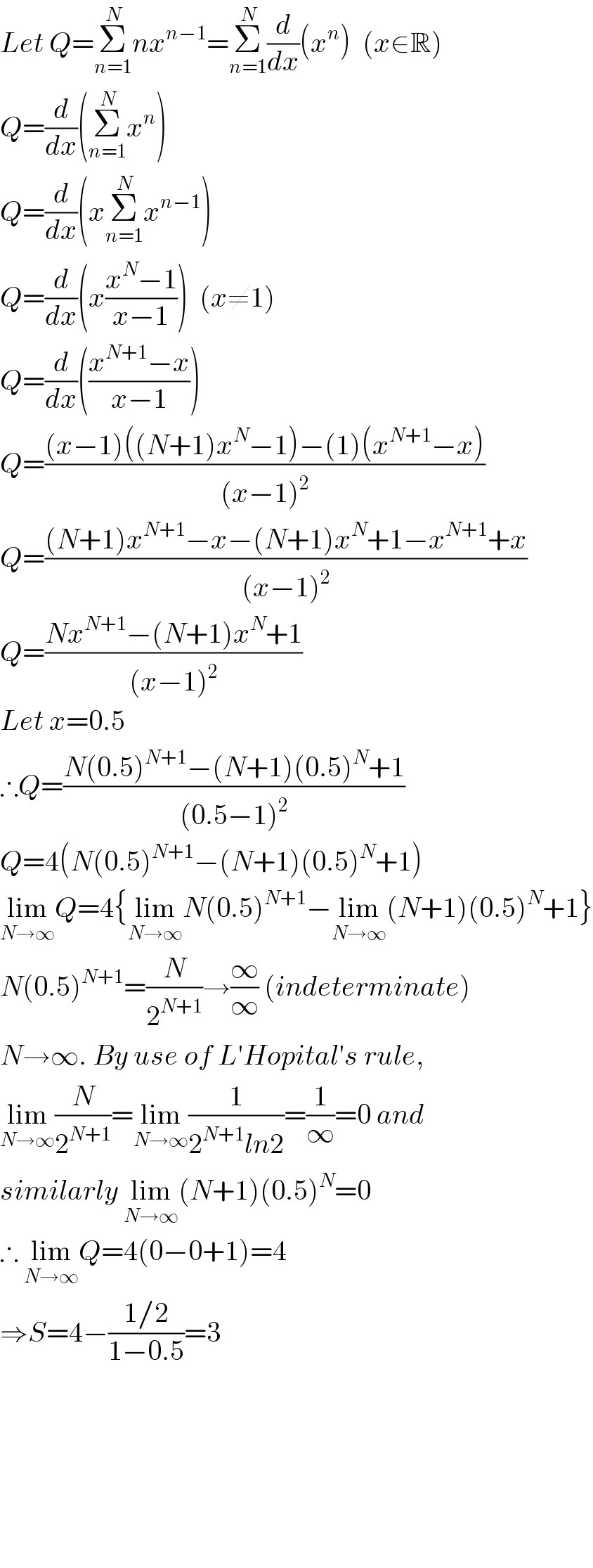
Commented by RasheedAhmad last updated on 02/Dec/15
$${Approach}\:{that}\:{I}\:{couldn}'{t}\:{even}\:{think}\:{of}! \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 03/Dec/15
![Let S=(1/2) + (3/4) + (5/8) + (7/(16)) + ...... General Term:((2n−1)/2^n )=(n/2^(n−1) )−(1/2^n ) S=Σ_(n=1) ^(∞) ((n/2^(n−1) )−(1/2^n ))=Σ_(n=1) ^(∞) ( (n/2^(n−1) ))−Σ_(n=1) ^(∞) ((1/2^n )) =Σ_(n=1) ^(∞) (n((1/2))^(n−1) ) −((1/2)/(1−(1/2))) =Σ_(n=1) ^(∞) (n((1/2))^(n−1) ) −1 With the help of Yozzi ′s comment Let (1/2) (written in red)→x For x=(1/2) : S =Σ_(n=1) ^(∞) (nx^(n−1) )−1 S=−1+Σ_(n=1) ^(∞) (d/dx)(x^n ) S=−1+(d/dx)(lim_(N→∞) Σ_(n=1) ^(N) (x^n )) =−1+lim_(N→∞) [(d/dx)(((x(x^N −1))/(x−1)))] =−1+lim_(N→∞) [(d/dx)(((x^(N+1) −1)/(x−1)))] =−1+lim_(N→∞) [(((x−1)(d/dx)(x^(N+1) −1)−(x^(N+1) −1)(d/dx)(x−1))/((x−1)^2 ))] =−1+lim_(N→∞) [(((x−1)(N+1)x^N −(x^(N+1) −1)(1))/((x−1)^2 ))] =−1+lim_(N→∞) [(((N+1)x^(N+1) −(N+1)x^N −x^(N+1) +1)/((x−1)^2 ))] =−1+lim_(N→∞) [(((N+1)x^(N+1) −x^(N+1) −(N+1)x^N +1)/((x−1)^2 ))] =−1+lim_(N→∞) [(((N+1−1)x^(N+1) −(N+1)x^N +1)/((x−1)^2 ))] =−1+lim_(N→∞) [((Nx^(N+1) −(N+1)x^N +1)/((x−1)^2 ))] ∵ x=(1/2) =−1+lim_(N→∞) [((N((1/2))^(N+1) −(N+1)((1/2))^N +1)/(((1/2)−1)^2 ))] =−1+lim_(N→∞) [((N((1/2))^(N+1) −(N+1)((1/2))^N +1)/(1/4))] =−1+4 lim_(N→∞) [(N/2^(N+1) )−((N+1)/2^N )+1] =−1+4 [lim_(N→∞) (N/2^(N+1) )−lim_(N→∞) ((N+1)/2^N )+lim_(N→∞) 1] By L′Hopital ′s rule lim_(N→∞) (N/2^(N+1) )=0,lim_(N→∞) ((N+1)/2^N )=0 =−1+4(1)=3](Q3032.png)
$${Let} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{5}}{\mathrm{8}}\:+\:\frac{\mathrm{7}}{\mathrm{16}}\:+\:...... \\ $$$$\mathcal{G}{eneral}\:\mathcal{T}{erm}:\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}^{{n}} }=\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left(\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left(\:\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)−\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left({n}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \right)\:−\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\left({n}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \right)\:−\mathrm{1} \\ $$$$\mathcal{W}{ith}\:{the}\:{help}\:{of}\:{Yozzi}\:'{s}\:{comment} \\ $$$${Let}\:\frac{\mathrm{1}}{\mathrm{2}}\:\left({written}\:{in}\:{red}\right)\rightarrow{x} \\ $$$${For}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\:: \\ $$$$\:\:\:\:\:\:{S}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\left({nx}^{{n}−\mathrm{1}} \right)−\mathrm{1}\: \\ $$$$\:\:\:\:\:\:{S}=−\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\:\:\frac{{d}}{{dx}}\left({x}^{{n}} \right) \\ $$$$\:\:\:\:\:\:{S}=−\mathrm{1}+\frac{{d}}{{dx}}\left(\underset{{N}\rightarrow\infty} {{lim}}\underset{{n}=\mathrm{1}} {\overset{{N}} {\Sigma}}\:\:\left({x}^{{n}} \right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{{d}}{{dx}}\left(\frac{{x}\left({x}^{{N}} −\mathrm{1}\right)}{{x}−\mathrm{1}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{{d}}{{dx}}\left(\frac{{x}^{{N}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\:\left[\frac{\left({x}−\mathrm{1}\right)\frac{{d}}{{dx}}\left({x}^{{N}+\mathrm{1}} −\mathrm{1}\right)−\left({x}^{{N}+\mathrm{1}} −\mathrm{1}\right)\frac{{d}}{{dx}}\left({x}−\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{\left({x}−\mathrm{1}\right)\left({N}+\mathrm{1}\right){x}^{{N}} −\left({x}^{{N}+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{\left({N}+\mathrm{1}\right){x}^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right){x}^{{N}} −{x}^{{N}+\mathrm{1}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{\left({N}+\mathrm{1}\right){x}^{{N}+\mathrm{1}} −{x}^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right){x}^{{N}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{\left({N}+\mathrm{1}−\mathrm{1}\right){x}^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right){x}^{{N}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{{Nx}^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right){x}^{{N}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\because\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{{N}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{N}} +\mathrm{1}}{\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:=−\mathrm{1}+\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{{N}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{N}+\mathrm{1}} −\left({N}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{N}} +\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}}\right] \\ $$$$\:\:\:\:=−\mathrm{1}+\mathrm{4}\:\underset{{N}\rightarrow\infty} {{lim}}\left[\frac{{N}}{\mathrm{2}^{{N}+\mathrm{1}} }−\frac{{N}+\mathrm{1}}{\mathrm{2}^{{N}} }+\mathrm{1}\right] \\ $$$$\:\:\:\:=−\mathrm{1}+\mathrm{4}\:\left[\underset{{N}\rightarrow\infty} {{lim}}\frac{{N}}{\mathrm{2}^{{N}+\mathrm{1}} }−\underset{{N}\rightarrow\infty} {{lim}}\frac{{N}+\mathrm{1}}{\mathrm{2}^{{N}} }+\underset{{N}\rightarrow\infty} {{lim}}\mathrm{1}\right] \\ $$$${By}\:{L}'{Hopital}\:'{s}\:{rule}\:\:\underset{{N}\rightarrow\infty} {{lim}}\frac{{N}}{\mathrm{2}^{{N}+\mathrm{1}} }=\mathrm{0},\underset{{N}\rightarrow\infty} {{lim}}\frac{{N}+\mathrm{1}}{\mathrm{2}^{{N}} }=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\mathrm{4}\left(\mathrm{1}\right)=\mathrm{3} \\ $$$$ \\ $$