
Question and Answers Forum
Question Number 29443 by prof Abdo imad last updated on 08/Feb/18
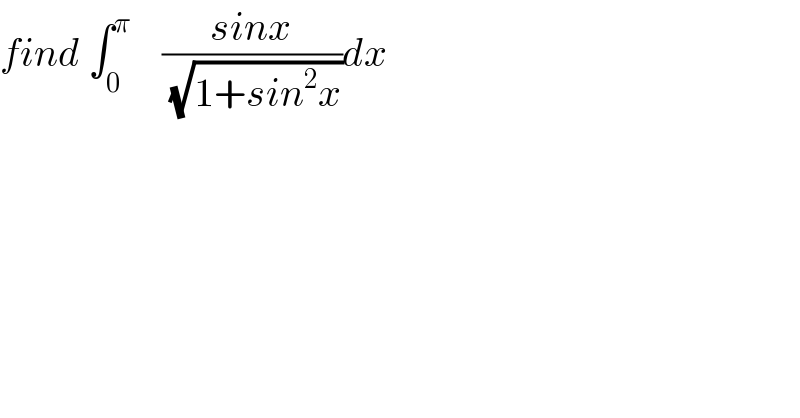
Answered by sma3l2996 last updated on 09/Feb/18
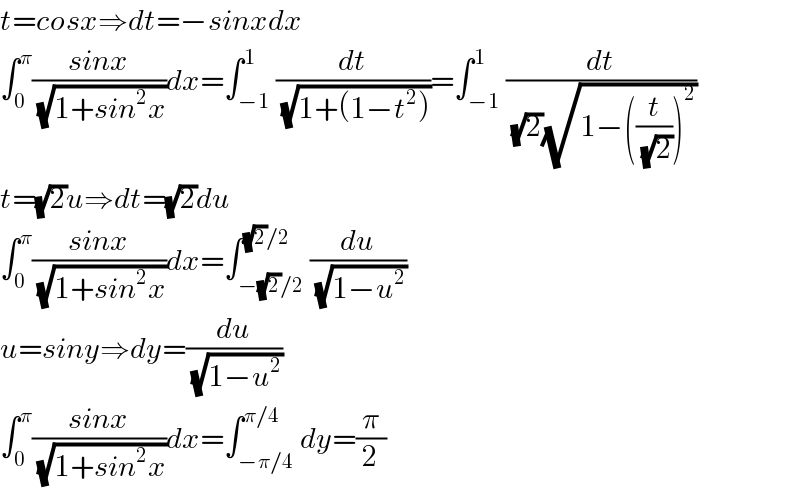
| ||
Question and Answers Forum | ||
Question Number 29443 by prof Abdo imad last updated on 08/Feb/18 | ||
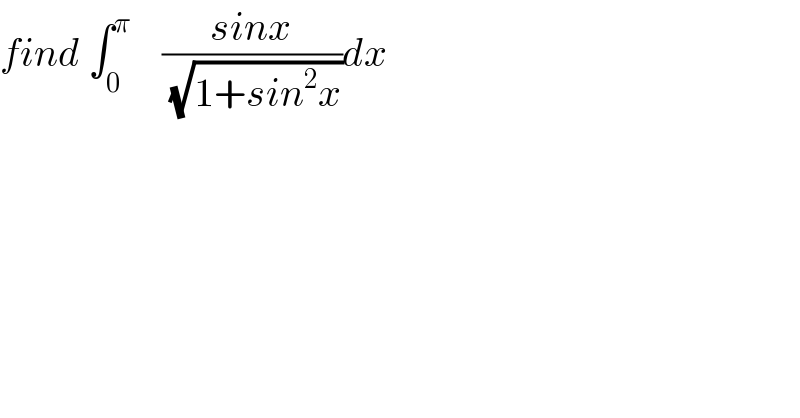 | ||
Answered by sma3l2996 last updated on 09/Feb/18 | ||
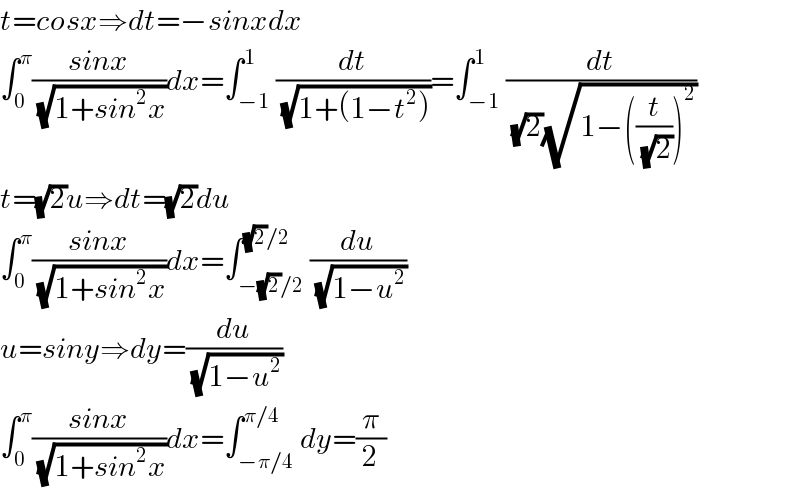 | ||
| ||