
Question Number 29450 by prof Abdo imad last updated on 08/Feb/18
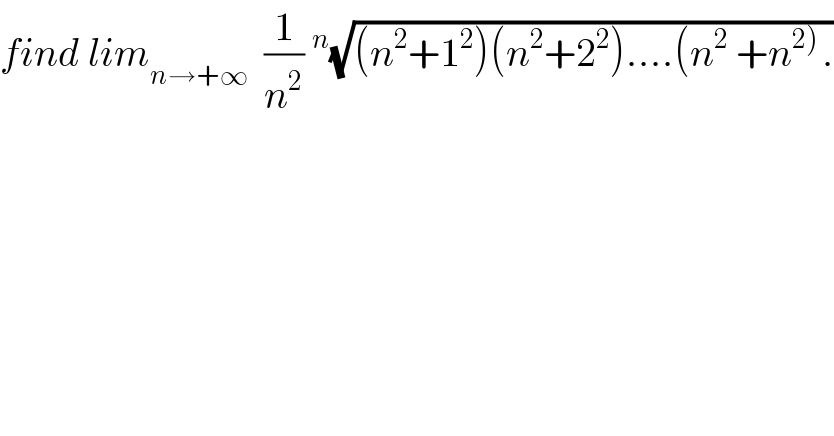
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:^{{n}} \sqrt{\left({n}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \right)\left({n}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right)....\left({n}^{\mathrm{2}} \:+{n}^{\left.\mathrm{2}\right)\:} .\right.} \\ $$
Commented by prof Abdo imad last updated on 23/Mar/18
![let put A_n =(1/n^2 ) ( Π_(k=1) ^n (n^2 +k^2 ))^(1/n) A_n = (1/n^2 )( n^(2n) Π_(k=1) ^n (1+(k^2 /n^2 )))^(1/n) =( Π_(k=1) ^n (1+(k^2 /n^2 ))^(1/n) ⇒ ln(A_n )=(1/n) Σ_(k=1) ^n ln( 1+ ((k/n))^2 )→ ∫_0 ^1 ln(1+x^2 )dx but ∫_0 ^1 ln(1+x^2 )dx= [xln(1+x^2 )]_0 ^1 −∫_0 ^1 ((2x^2 )/(1+x^2 ))dx =ln(2) −2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2) −2 +2 ∫_0 ^1 (dx/(1+x^2 )) =ln(2) −2 + 2 .(π/4) = (π/2) +ln(2) −2 ⇒lim_(n→∞) A_n = e^((π/2) +ln(2)−2) = (2/e^2 ) e^(π/2) .](Q32358.png)
$${let}\:{put}\:\:{A}_{{n}} \:=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:\left(\:\prod_{{k}=\mathrm{1}} ^{{n}} \left({n}^{\mathrm{2}} \:+{k}^{\mathrm{2}} \right)\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${A}_{{n}} =\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\:{n}^{\mathrm{2}{n}} \:\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right)^{\frac{\mathrm{1}}{{n}}} =\left(\:\prod_{{k}=\mathrm{1}} ^{{n}} \:\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{{n}}} \Rightarrow\right. \\ $$$${ln}\left({A}_{{n}} \right)=\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{ln}\left(\:\mathrm{1}+\:\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right)\rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${but}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}=\:\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$={ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:\:+\:\mathrm{2}\:.\frac{\pi}{\mathrm{4}}\:=\:\frac{\pi}{\mathrm{2}}\:+{ln}\left(\mathrm{2}\right)\:−\mathrm{2} \\ $$$$\Rightarrow{lim}_{{n}\rightarrow\infty} \:{A}_{{n}} =\:{e}^{\frac{\pi}{\mathrm{2}}\:+{ln}\left(\mathrm{2}\right)−\mathrm{2}} \:=\:\frac{\mathrm{2}}{{e}^{\mathrm{2}} }\:{e}^{\frac{\pi}{\mathrm{2}}} \:\:. \\ $$
