
Previous in Relation and Functions Next in Relation and Functions
Question Number 29456 by prof Abdo imad last updated on 08/Feb/18
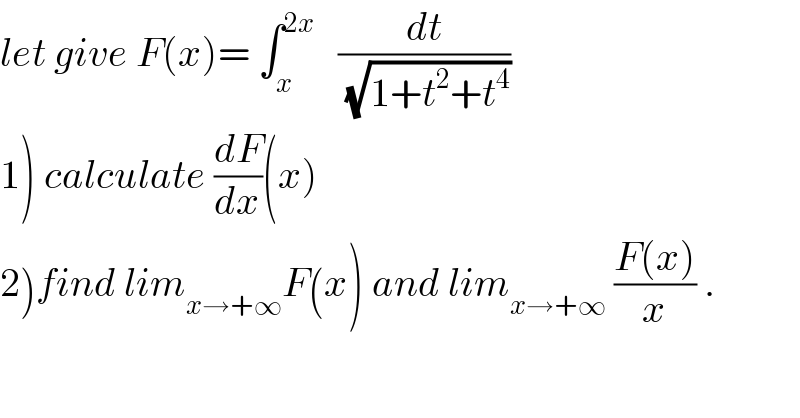
$${let}\:{give}\:{F}\left({x}\right)=\:\int_{{x}} ^{\mathrm{2}{x}} \:\:\:\frac{{dt}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{4}} }}\: \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\frac{{dF}}{{dx}}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{lim}_{{x}\rightarrow+\infty} {F}\left({x}\right)\:{and}\:{lim}_{{x}\rightarrow+\infty} \:\frac{{F}\left({x}\right)}{{x}}\:. \\ $$
Commented by prof Abdo imad last updated on 13/Feb/18
![1) F^′ (x)= (2/(√(1+4x^2 +16x^4 ))) −(1/(√(1+x^2 +x^4 ))) . 2) we have 1 +t^2 +t^4 >t^2 +t^4 ⇒(√(1+t^2 +t^4 >))t(√(1+t^2 )) for t>0 ⇒ (1/(√(1+t^2 +t^4 ))) < (1/(t(√(1+t^2 )))) ⇒ F(x)< ∫_x ^(2x) (dt/(t(√(1+t^2 )))) < ∫_x ^(2x) (dt/t^2 ) =[−(1/t)]_x ^(2x) =(1/x) −(1/(2x)) but lim_(x→+∞ ) ((1/x) −(1/(2x)))=0 ⇒ lim_(x→+∞) F(x)=0 also lim_(x→+∞) ((F(x))/x)=0.](Q29860.png)
$$\left.\mathrm{1}\right)\:{F}^{'} \left({x}\right)=\:\:\:\:\frac{\mathrm{2}}{\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{16}{x}^{\mathrm{4}} }}\:−\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }}\:\:. \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:\:\mathrm{1}\:+{t}^{\mathrm{2}} \:+{t}^{\mathrm{4}} >{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \Rightarrow\sqrt{\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{4}} >}{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${for}\:{t}>\mathrm{0}\:\Rightarrow\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{4}} }}\:<\:\:\:\frac{\mathrm{1}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${F}\left({x}\right)<\:\:\int_{{x}} ^{\mathrm{2}{x}} \:\:\:\:\:\:\:\frac{{dt}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:<\:\int_{{x}} ^{\mathrm{2}{x}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} }\:=\left[−\frac{\mathrm{1}}{{t}}\right]_{{x}} ^{\mathrm{2}{x}} =\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}} \\ $$$${but}\:{lim}_{{x}\rightarrow+\infty\:} \:\:\left(\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}}\right)=\mathrm{0}\:\Rightarrow\:\:{lim}_{{x}\rightarrow+\infty} {F}\left({x}\right)=\mathrm{0} \\ $$$${also}\:{lim}_{{x}\rightarrow+\infty} \:\frac{{F}\left({x}\right)}{{x}}=\mathrm{0}. \\ $$
