
Question and Answers Forum
Question Number 29461 by prof Abdo imad last updated on 09/Feb/18
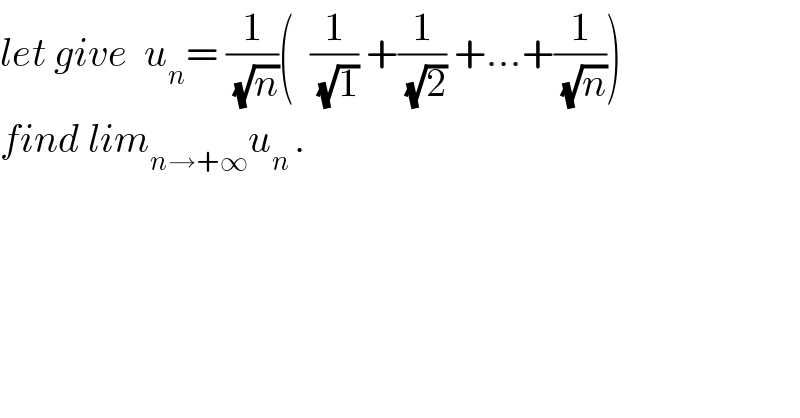
Commented by prof Abdo imad last updated on 13/Feb/18
![we have u_n =((√n)/n)( (1/(√1)) + (1/(√2)) +.....+(1/(√n))) = (1/n)( (1/(√(1/n))) +(1/(√(2/n))) +....+(1/(√(n/n)))) = (1/n)Σ_(k=1) ^n (1/(√(k/n))) so u_(n ) is a Rieman sum and lim_(n→∞) u_n = ∫_0 ^1 (dx/(√x)) =[2(√(x ))]_0 ^1 = 2 .](Q29861.png)
| ||
Question and Answers Forum | ||
Question Number 29461 by prof Abdo imad last updated on 09/Feb/18 | ||
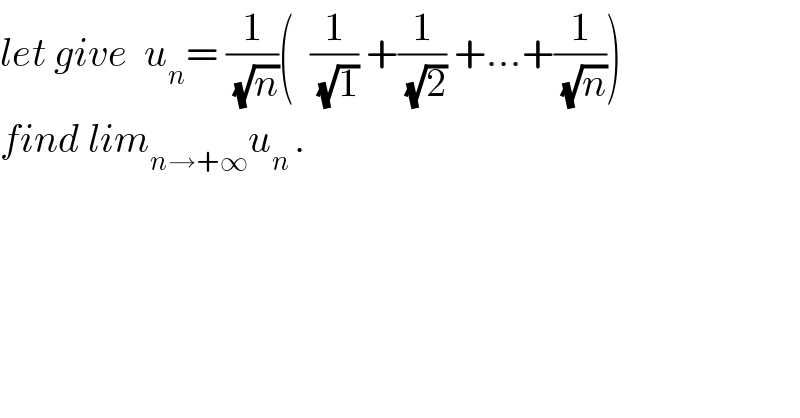 | ||
Commented by prof Abdo imad last updated on 13/Feb/18 | ||
![we have u_n =((√n)/n)( (1/(√1)) + (1/(√2)) +.....+(1/(√n))) = (1/n)( (1/(√(1/n))) +(1/(√(2/n))) +....+(1/(√(n/n)))) = (1/n)Σ_(k=1) ^n (1/(√(k/n))) so u_(n ) is a Rieman sum and lim_(n→∞) u_n = ∫_0 ^1 (dx/(√x)) =[2(√(x ))]_0 ^1 = 2 .](Q29861.png) | ||