
Question and Answers Forum
Question Number 29574 by yesasitya22@gmail.com last updated on 10/Feb/18
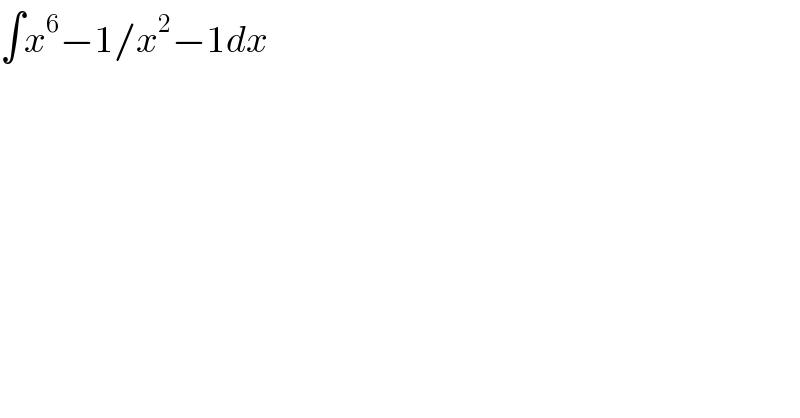
Commented by tawa tawa last updated on 10/Feb/18
![∫ ((x^6 − 1)/(x^2 − 1)) dx = ∫ (((x^2 )^3 − 1^3 )/(x^2 − 1)) dx Simplify the numerator using the identity: x^3 − y^3 = (x − y)(x^2 + xy + y^2 ) = ∫ (((x^2 − 1)[(x^2 )^2 + x^2 + 1^2 ])/(x^2 − 1)) dx = ∫ (((x^2 − 1)(x^4 + x^2 + 1))/(x^2 − 1)) dx = ∫ (x^4 + x^2 + 1) dx = (x^5 /5) + (x^3 /3) + x + C = (1/5) x^5 + (1/3) x^3 + x + C](Q29625.png)
Commented by ajfour last updated on 10/Feb/18

| ||
Question and Answers Forum | ||
Question Number 29574 by yesasitya22@gmail.com last updated on 10/Feb/18 | ||
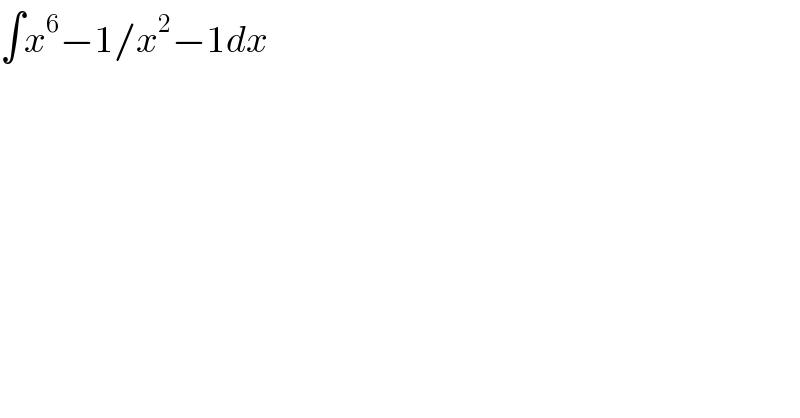 | ||
Commented by tawa tawa last updated on 10/Feb/18 | ||
![∫ ((x^6 − 1)/(x^2 − 1)) dx = ∫ (((x^2 )^3 − 1^3 )/(x^2 − 1)) dx Simplify the numerator using the identity: x^3 − y^3 = (x − y)(x^2 + xy + y^2 ) = ∫ (((x^2 − 1)[(x^2 )^2 + x^2 + 1^2 ])/(x^2 − 1)) dx = ∫ (((x^2 − 1)(x^4 + x^2 + 1))/(x^2 − 1)) dx = ∫ (x^4 + x^2 + 1) dx = (x^5 /5) + (x^3 /3) + x + C = (1/5) x^5 + (1/3) x^3 + x + C](Q29625.png) | ||
Commented by ajfour last updated on 10/Feb/18 | ||
 | ||