Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 29633 by Tinkutara last updated on 10/Feb/18

Commented by Tinkutara last updated on 10/Feb/18
http://ibb.co/cyaemS
Commented by 33 last updated on 11/Feb/18

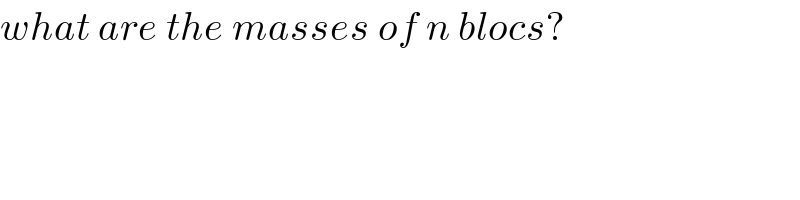
$w h a t a r e t h e m a s s e s o f n b l o c s ?$
Commented by mrW2 last updated on 11/Feb/18

$J u s t a t h o u g h t, n o t a p r o o f :$ $m a x . p o s s i b l e s p e e d o f l a s t m a s s m_{2} :$ $u = v {[\frac{2}{1 + {(\frac{m_{2}}{m_{1}})}^{\frac{1}{n + 1}}}]}^{n + 1}$ $e . g . m_{2} = 2 m_{1}, n = 10 :$ $u \approx 0.703 v$ $e . g . m_{2} = 0.5 m_{1}, n = 10 :$ $u \approx 1.406 v$ $\lim_{n \to \infty} u = \sqrt{\frac{m_{1}}{m_{2}}} v$ $t h i s i s t h e m a x . p o s s i b l e s p e e d w h i c h$ $t h e m a s s m_{2} c a n a c h i e v e b y p l a c e i n g$ $i n f i n i t e l y m a n y b l o c k s b e t w e e n m_{1}$ $a n d m_{2} .$
Commented by Tinkutara last updated on 11/Feb/18

Commented by Tinkutara last updated on 11/Feb/18
This is the answer. I am getting a slightly different one. I am not getting any exponent of a in numerator rest is the same.
Commented by 33 last updated on 11/Feb/18

$w h a t a r e t h e m a s s e s o f n b l o c s$ $a n y i n f o g i v e n . p l z t e l l ?$
Commented by Tinkutara last updated on 11/Feb/18
Masses of all blocks are different.
Commented by Tinkutara last updated on 11/Feb/18

$B u t a n s w e r s h o u l d b e \frac{2^{n + 1} v}{{(1 + a)}^{n + 1}} o r$ $y o u a r e g e t t i n g a n o t h e r a n s w e r ?$
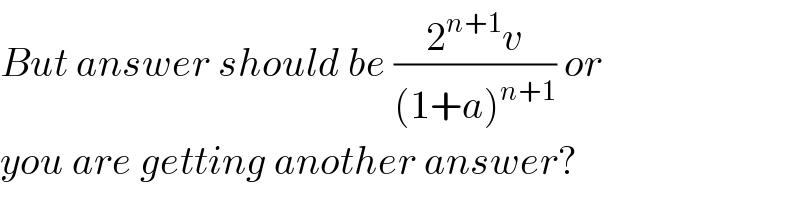
Commented by mrW2 last updated on 11/Feb/18

$Y e s, a n s w e r s h o u l d b e \frac{2^{n + 1} v}{{(1 + a)}^{n + 1}}, t h i s$ $i s a l s o m y a n s w e r . B u t t h e a n s w e r y o u$ $g a v e f r o m t h e b o o k i s$ $\frac{2^{n + 1} a^{\frac{n (n - 1)}{2}} v}{{(1 + a)}^{n + 1}} . T h i s i s n o t c o r r e c t, I t h i n k .$
Commented by Tinkutara last updated on 11/Feb/18
Thanks! I got it now. ��☺
	Answered by mrW2 last updated on 12/Feb/18
	$We have totally n+1 masses: M_0 , M_1 ,M_2 ,...,M_n ,M_(n+1) with M_0 =m_1 and M_(n+1) =m_2 . M_1 ,M_2 ,...,M_n are unknown and may be freely determined. For mass M_i (i=0,1,2,...,n+1) let′s assume: v_(i,1) =speed after collision with M_(i−1) v_(i,2) =speed after collision with M_(i+1) v_(0,1) =V_1 =initial speed of first mass m_1 v_(n+1,1) =V_2 =final speed of last mass m_2 Collision M_i with M_(i+1) (perfectly elastic): M_i v_(i,1) =M_i v_(i,2) +M_(i+1) v_(i+1,1) ⇒M_i (v_(i,1) −v_(i,2) )=M_(i+1) v_(i+1,1) ...(i) (1/2)M_i v_(i,1) ^2 =(1/2)M_i v_(i,2) ^2 +(1/2)M_(i+1) v_(i+1,1) ^2 ⇒M_i (v_(i,1) ^2 −v_(i,2) ^2 )=M_(i+1) v_(i+1,1) ^2 ...(ii) (ii)/(i): ⇒v_(i,1) +v_(i,2) =v_(i+1,1) take this into (i): ⇒M_i (2v_(i,1) −v_(i+1,1) )=M_(i+1) v_(i+1,1) ⇒2M_i v_(i,1) =(M_i +M_(i+1) )v_(i+1,1) ⇒(v_(i+1,1) /v_(i,1) )=(2/(1+(M_(i+1) /M_i ))) (v_(1,1) /v_(0,1) )×(v_(2,1) /v_(1,1) )×...×(v_(n+1,1) /v_(n,1) )=(2/(1+(M_1 /M_0 )))×(2/(1+(M_2 /M_1 )))×...×(2/(1+(M_(n+1) /M_n ))) ⇒(v_(n+1,1) /v_(0,1) )=(2^(n+1) /((1+(M_1 /M_0 ))(1+(M_2 /M_1 ))...(1+(M_(n+1) /M_n )))) ⇒(V_2 /V_1 )=(2^(n+1) /((1+(M_1 /M_0 ))(1+(M_2 /M_1 ))...(1+(M_(n+1) /M_n ))))=2^(n+1) F(M_1 ,M_2 ,...,M_n ) with F(M_1 ,M_2 ,...,M_n )=(1/((1+(M_1 /M_0 ))(1+(M_2 /M_1 ))...(1+(M_(n+1) /M_n )))) or F(M_1 ,M_2 ,...,M_n )=((M_0 M_1 M_2 ...M_n )/((M_0 +M_1 )(M_1 +M_2 )...(M_n +M_(n+1) ))) (∂F/∂M_i )=((M_0 M_1 M_2 ...M_n )/((M_0 +M_1 )(M_1 +M_2 )...(M_n +M_(n+1) )M_i ))−((M_0 M_1 M_2 ...M_n (M_(i−1) +M_i +M_i +M_(i+1) ))/((M_0 +M_1 )(M_1 +M_2 )...(M_n +M_(n+1) )(M_(i−1) +M_i )(M_i +M_(i+1) ))) (∂F/∂M_i )=F(M_1 ,M_2 ,...,M_n ){(1/M_i )−((M_(i−1) +2M_i +M_(i+1) )/((M_(i−1) +M_i )(M_i +M_(i+1) )))} (∂F/∂M_i )=F(M_1 ,M_2 ,...,M_n ){((M_(i−1) M_i +M_i ^2 +M_(i−1) M_(i+1) +M_i M_(i+1) −M_(i−1) M_i −2M_i ^2 −M_i M_(i+1) )/(M_i (M_(i−1) +M_i )(M_i +M_(i+1) )))} (∂F/∂M_i )=F(M_1 ,M_2 ,...,M_n ){((M_(i−1) M_(i+1) −M_i ^2 )/(M_i (M_(i−1) +M_i )(M_i +M_(i+1) )))} For F(M_1 ,M_2 ,...,M_n ) to be maximum, (∂F/∂M_i )=0, i=1,2,..,n ⇒M_(i−1) M_(i+1) −M_i ^2 =0 ⇒(M_i /M_(i−1) )=(M_(i+1) /M_i ), i=1,2,..,n i.e. M_0 , M_1 ,M_2 ,...,M_n ,M_(n+1) must buid a G.P. to get maximum for (V_2 /V_1 ), i.e. (M_1 /M_0 )=(M_2 /M_1 )=...=(M_(n+1) /M_n )=a (say) ⇒(M_1 /M_0 )×(M_2 /M_1 )×(M_3 /M_2 )×...×(M_(n+1) /M_n )=a^(n+1) ⇒(M_(n+1) /M_0 )=a^(n+1) =(m_2 /m_1 ) ⇒a=((m_2 /m_1 ))^(1/(n+1)) ⇒((V_2 /V_1 ))_(max) =(2^(n+1) /((1+a)^(n+1) )) =((2/(1+a)))^(n+1) ⇒max. V_2 =[(2/(1+((m_2 /m_1 ))^(1/(n+1)) ))]^(n+1) V_1$
	$W e h a v e t o t a l l y n + 1 m a s s e s :$ $M_{0}, M_{1}, M_{2}, . . ., M_{n}, M_{n + 1}$ $w i t h M_{0} = m_{1} a n d M_{n + 1} = m_{2} .$ $M_{1}, M_{2}, . . ., M_{n} a r e u n k n o w n a n d m a y$ $b e f r e e l y d e t e r m i n e d .$ $F o r m a s s M_{i} (i = 0, 1, 2, . . ., n + 1) {l e t}^{'} s$ $a s s u m e :$ $v_{i, 1} = s p e e d a f t e r c o l l i s i o n w i t h M_{i - 1}$ $v_{i, 2} = s p e e d a f t e r c o l l i s i o n w i t h M_{i + 1}$ $v_{0, 1} = V_{1} = i n i t i a l s p e e d o f f i r s t m a s s m_{1}$ $v_{n + 1, 1} = V_{2} = f i n a l s p e e d o f l a s t m a s s m_{2}$ $C o l l i s i o n M_{i} w i t h M_{i + 1} (p e r f e c t l y e l a s t i c) :$ $M_{i} v_{i, 1} = M_{i} v_{i, 2} + M_{i + 1} v_{i + 1, 1}$ $\Rightarrow M_{i} (v_{i, 1} - v_{i, 2}) = M_{i + 1} v_{i + 1, 1} . . . (i)$ $\frac{1}{2} M_{i} v_{i, 1}^{2} = \frac{1}{2} M_{i} v_{i, 2}^{2} + \frac{1}{2} M_{i + 1} v_{i + 1, 1}^{2}$ $\Rightarrow M_{i} (v_{i, 1}^{2} - v_{i, 2}^{2}) = M_{i + 1} v_{i + 1, 1}^{2} . . . (i i)$ $(i i) / (i) :$ $\Rightarrow v_{i, 1} + v_{i, 2} = v_{i + 1, 1}$ $t a k e t h i s i n t o (i) :$ $\Rightarrow M_{i} (2 v_{i, 1} - v_{i + 1, 1}) = M_{i + 1} v_{i + 1, 1}$ $\Rightarrow 2 M_{i} v_{i, 1} = (M_{i} + M_{i + 1}) v_{i + 1, 1}$ $\Rightarrow \frac{v_{i + 1, 1}}{v_{i, 1}} = \frac{2}{1 + \frac{M_{i + 1}}{M_{i}}}$ $\frac{v_{1, 1}}{v_{0, 1}} \times \frac{v_{2, 1}}{v_{1, 1}} \times . . . \times \frac{v_{n + 1, 1}}{v_{n, 1}} = \frac{2}{1 + \frac{M_{1}}{M_{0}}} \times \frac{2}{1 + \frac{M_{2}}{M_{1}}} \times . . . \times \frac{2}{1 + \frac{M_{n + 1}}{M_{n}}}$ $\Rightarrow \frac{v_{n + 1, 1}}{v_{0, 1}} = \frac{2^{n + 1}}{(1 + \frac{M_{1}}{M_{0}}) (1 + \frac{M_{2}}{M_{1}}) . . . (1 + \frac{M_{n + 1}}{M_{n}})}$ $\Rightarrow \frac{V_{2}}{V_{1}} = \frac{2^{n + 1}}{(1 + \frac{M_{1}}{M_{0}}) (1 + \frac{M_{2}}{M_{1}}) . . . (1 + \frac{M_{n + 1}}{M_{n}})} = 2^{n + 1} F (M_{1}, M_{2}, . . ., M_{n})$ $w i t h$ $F (M_{1}, M_{2}, . . ., M_{n}) = \frac{1}{(1 + \frac{M_{1}}{M_{0}}) (1 + \frac{M_{2}}{M_{1}}) . . . (1 + \frac{M_{n + 1}}{M_{n}})}$ $o r$ $F (M_{1}, M_{2}, . . ., M_{n}) = \frac{M_{0} M_{1} M_{2} . . . M_{n}}{(M_{0} + M_{1}) (M_{1} + M_{2}) . . . (M_{n} + M_{n + 1})}$ $\frac{\partial F}{\partial M_{i}} = \frac{M_{0} M_{1} M_{2} . . . M_{n}}{(M_{0} + M_{1}) (M_{1} + M_{2}) . . . (M_{n} + M_{n + 1}) M_{i}} - \frac{M_{0} M_{1} M_{2} . . . M_{n} (M_{i - 1} + M_{i} + M_{i} + M_{i + 1})}{(M_{0} + M_{1}) (M_{1} + M_{2}) . . . (M_{n} + M_{n + 1}) (M_{i - 1} + M_{i}) (M_{i} + M_{i + 1})}$ $\frac{\partial F}{\partial M_{i}} = F (M_{1}, M_{2}, . . ., M_{n}) {\frac{1}{M_{i}} - \frac{M_{i - 1} + 2 M_{i} + M_{i + 1}}{(M_{i - 1} + M_{i}) (M_{i} + M_{i + 1})}}$ $\frac{\partial F}{\partial M_{i}} = F (M_{1}, M_{2}, . . ., M_{n}) {\frac{M_{i - 1} M_{i} + M_{i}^{2} + M_{i - 1} M_{i + 1} + M_{i} M_{i + 1} - M_{i - 1} M_{i} - 2 M_{i}^{2} - M_{i} M_{i + 1}}{M_{i} (M_{i - 1} + M_{i}) (M_{i} + M_{i + 1})}}$ $\frac{\partial F}{\partial M_{i}} = F (M_{1}, M_{2}, . . ., M_{n}) {\frac{M_{i - 1} M_{i + 1} - M_{i}^{2}}{M_{i} (M_{i - 1} + M_{i}) (M_{i} + M_{i + 1})}}$ $F o r F (M_{1}, M_{2}, . . ., M_{n}) t o b e m a x i m u m, \frac{\partial F}{\partial M_{i}} = 0, i = 1, 2, . ., n$ $\Rightarrow M_{i - 1} M_{i + 1} - M_{i}^{2} = 0$ $\Rightarrow \frac{M_{i}}{M_{i - 1}} = \frac{M_{i + 1}}{M_{i}}, i = 1, 2, . ., n$ $i . e . M_{0}, M_{1}, M_{2}, . . ., M_{n}, M_{n + 1} m u s t b u i d$ $a G . P . t o g e t m a x i m u m f o r \frac{V_{2}}{V_{1}},$ $i . e . \frac{M_{1}}{M_{0}} = \frac{M_{2}}{M_{1}} = . . . = \frac{M_{n + 1}}{M_{n}} = a (s a y)$ $\Rightarrow \frac{M_{1}}{M_{0}} \times \frac{M_{2}}{M_{1}} \times \frac{M_{3}}{M_{2}} \times . . . \times \frac{M_{n + 1}}{M_{n}} = a^{n + 1}$ $\Rightarrow \frac{M_{n + 1}}{M_{0}} = a^{n + 1} = \frac{m_{2}}{m_{1}}$ $\Rightarrow a = {(\frac{m_{2}}{m_{1}})}^{\frac{1}{n + 1}}$ $\Rightarrow {(\frac{V_{2}}{V_{1}})}_{m a x} = \frac{2^{n + 1}}{{(1 + a)}^{n + 1}} = {(\frac{2}{1 + a})}^{n + 1}$ $\Rightarrow m a x . V_{2} = {[\frac{2}{1 + {(\frac{m_{2}}{m_{1}})}^{\frac{1}{n + 1}}}]}^{n + 1} V_{1}$
	Commented by Tinkutara last updated on 11/Feb/18
	How can you say that maximum occurs when masses are in GP? It also requires a proof.
	Commented by mrW2 last updated on 11/Feb/18
	I have added the proof. But that was obvious.
	Commented by Tinkutara last updated on 11/Feb/18
	Thanks but we can also maximize the expression of velocity acquired by last block when there are 3 such different blocks to get relation.
	Commented by mrW2 last updated on 11/Feb/18

	${T h a t}^{'} s p o s s i b l e a n d e a s i e r . I w a n t e d a$ $g e n e r a l s o l u t i o n f o r a n y n u m b e r o f$ $b l o c k s .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum