Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2980 by Filup last updated on 02/Dec/15

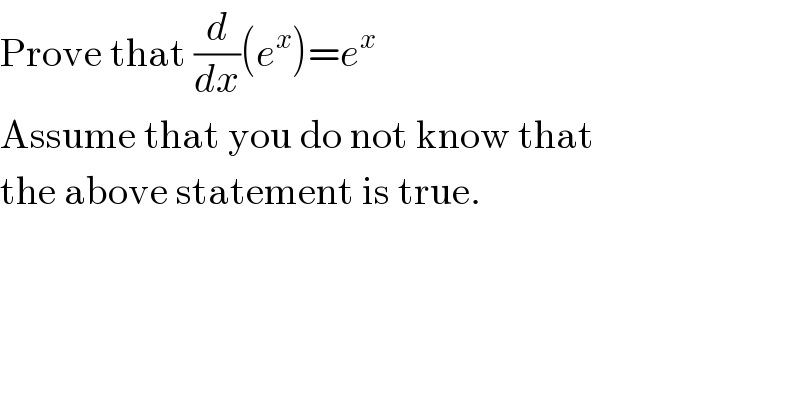
Prove that (d/dx)(e^x )=e^x Assume that you do not know that the above statement is true.

$$\mathrm{Prove}\:\mathrm{that}\:\frac{{d}}{{dx}}\left({e}^{{x}} \right)={e}^{{x}} \\ $$$$\mathrm{Assume}\:\mathrm{that}\:\mathrm{you}\:\mathrm{do}\:\mathrm{not}\:\mathrm{know}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{above}\:\mathrm{statement}\:\mathrm{is}\:\mathrm{true}. \\ $$

Answered by RasheedAhmad last updated on 02/Dec/15

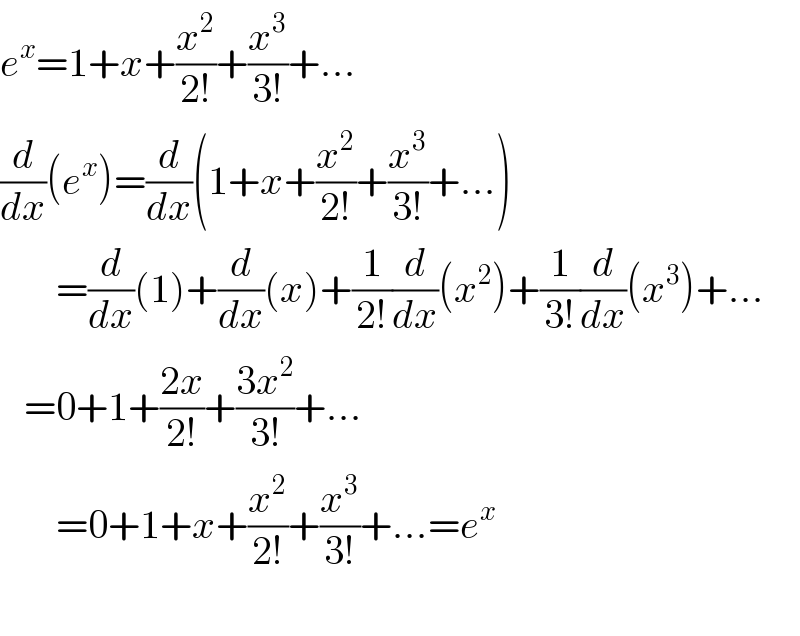
e^x =1+x+(x^2 /(2!))+(x^3 /(3!))+... (d/dx)(e^x )=(d/dx)(1+x+(x^2 /(2!))+(x^3 /(3!))+...) =(d/dx)(1)+(d/dx)(x)+(1/(2!))(d/dx)(x^2 )+(1/(3!))(d/dx)(x^3 )+... =0+1+((2x)/(2!))+((3x^2 )/(3!))+... =0+1+x+(x^2 /(2!))+(x^3 /(3!))+...=e^x

$${e}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+... \\ $$$$\frac{{d}}{{dx}}\left({e}^{{x}} \right)=\frac{{d}}{{dx}}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+...\right) \\ $$$$\:\:\:\:\:\:\:=\frac{{d}}{{dx}}\left(\mathrm{1}\right)+\frac{{d}}{{dx}}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}!}\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{3}!}\frac{{d}}{{dx}}\left({x}^{\mathrm{3}} \right)+... \\ $$$$\:\:\:=\mathrm{0}+\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{2}!}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{3}!}+... \\ $$$$\:\:\:\:\:\:\:=\mathrm{0}+\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+...={e}^{{x}} \\ $$$$ \\ $$

Answered by 123456 last updated on 02/Dec/15

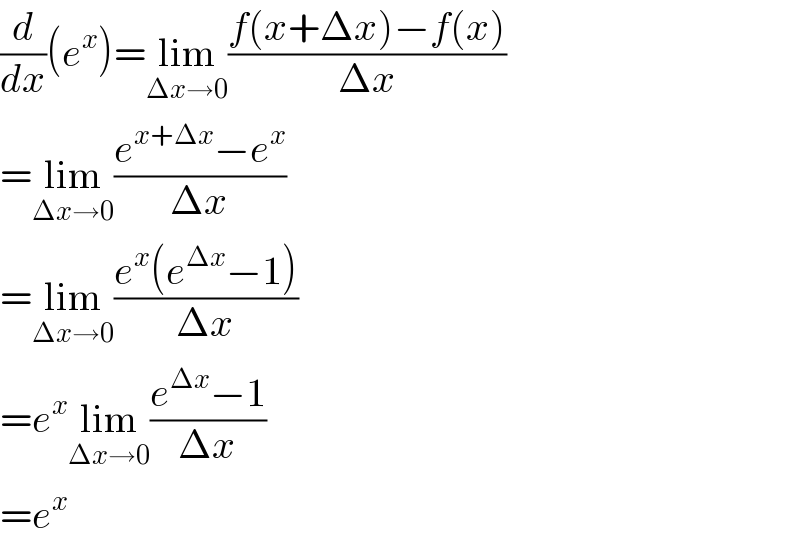
(d/dx)(e^x )=lim_(Δx→0) ((f(x+Δx)−f(x))/(Δx)) =lim_(Δx→0) ((e^(x+Δx) −e^x )/(Δx)) =lim_(Δx→0) ((e^x (e^(Δx) −1))/(Δx)) =e^x lim_(Δx→0) ((e^(Δx) −1)/(Δx)) =e^x

$$\frac{{d}}{{dx}}\left({e}^{{x}} \right)=\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+\Delta{x}\right)−{f}\left({x}\right)}{\Delta{x}} \\ $$$$=\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}+\Delta{x}} −{e}^{{x}} }{\Delta{x}} \\ $$$$=\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} \left({e}^{\Delta{x}} −\mathrm{1}\right)}{\Delta{x}} \\ $$$$={e}^{{x}} \underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\Delta{x}} −\mathrm{1}}{\Delta{x}} \\ $$$$={e}^{{x}} \\ $$

Commented by 123456 last updated on 02/Dec/15

lim_(x→0) ((a^x −1)/x)=ln a

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}^{{x}} −\mathrm{1}}{{x}}=\mathrm{ln}\:{a} \\ $$

Commented by Filup last updated on 02/Dec/15

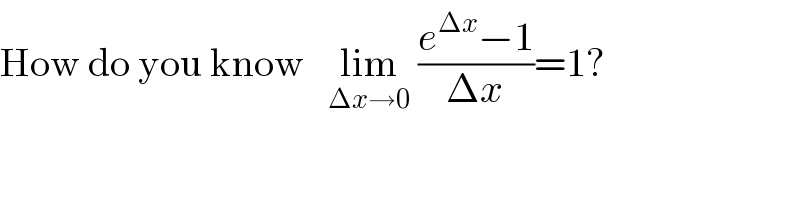
How do you know lim_(Δx→0) ((e^(Δx) −1)/(Δx))=1?

$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\:\:\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{\Delta{x}} −\mathrm{1}}{\Delta{x}}=\mathrm{1}? \\ $$

Commented by Yozzi last updated on 03/Dec/15

Let lim_(Δx→0) ((e^(Δx) −1)/(Δx))=l. Using the Maclaurin series expansion for e^(Δx ) we have e^(Δx) =1+Δx+(((Δx)^2 )/2)+(((Δx)^3 )/6)+(((Δx)^4 )/(24))+... ⇒e^(Δx) −1=Σ_(r=1) ^∞ (((Δx)^r )/(r!)) ⇒((e^(Δx) −1)/(Δx))=Σ_(r=1) ^∞ (((Δx)^(r−1) )/(r!)) So, lim_(Δx→0) ((e^(Δx) −1)/(Δx))=lim_(Δx→0) Σ_(r=1) ^∞ (((Δx)^(r−1) )/(r!)) l=lim_(Δx→0) (1/1)+Σ_(r=2) ^∞ (((Δx)^(r−1) )/(r!))

$${Let}\:\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\Delta{x}} −\mathrm{1}}{\Delta{x}}={l}.\:{Using}\:{the}\:{Maclaurin} \\ $$$${series}\:{expansion}\:{for}\:{e}^{\Delta{x}\:} {we}\:{have} \\ $$$${e}^{\Delta{x}} =\mathrm{1}+\Delta{x}+\frac{\left(\Delta{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\Delta{x}\right)^{\mathrm{3}} }{\mathrm{6}}+\frac{\left(\Delta{x}\right)^{\mathrm{4}} }{\mathrm{24}}+... \\ $$$$\Rightarrow{e}^{\Delta{x}} −\mathrm{1}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\Delta{x}\right)^{{r}} }{{r}!} \\ $$$$\Rightarrow\frac{{e}^{\Delta{x}} −\mathrm{1}}{\Delta{x}}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\Delta{x}\right)^{{r}−\mathrm{1}} }{{r}!} \\ $$$${So},\:\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\Delta{x}} −\mathrm{1}}{\Delta{x}}=\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\Delta{x}\right)^{{r}−\mathrm{1}} }{{r}!} \\ $$$${l}=\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}}+\underset{{r}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(\Delta{x}\right)^{{r}−\mathrm{1}} }{{r}!} \\ $$$$ \\ $$

Commented by Filup last updated on 03/Dec/15

Thats true, but to derive thus series you must take the derivative of e^x ...?

$$\mathrm{Thats}\:\mathrm{true},\:{but}\:\mathrm{to}\:\mathrm{derive}\:\mathrm{thus}\:\mathrm{series}\:\mathrm{you} \\ $$$$\mathrm{must}\:\mathrm{take}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{of}\:{e}^{{x}} ...? \\ $$

Commented by Yozzi last updated on 03/Dec/15

Yes. You′re right. Perhaps then another a method of proof of lim_(x→0) ((e^x −1)/x)=1 is required that is devoid of differentiating e^x . It means then that the first answer is not what you want since it is a series based on (d/dx)(e^x ).

$${Yes}.\:{You}'{re}\:{right}.\:{Perhaps}\:{then}\:{another} \\ $$$${a}\:{method}\:{of}\:{proof}\:{of}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}=\mathrm{1} \\ $$$${is}\:{required}\:{that}\:{is}\:{devoid}\:{of}\: \\ $$$${differentiating}\:{e}^{{x}} . \\ $$$${It}\:{means}\:{then}\:{that}\:{the}\:{first}\:{answer} \\ $$$${is}\:{not}\:{what}\:{you}\:{want}\:{since}\:{it}\:{is}\:{a}\:{series} \\ $$$${based}\:{on}\:\frac{{d}}{{dx}}\left({e}^{{x}} \right).\: \\ $$

Commented by Yozzi last updated on 03/Dec/15

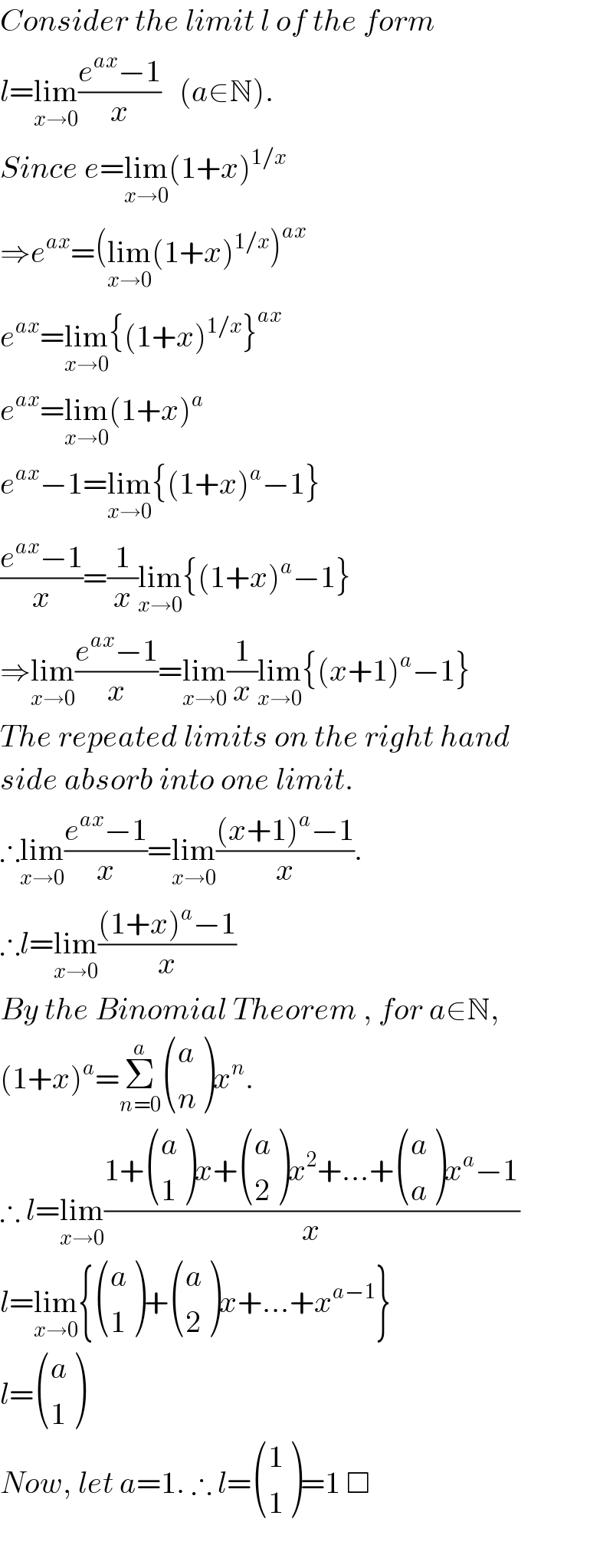
Consider the limit l of the form l=lim_(x→0) ((e^(ax) −1)/x) (a∈N). Since e=lim_(x→0) (1+x)^(1/x) ⇒e^(ax) =(lim_(x→0) (1+x)^(1/x) )^(ax) e^(ax) =lim_(x→0) {(1+x)^(1/x) }^(ax) e^(ax) =lim_(x→0) (1+x)^a e^(ax) −1=lim_(x→0) {(1+x)^a −1} ((e^(ax) −1)/x)=(1/x)lim_(x→0) {(1+x)^a −1} ⇒lim_(x→0) ((e^(ax) −1)/x)=lim_(x→0) (1/x)lim_(x→0) {(x+1)^a −1} The repeated limits on the right hand side absorb into one limit. ∴lim_(x→0) ((e^(ax) −1)/x)=lim_(x→0) (((x+1)^a −1)/x). ∴l=lim_(x→0) (((1+x)^a −1)/x) By the Binomial Theorem , for a∈N, (1+x)^a =Σ_(n=0) ^a ((a),(n) )x^n . ∴ l=lim_(x→0) ((1+ ((a),(1) )x+ ((a),(2) )x^2 +...+ ((a),(a) )x^a −1)/x) l=lim_(x→0) { ((a),(1) )+ ((a),(2) )x+...+x^(a−1) } l= ((a),(1) ) Now, let a=1. ∴ l= ((1),(1) )=1 □

$${Consider}\:{the}\:{limit}\:{l}\:{of}\:{the}\:{form} \\ $$$${l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{ax}} −\mathrm{1}}{{x}}\:\:\:\left({a}\in\mathbb{N}\right). \\ $$$${Since}\:{e}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} \\ $$$$\Rightarrow{e}^{{ax}} =\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} \right)^{{ax}} \\ $$$${e}^{{ax}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} \right\}^{{ax}} \\ $$$${e}^{{ax}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{{a}} \\ $$$${e}^{{ax}} −\mathrm{1}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left(\mathrm{1}+{x}\right)^{{a}} −\mathrm{1}\right\} \\ $$$$\frac{{e}^{{ax}} −\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{x}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left(\mathrm{1}+{x}\right)^{{a}} −\mathrm{1}\right\} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{ax}} −\mathrm{1}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left({x}+\mathrm{1}\right)^{{a}} −\mathrm{1}\right\} \\ $$$${The}\:{repeated}\:{limits}\:{on}\:{the}\:{right}\:{hand} \\ $$$${side}\:{absorb}\:{into}\:{one}\:{limit}. \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{ax}} −\mathrm{1}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)^{{a}} −\mathrm{1}}{{x}}. \\ $$$$\therefore{l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+{x}\right)^{{a}} −\mathrm{1}}{{x}} \\ $$$${By}\:{the}\:{Binomial}\:{Theorem}\:,\:{for}\:{a}\in\mathbb{N}, \\ $$$$\left(\mathrm{1}+{x}\right)^{{a}} =\underset{{n}=\mathrm{0}} {\overset{{a}} {\sum}}\begin{pmatrix}{{a}}\\{{n}}\end{pmatrix}{x}^{{n}} . \\ $$$$\therefore\:{l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\begin{pmatrix}{{a}}\\{\mathrm{1}}\end{pmatrix}{x}+\begin{pmatrix}{{a}}\\{\mathrm{2}}\end{pmatrix}{x}^{\mathrm{2}} +...+\begin{pmatrix}{{a}}\\{{a}}\end{pmatrix}{x}^{{a}} −\mathrm{1}}{{x}} \\ $$$${l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\begin{pmatrix}{{a}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{a}}\\{\mathrm{2}}\end{pmatrix}{x}+...+{x}^{{a}−\mathrm{1}} \right\} \\ $$$${l}=\begin{pmatrix}{{a}}\\{\mathrm{1}}\end{pmatrix} \\ $$$${Now},\:{let}\:{a}=\mathrm{1}.\:\therefore\:{l}=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}=\mathrm{1}\:\Box \\ $$$$ \\ $$

Commented by Yozzi last updated on 03/Dec/15

Alternatively, consider the limit l=lim_(x→0) ((ln(x+1))/x). By the power rule of logarithms we obtain ((ln(1+x))/x)=ln(1+x)^(1/x) . ⇒l=lim_(x→0) ln(1+x)^(1/x) l=ln{lim_(x→0) (1+x)^(1/x) } Since e=lim_(x→0) (1+x)^(1/x) ⇒l=lne=1 Define L=lim_(x→0) ((e^x −1)/x) and let u=e^x −1. ∴ u→0⇔x→0. Also, x=ln(u+1). ∴ L=lim_(u→0) (u/(ln(u+1)))=(1/(lim_(x→0) ((ln(u+1))/u))) L=(1/1)=1 .

$${Alternatively},\:{consider}\:{the}\:{limit} \\ $$$${l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}\left({x}+\mathrm{1}\right)}{{x}}.\:\:{By}\:{the}\:{power}\:{rule} \\ $$$${of}\:{logarithms}\:{we}\:{obtain}\: \\ $$$$\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}={ln}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} . \\ $$$$\Rightarrow{l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{ln}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} \\ $$$${l}={ln}\left\{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} \right\} \\ $$$${Since}\:{e}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} \\ $$$$\Rightarrow{l}={lne}=\mathrm{1} \\ $$$${Define}\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}\:{and}\:{let}\:{u}={e}^{{x}} −\mathrm{1}. \\ $$$$\therefore\:{u}\rightarrow\mathrm{0}\Leftrightarrow{x}\rightarrow\mathrm{0}.\:\:{Also},\:{x}={ln}\left({u}+\mathrm{1}\right). \\ $$$$\therefore\:{L}=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}}{{ln}\left({u}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}\left({u}+\mathrm{1}\right)}{{u}}} \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1}\:. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 03/Dec/15

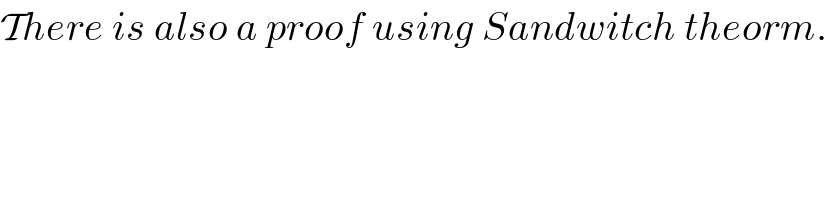
There is also a proof using Sandwitch theorm.

$$\mathcal{T}{here}\:{is}\:{also}\:{a}\:{proof}\:{using}\:{Sandwitch}\:{theorm}. \\ $$

Commented by Yozzi last updated on 03/Dec/15

Certainly.

$${Certainly}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com