Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 29855 by abdo imad last updated on 13/Feb/18

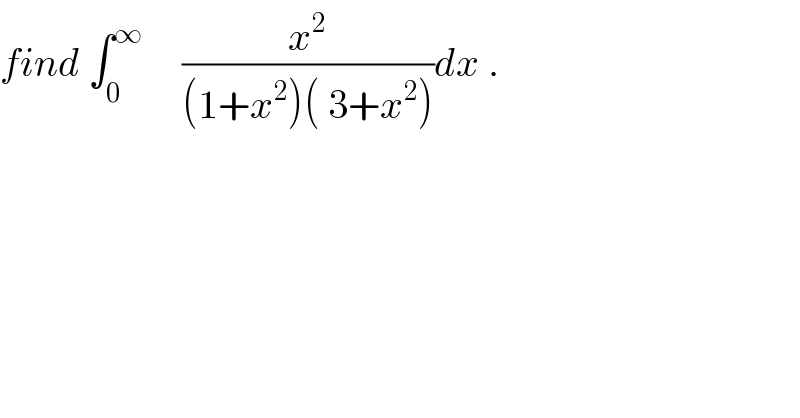
find ∫_0 ^∞ (x^2 /((1+x^2 )( 3+x^2 )))dx .

$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\:\mathrm{3}+{x}^{\mathrm{2}} \right)}{dx}\:. \\ $$

Commented by abdo imad last updated on 13/Feb/18

let put I= ∫_0 ^∞ (x^2 /((1+x^2 )(3+x^2 ))) I=(1/2) ∫_(−∞) ^(+∞) (x^2 /((1+x^2 )(3+x^2 ))) let introduce the complex function f(z)= (z^2 /((1+z^2 )(3+z^2 ))) the poles of f are i,−i (√3) i and−(√3) i and ∫_(−∞) ^(+∞) f(z)dz=2iπ( Res(f,i) +Res(f,i(√3))) Res(f,i)=lim_(z→i) (z−i)f(z)= ((−1)/((2i)(3−1)))=((−1)/(4i)) Res(f,i(√3))=lim_(z→i(√3)) (z−i(√3) )f(z)= ((−3)/(2i(√3)(−2)))=(3/(4i(√3))) ∫_(−∞) ^(+∞) f(z)dz=2iπ( ((−1)/(4i)) +(3/(4i(√3)))) =−(π/2) +((3π)/(2(√3))) =(π/2)( (√3) −1) ⇒ I = (π/4)((√3) −1) .

$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{3}+{x}^{\mathrm{2}} \right)} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{3}+{x}^{\mathrm{2}} \right)}\:{let}\:{introduce}\:{the}\:{complex} \\ $$$${function}\:{f}\left({z}\right)=\:\frac{{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{3}+{z}^{\mathrm{2}} \right)}\:{the}\:{poles}\:\:{of}\:{f}\:{are}\:{i},−{i} \\ $$$$\sqrt{\mathrm{3}}\:{i}\:{and}−\sqrt{\mathrm{3}}\:{i}\:\:{and} \\ $$$$\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}=\mathrm{2}{i}\pi\left(\:{Res}\left({f},{i}\right)\:+{Res}\left({f},{i}\sqrt{\mathrm{3}}\right)\right) \\ $$$${Res}\left({f},{i}\right)={lim}_{{z}\rightarrow{i}} \left({z}−{i}\right){f}\left({z}\right)=\:\:\frac{−\mathrm{1}}{\left(\mathrm{2}{i}\right)\left(\mathrm{3}−\mathrm{1}\right)}=\frac{−\mathrm{1}}{\mathrm{4}{i}} \\ $$$${Res}\left({f},{i}\sqrt{\mathrm{3}}\right)={lim}_{{z}\rightarrow{i}\sqrt{\mathrm{3}}} \left({z}−{i}\sqrt{\mathrm{3}}\:\right){f}\left({z}\right)=\:\frac{−\mathrm{3}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\left(−\mathrm{2}\right)}=\frac{\mathrm{3}}{\mathrm{4}{i}\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\:{f}\left({z}\right){dz}=\mathrm{2}{i}\pi\left(\:\frac{−\mathrm{1}}{\mathrm{4}{i}}\:+\frac{\mathrm{3}}{\mathrm{4}{i}\sqrt{\mathrm{3}}}\right)\:=−\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{3}\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\:\sqrt{\mathrm{3}}\:−\mathrm{1}\right)\:\:\Rightarrow\:\:{I}\:\:=\:\frac{\pi}{\mathrm{4}}\left(\sqrt{\mathrm{3}}\:−\mathrm{1}\right)\:. \\ $$

Answered by ajfour last updated on 13/Feb/18

= −(1/2)∫(dx/(1+x^2 )) +(3/2)∫(dx/(3+x^2 )) = −((tan^(−1) x)/2)+((√3)/2)tan^(−1) ((x/(√3)))+c . with limits 0 to ∞ I = −(π/4)+(((√3)π)/4) = ((((√3)−1)π)/4) .

$$\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\mathrm{3}+{x}^{\mathrm{2}} } \\ $$$$\:\:\:=\:−\frac{\mathrm{tan}^{−\mathrm{1}} {x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\sqrt{\mathrm{3}}}\right)+{c}\:. \\ $$$${with}\:{limits}\:\mathrm{0}\:{to}\:\infty \\ $$$$\:\:{I}\:=\:−\frac{\pi}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}\pi}{\mathrm{4}}\:\:=\:\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\pi}{\mathrm{4}}\:. \\ $$

Commented by abdo imad last updated on 14/Feb/18

yes correct thanks...

$${yes}\:{correct}\:{thanks}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com