Question Number 29896 by ajfour last updated on 13/Feb/18
Commented by ajfour last updated on 13/Feb/18
$${At}\:{least}\:{if}\:\alpha\:=\:\beta\:=\:\gamma\:=\theta\:\left({say}\right)\:. \\ $$
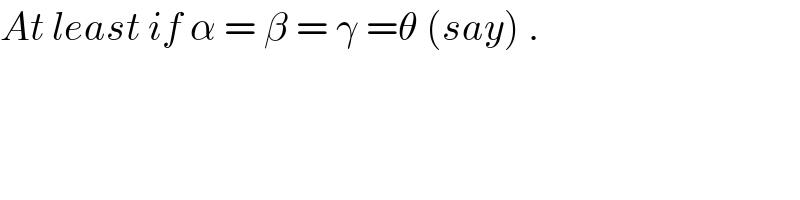
Answered by mrW2 last updated on 13/Feb/18
![take B as origin and BC as x−axis. B(0,0) C(a,0) A((a/2),(((√3)a)/2)) Eqn. of BE: y=tan α x Eqn. of CF: y=−tan ((π/3)−β) (x−a) Eqn. of AD: y=(((√3)a)/2)+tan ((π/3)+γ) (x−(a/2)) y_D =tan α x_D =(((√3)a)/2)+tan ((π/3)+γ) (x_D −(a/2)) [tan α−tan ((π/3)+γ)] x_D =(a/2)[(√3)−tan ((π/3)+γ)] ⇒x_D =((a[(√3)−tan ((π/3)+γ)])/(tan α−tan ((π/3)+γ))) ⇒y_D =((a[(√3)−tan ((π/3)+γ)]tan α)/(tan α−tan ((π/3)+γ))) y_E =tan α x_E =−tan ((π/3)−β) (x_E −a) (tan α+tan ((π/3)−β)] x_E =a tan ((π/3)−β) ⇒x_E =((a tan ((π/3)−β))/(tan α+tan ((π/3)−β))) ⇒y_E =((a tan ((π/3)−β) tan α)/(tan α+tan ((π/3)−β))) y_F =−tan ((π/3)−β) (x_F −a)=(((√3)a)/2)+tan ((π/3)+γ) (x_F −(a/2)) [tan ((π/3)+γ)+tan ((π/3)−β)] x_F =(a/2)[2tan ((π/3)−β)+tan ((π/3)+γ)−(√3)] ⇒x_F =((a[2tan ((π/3)−β)+tan ((π/3)+γ)−(√3)])/(2[tan ((π/3)+γ)+tan ((π/3)−β)])) ⇒y_F =((a[tan ((π/3)+γ)+(√3)]tan ((π/3)−β))/(2[tan ((π/3)+γ)+tan ((π/3)−β)])) A_(Blue) =(1/2)[x_D (y_E −y_F )+x_E (y_F −y_D )+x_F (y_D −y_E )] A_(Blue) =(a^2 /2)((((√3)−tan ((π/3)+γ))/(tan α−tan ((π/3)+γ)))×{((tan ((π/3)−β)tan α)/(tan α+tan ((π/3)−β)))−(([tan ((π/3)+γ)+(√3)]tan ((π/3)−β))/(2[tan ((π/3)+γ)+tan ((π/3)−β)]))}+((tan ((π/3)−β))/(tan α+tan ((π/3)−β)))×{(([tan ((π/3)+γ)+(√3)]tan ((π/3)−β))/(2[tan ((π/3)+γ)+tan ((π/3)−β)]))−(([(√3)−tan ((π/3)+γ)]tan α)/(tan α−tan ((π/3)+γ)))}+(([2tan ((π/3)−β)+tan ((π/3)+γ)−(√3)]tan α)/(2[tan ((π/3)+γ)+tan ((π/3)−β)]))×{(((√3)−tan ((π/3)+γ))/(tan α−tan ((π/3)+γ)))−((tan ((π/3)−β))/(tan α+tan ((π/3)−β)))})](Q29937.png)
$${take}\:{B}\:{as}\:{origin}\:{and}\:{BC}\:{as}\:{x}−{axis}. \\ $$$${B}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${C}\left({a},\mathrm{0}\right) \\ $$$${A}\left(\frac{{a}}{\mathrm{2}},\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${Eqn}.\:{of}\:{BE}: \\ $$$${y}=\mathrm{tan}\:\alpha\:{x} \\ $$$$ \\ $$$${Eqn}.\:{of}\:{CF}: \\ $$$${y}=−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\:\left({x}−{a}\right) \\ $$$$ \\ $$$${Eqn}.\:{of}\:{AD}: \\ $$$${y}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\:\left({x}−\frac{{a}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${y}_{{D}} =\mathrm{tan}\:\alpha\:{x}_{{D}} =\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\:\left({x}_{{D}} −\frac{{a}}{\mathrm{2}}\right) \\ $$$$\left[\mathrm{tan}\:\alpha−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\right]\:{x}_{{D}} =\frac{{a}}{\mathrm{2}}\left[\sqrt{\mathrm{3}}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\right] \\ $$$$\Rightarrow{x}_{{D}} =\frac{{a}\left[\sqrt{\mathrm{3}}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\right]}{\mathrm{tan}\:\alpha−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)} \\ $$$$\Rightarrow{y}_{{D}} =\frac{{a}\left[\sqrt{\mathrm{3}}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\right]\mathrm{tan}\:\alpha}{\mathrm{tan}\:\alpha−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)} \\ $$$$ \\ $$$${y}_{{E}} =\mathrm{tan}\:\alpha\:{x}_{{E}} =−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\:\left({x}_{{E}} −{a}\right) \\ $$$$\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]\:{x}_{{E}} ={a}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right) \\ $$$$\Rightarrow{x}_{{E}} =\frac{{a}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{tan}\:\alpha+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)} \\ $$$$\Rightarrow{y}_{{E}} =\frac{{a}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\:\mathrm{tan}\:\alpha}{\mathrm{tan}\:\alpha+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)} \\ $$$$ \\ $$$${y}_{{F}} =−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\:\left({x}_{{F}} −{a}\right)=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\:\left({x}_{{F}} −\frac{{a}}{\mathrm{2}}\right) \\ $$$$\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]\:{x}_{{F}} =\frac{{a}}{\mathrm{2}}\left[\mathrm{2tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)−\sqrt{\mathrm{3}}\right] \\ $$$$\Rightarrow{x}_{{F}} =\frac{{a}\left[\mathrm{2tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)−\sqrt{\mathrm{3}}\right]}{\mathrm{2}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]} \\ $$$$\Rightarrow{y}_{{F}} =\frac{{a}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\sqrt{\mathrm{3}}\right]\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{2}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]} \\ $$$$ \\ $$$${A}_{{Blue}} =\frac{\mathrm{1}}{\mathrm{2}}\left[{x}_{{D}} \left({y}_{{E}} −{y}_{{F}} \right)+{x}_{{E}} \left({y}_{{F}} −{y}_{{D}} \right)+{x}_{{F}} \left({y}_{{D}} −{y}_{{E}} \right)\right] \\ $$$$ \\ $$$${A}_{{Blue}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)}{\mathrm{tan}\:\alpha−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)}×\left\{\frac{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\mathrm{tan}\:\alpha}{\mathrm{tan}\:\alpha+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}−\frac{\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\sqrt{\mathrm{3}}\right]\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{2}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]}\right\}+\frac{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{tan}\:\alpha+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}×\left\{\frac{\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\sqrt{\mathrm{3}}\right]\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{2}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]}−\frac{\left[\sqrt{\mathrm{3}}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)\right]\mathrm{tan}\:\alpha}{\mathrm{tan}\:\alpha−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)}\right\}+\frac{\left[\mathrm{2tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)−\sqrt{\mathrm{3}}\right]\mathrm{tan}\:\alpha}{\mathrm{2}\left[\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\right]}×\left\{\frac{\sqrt{\mathrm{3}}−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)}{\mathrm{tan}\:\alpha−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right)}−\frac{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{tan}\:\alpha+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}\right\}\right) \\ $$
Commented by ajfour last updated on 14/Feb/18
$${Unlimited}\:{thanks}\:{Sir}. \\ $$$${I}\:{will}\:{try}\:{some}\:{vector}\:{approach}. \\ $$
Answered by ajfour last updated on 13/Feb/18
$${Area}\left(\bigtriangleup{DEF}\right)=\sqrt{\mathrm{3}}\:{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{6}}−\theta\right)\:. \\ $$
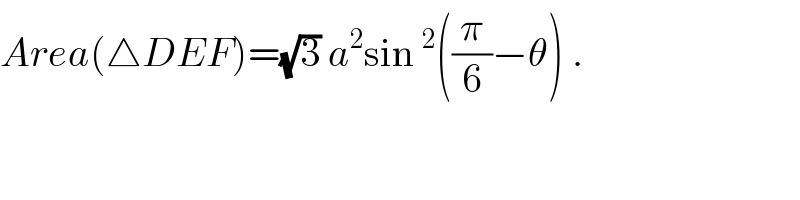
Answered by ajfour last updated on 14/Feb/18
![A=(a^2 /2)sin ((π/3)+α−β)[((sin (((2π)/3)+β))/(sin (((2π)/3)+β−α)))−((sin γ)/(sin ((π/3)+γ−α)))] ×[((sin (((2π)/3)+γ))/(sin ((π/3)+β−γ))) − ((sin α)/(sin (((2π)/3)+β−α)))] .](Q29991.png)
$${A}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha−\beta\right)\left[\frac{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right)}{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta−\alpha\right)}−\frac{\mathrm{sin}\:\gamma}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\gamma−\alpha\right)}\right] \\ $$$$\:\:\:\:\:\:×\left[\frac{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\gamma\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\beta−\gamma\right)}\:−\:\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta−\alpha\right)}\right]\:. \\ $$
Answered by ajfour last updated on 14/Feb/18
$${eq}.\:{of}\:{BDE}\:: \\ $$$${x}={p}\mathrm{cos}\:\alpha\:\:\:;\:\:{y}={p}\mathrm{sin}\:\alpha \\ $$$${eq}.\:{of}\:{CEF}\:: \\ $$$${x}={a}+{q}\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right)\:;\:{y}={q}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right) \\ $$$${eq}.\:{of}\:{AFD}\:: \\ $$$${x}=\frac{{a}}{\mathrm{2}}+{r}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right) \\ $$$${y}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right) \\ $$$${point}\:{E}\:\left({x}_{\mathrm{2}} ,\:{y}_{\mathrm{2}} \right)\:{lies}\:{on}\:{line}\:{BDE} \\ $$$${and}\:{line}\:{CEF}\:,\:{so} \\ $$$${p}_{\mathrm{2}} \mathrm{cos}\:\alpha={a}+{q}_{\mathrm{1}} \mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right) \\ $$$${p}_{\mathrm{2}} \mathrm{sin}\:\alpha={q}_{\mathrm{1}} \mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right) \\ $$$$\Rightarrow\:\:{p}_{\mathrm{2}} =\:\frac{{a}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right)}{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta−\alpha\right)} \\ $$$$\:\:\:\:\:{q}_{\mathrm{1}} =\:\frac{{a}\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta−\alpha\right)} \\ $$$$\:{point}\:{D}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:\:{lies}\:{on}\:{BDE}\: \\ $$$${and}\:{AFD},\:{so} \\ $$$${p}_{\mathrm{1}} \mathrm{cos}\:\alpha=\frac{{a}}{\mathrm{2}}+{r}_{\mathrm{2}} \mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right) \\ $$$${p}_{\mathrm{1}} \mathrm{sin}\:\alpha\:=\:\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}+{r}_{\mathrm{2}} \mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right) \\ $$$$\Rightarrow\:\:{p}_{\mathrm{1}} =\:\frac{{a}\mathrm{sin}\:\gamma}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\gamma−\alpha\right)} \\ $$$${point}\:{F}\:\left({x}_{\mathrm{3}} ,\:{y}_{\mathrm{3}} \right)\:{lies}\:{on}\:{CEF}\:{and} \\ $$$${AFD},\:{so} \\ $$$$\:{a}+{q}_{\mathrm{2}} \mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\beta\right)={r}_{\mathrm{1}} \mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right) \\ $$$${q}_{\mathrm{2}} \mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\beta\right)=\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}+{r}_{\mathrm{1}} \mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\gamma\right) \\ $$$$\Rightarrow\:\:\:{q}_{\mathrm{2}} =\frac{{a}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}+\gamma\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\beta−\gamma\right)} \\ $$$${A}=\:\frac{\mathrm{1}}{\mathrm{2}}\left({p}_{\mathrm{2}} −{p}_{\mathrm{1}} \right)\left({q}_{\mathrm{2}} −{q}_{\mathrm{1}} \right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha−\beta\right) \\ $$$${hence}\:{the}\:{answer}\:. \\ $$
Answered by mrW2 last updated on 14/Feb/18
![I have considered following method: ∠BEC=π−α−((π/3)−β)=π−((π/3)+α−β) ((BE)/(sin ((π/3)−β)))=((BC)/(sin [π−((π/3)+α−β)])) ⇒BE=((sin ((π/3)−β) a)/(sin ((π/3)−β+α))) A_(ΔBEC) =(a/2)×BE×sin α ⇒A_(ΔBEC) =(a^2 /2)×((sin α sin ((π/3)−β))/(sin ((π/3)−β+α))) ⇒A_(ΔCFA) =(a^2 /2)×((sin β sin ((π/3)−γ))/(sin ((π/3)−γ+β))) ⇒A_(ΔADB) =(a^2 /2)×((sin γ sin ((π/3)−α))/(sin ((π/3)−α+γ))) A_(ΔABC) =(a/2)×(((√3)a)/2)=(((√3)a^2 )/4) A_(Blue) =A_(ΔABC) −A_(ΔBEC) −A_(ΔCFA) −A_(ΔADB) ⇒A_(Blue) =(a^2 /2)[((√3)/2)−Σ((sin α sin ((π/3)−β))/(sin ((π/3)−β+α)))] ⇒A_(Blue) =(a^2 /2)[((√3)/2)−((sin α sin ((π/3)−β))/(sin ((π/3)−β+α)))−((sin β sin ((π/3)−γ))/(sin ((π/3)−γ+β)))−((sin γ sin ((π/3)−α))/(sin ((π/3)−α+γ)))] if α=β=γ=θ: ⇒A_(Blue) =(a^2 /2)[((√3)/2)−3((sin θ sin ((π/3)−θ))/(sin ((π/3))))] =(a^2 /2)[((√3)/2)−(√3) sin θ ((√3) cos θ−sin θ)] =(a^2 /2)[((√3)/2)−(3/2) sin 2θ +((√3)/2) (1−cos 2θ)] =(a^2 /2)[(√3)−(√3)(sin (π/3) sin 2θ +cos (π/3) cos 2θ)] ⇒A_(Blue) =(((√3)a^2 )/2)[1− cos ((π/3)−2θ)] or ⇒A_(Blue) =(√3)a^2 sin^2 ((π/6)−θ)](Q30004.png)
$${I}\:{have}\:{considered}\:{following}\:{method}: \\ $$$$\angle{BEC}=\pi−\alpha−\left(\frac{\pi}{\mathrm{3}}−\beta\right)=\pi−\left(\frac{\pi}{\mathrm{3}}+\alpha−\beta\right) \\ $$$$\frac{{BE}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}=\frac{{BC}}{\mathrm{sin}\:\left[\pi−\left(\frac{\pi}{\mathrm{3}}+\alpha−\beta\right)\right]} \\ $$$$\Rightarrow{BE}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)\:{a}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta+\alpha\right)} \\ $$$${A}_{\Delta{BEC}} =\frac{{a}}{\mathrm{2}}×{BE}×\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{A}_{\Delta{BEC}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta+\alpha\right)} \\ $$$$\Rightarrow{A}_{\Delta{CFA}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{sin}\:\beta\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\gamma\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\gamma+\beta\right)} \\ $$$$\Rightarrow{A}_{\Delta{ADB}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{sin}\:\gamma\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha+\gamma\right)} \\ $$$${A}_{\Delta{ABC}} =\frac{{a}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$$${A}_{{Blue}} ={A}_{\Delta{ABC}} −{A}_{\Delta{BEC}} −{A}_{\Delta{CFA}} −{A}_{\Delta{ADB}} \\ $$$$\Rightarrow{A}_{{Blue}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\Sigma\frac{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta+\alpha\right)}\right] \\ $$$$\Rightarrow{A}_{{Blue}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta+\alpha\right)}−\frac{\mathrm{sin}\:\beta\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\gamma\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\gamma+\beta\right)}−\frac{\mathrm{sin}\:\gamma\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha+\gamma\right)}\right] \\ $$$$ \\ $$$${if}\:\alpha=\beta=\gamma=\theta: \\ $$$$\Rightarrow{A}_{{Blue}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{3}\frac{\mathrm{sin}\:\theta\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\theta\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}\right)}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\:\left(\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\sqrt{\mathrm{3}}−\sqrt{\mathrm{3}}\left(\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\:\mathrm{sin}\:\mathrm{2}\theta\:+\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:\mathrm{cos}\:\mathrm{2}\theta\right)\right] \\ $$$$\Rightarrow{A}_{{Blue}} =\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{1}−\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{2}\theta\right)\right] \\ $$$${or} \\ $$$$\Rightarrow{A}_{{Blue}} =\sqrt{\mathrm{3}}{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{6}}−\theta\right) \\ $$
Commented by ajfour last updated on 14/Feb/18
$${Much}\:{better},\:{Indeed}\:!\:{Sir}. \\ $$
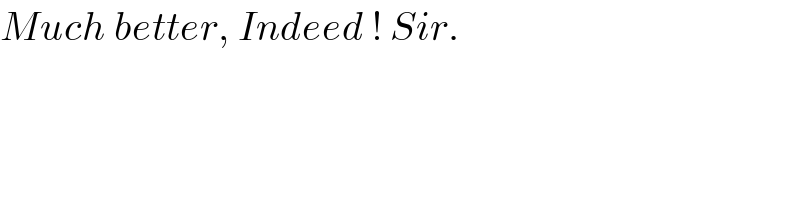
Commented by mrW2 last updated on 15/Feb/18
![Using this method we can also find A_(Blue) in an arbitrary triangle with side lengths a,b,c: A_(Blue) =(1/4)(√((a+b+c)(a+b−c)(a−b+c)(−a+b+c)))−(1/2)[((a^2 sin α sin ((π/3)−β))/(sin ((π/3)−β+α)))+((b^(2 ) sin β sin ((π/3)−γ))/(sin ((π/3)−γ+β)))+((c^2 sin γ sin ((π/3)−α))/(sin ((π/3)−α+γ)))]](Q30073.png)
$${Using}\:{this}\:{method}\:{we}\:{can}\:{also}\:{find} \\ $$$${A}_{{Blue}} \:{in}\:{an}\:{arbitrary}\:{triangle}\:{with}\:{side} \\ $$$${lengths}\:{a},{b},{c}: \\ $$$${A}_{{Blue}} =\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}−{b}+{c}\right)\left(−{a}+{b}+{c}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{a}^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\beta+\alpha\right)}+\frac{{b}^{\mathrm{2}\:} \mathrm{sin}\:\beta\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\gamma\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\gamma+\beta\right)}+\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\gamma\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha+\gamma\right)}\right] \\ $$
Commented by ajfour last updated on 16/Feb/18
$${Thank}\:{you}\:{Sir}.\: \\ $$$$\left({conclusion}:\:{Area}\:{is}\:{easily}\:{obtained}\:\right. \\ $$$$\left.{from}\:{areas}.\right) \\ $$