
Question and Answers Forum
Question Number 29971 by abdo imad last updated on 14/Feb/18
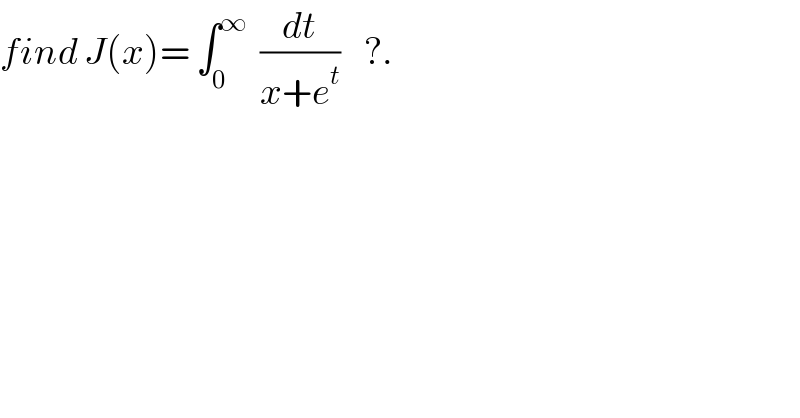
Commented by abdo imad last updated on 16/Feb/18
![J(x)= ∫_0 ^∞ (dt/(e^t ( 1+x e^(−t) ))) =∫_0 ^∞ e^(−t) (Σ_(n=0) ^∞ x^n e^(−nt) )dt = Σ_(n=0) ^∞ x^n ∫_0 ^∞ e^(−(n+1)t) dt the (n+1)t=u give ∫_0 ^∞ e^(−(n+1)t) dt= ∫_0 ^∞ e^(−u) (du/(n+1)) =(1/(n+1)) [−e^(−u) ]_0 ^(+∞) =(1/(n+1)) J(x)= Σ_(n=0) ^∞ (x^n /(n+1)) ⇒ x J(x)=Σ_(n=0) ^∞ (x^(n+1) /(n+1)) let derivate J(x) +xJ^′ (x)= Σ_(n=0) ^∞ x^n = (1/(1−x)) so J is solution of the d.e y +xy^′ =(1/(1−x)) eh⇒ xy^′ =−y ⇒(y^′ /y) =((−1)/x) ⇒ ln∣y∣= −ln∣x∣+c ⇒y= (λ/x) mvc method give y^′ =((λ^′ x −λ)/x^2 ) ⇒(λ/x) +λ^′ −(λ/x) = (1/(1−x)) ⇒λ(x)=∫ (dx/(1−x)) +κ =−ln∣1−x∣ +k but k=λ(0)=0 y(x)=−(1/x)ln∣1−x∣ ⇒ J(x)=−(1/x)ln∣1−x∣ .](Q30110.png)
Commented by abdo imad last updated on 16/Feb/18
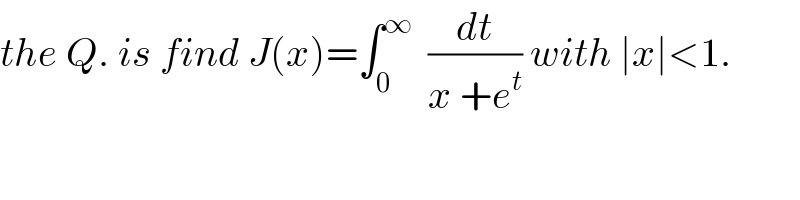
| ||
Question and Answers Forum | ||
Question Number 29971 by abdo imad last updated on 14/Feb/18 | ||
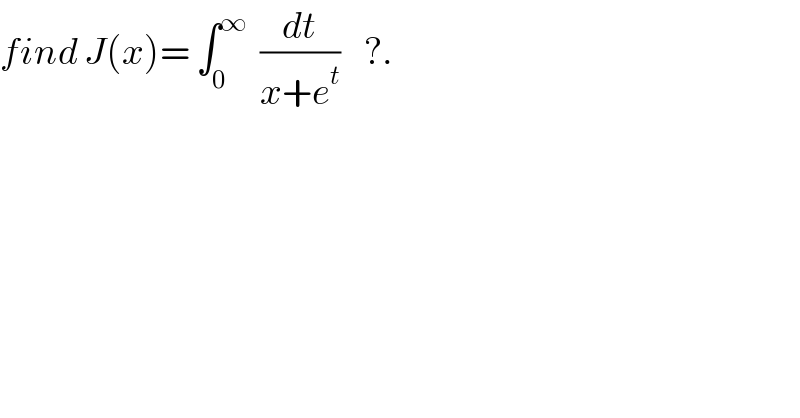 | ||
Commented by abdo imad last updated on 16/Feb/18 | ||
![J(x)= ∫_0 ^∞ (dt/(e^t ( 1+x e^(−t) ))) =∫_0 ^∞ e^(−t) (Σ_(n=0) ^∞ x^n e^(−nt) )dt = Σ_(n=0) ^∞ x^n ∫_0 ^∞ e^(−(n+1)t) dt the (n+1)t=u give ∫_0 ^∞ e^(−(n+1)t) dt= ∫_0 ^∞ e^(−u) (du/(n+1)) =(1/(n+1)) [−e^(−u) ]_0 ^(+∞) =(1/(n+1)) J(x)= Σ_(n=0) ^∞ (x^n /(n+1)) ⇒ x J(x)=Σ_(n=0) ^∞ (x^(n+1) /(n+1)) let derivate J(x) +xJ^′ (x)= Σ_(n=0) ^∞ x^n = (1/(1−x)) so J is solution of the d.e y +xy^′ =(1/(1−x)) eh⇒ xy^′ =−y ⇒(y^′ /y) =((−1)/x) ⇒ ln∣y∣= −ln∣x∣+c ⇒y= (λ/x) mvc method give y^′ =((λ^′ x −λ)/x^2 ) ⇒(λ/x) +λ^′ −(λ/x) = (1/(1−x)) ⇒λ(x)=∫ (dx/(1−x)) +κ =−ln∣1−x∣ +k but k=λ(0)=0 y(x)=−(1/x)ln∣1−x∣ ⇒ J(x)=−(1/x)ln∣1−x∣ .](Q30110.png) | ||
Commented by abdo imad last updated on 16/Feb/18 | ||
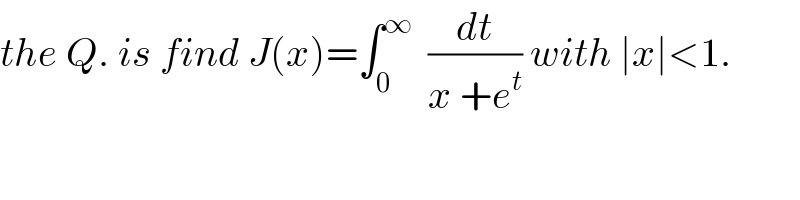 | ||