Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 29972 by abdo imad last updated on 14/Feb/18

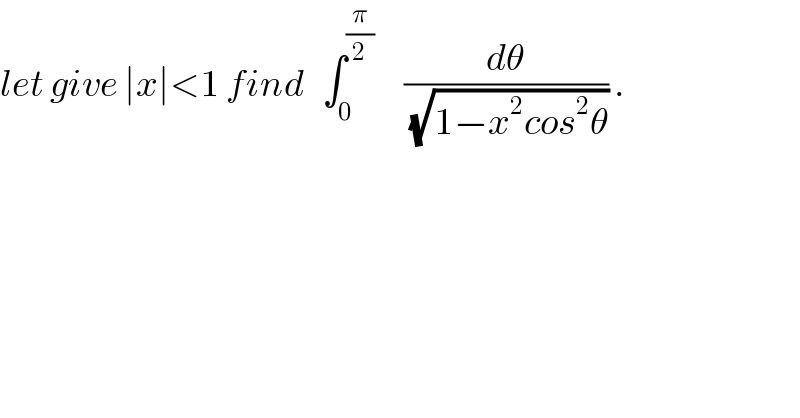
let give ∣x∣<1 find ∫_0 ^(π/2) (dθ/(√(1−x^2 cos^2 θ))) .

$${let}\:{give}\:\mid{x}\mid<\mathrm{1}\:{find}\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{d}\theta}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}}\:. \\ $$

Commented byabdo imad last updated on 18/Feb/18

we have (1+u^ )^α =1+αu +((α(α−1))/(2!))u^2 +... =1+Σ_(n=1) ^∞ ((α(α−1)...(α−n+1))/(n!))u^n with∣u∣<1 we have ∣xcosθ∣<1 ⇒ (1/(√(1−x^2 cos^2 θ)))=(1−(xcosθ)^2 )^(−(1/2)) =1+Σ_(n=1) ^∞ (((−(1/2))(−(1/2)−1)...(−(1/2)−n+1))/(n!)) x^(2n) cos^(2n) θ let put A_n =(−(1/2))(−(1/2)−1)...(−(1/2)−n+1) ⇒ ∫_0 ^(π/2) (dθ/(√(1−x^2 cos^2 θ)))=(π/2) +Σ_(n=1) ^∞ (A_n /(n!))x^(2n) ∫_0 ^(π/2) cos^(2n) θ dθ but w_n =∫_0 ^(π/2) cos^(2n) θdθ is known (wallis integral) so ∫_0 ^(π/2) (dθ/(√(1−x^2 cos^2 θ))) = (π/2) +Σ_(n=1) ^∞ ((A_n B_n )/(n!)) x^(2n) .

$${we}\:{have}\:\left(\mathrm{1}+{u}^{} \right)^{\alpha} \:\:=\mathrm{1}+\alpha{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}{u}^{\mathrm{2}} \:+... \\ $$ $$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\alpha\left(\alpha−\mathrm{1}\right)...\left(\alpha−{n}+\mathrm{1}\right)}{{n}!}{u}^{{n}} \:\:\:{with}\mid{u}\mid<\mathrm{1}\:{we}\:{have} \\ $$ $$\mid{xcos}\theta\mid<\mathrm{1}\:\Rightarrow\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}}=\left(\mathrm{1}−\left({xcos}\theta\right)^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$ $$=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)...\left(−\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)}{{n}!}\:{x}^{\mathrm{2}{n}} \:{cos}^{\mathrm{2}{n}} \theta\:{let} \\ $$ $${put}\:{A}_{{n}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)...\left(−\frac{\mathrm{1}}{\mathrm{2}}−{n}+\mathrm{1}\right)\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{d}\theta}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}}=\frac{\pi}{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{A}_{{n}} }{{n}!}{x}^{\mathrm{2}{n}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}} \theta\:{d}\theta\:{but} \\ $$ $${w}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}} \theta{d}\theta\:{is}\:{known}\:\left({wallis}\:{integral}\right)\:{so} \\ $$ $$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} \:{cos}^{\mathrm{2}} \theta}}\:=\:\frac{\pi}{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{A}_{{n}} \:{B}_{{n}} }{{n}!}\:{x}^{\mathrm{2}{n}} \:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com