
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 29978 by abdo imad last updated on 14/Feb/18
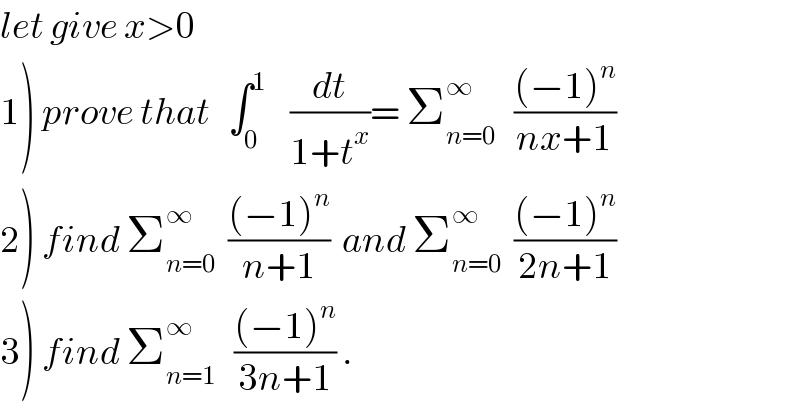
Commented byabdo imad last updated on 16/Feb/18
![1) for t∈]0,1] t^x =e^(xlnt) <1 ⇒ ∫_0 ^1 (dt/(1+t^x ))=∫_0 ^1 (Σ_(n=0) ^∞ (−1)^n t^(nx) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 t^(nx) dt=Σ_(n=0) ^∞ (((−1)^n )/(nx +1)) 2) we have proved that A(x)=Σ_(n=0) ^∞ (((−1)^n )/(nx+1))=∫_0 ^1 (dt/(1+t^x ))⇒ Σ_(n=0) ^∞ (((−1)^n )/(n+1))=A(1)=∫_0 ^1 (dt/(1+t))=[ln(1+t)]_0 ^1 =ln(2) Σ_(n=0) ^∞ (((−1)^n )/(2n+1))=A(2)=∫_0 ^1 (dt/(1+t^2 ))=[arctant]_0 ^1 =(π/4) 3)we have Σ_(n=0) ^∞ (((−1)^n )/(3n+1))= A(3) = ∫_0 ^1 (dt/(1+t^3 )) we have ∫_0 ^∞ (dt/(1+t^3 )) = ∫_0 ^1 (dt/(1+t^3 )) +∫_1 ^(+∞) (dt/(1+t^3 )) the ch. t=(1/u) give ∫_1 ^∞ (dt/(1+t^3 ))=∫_0 ^1 (1/(1+(1/u^3 ))) (du/u^2 )= ∫_0 ^1 (du/(u^2 +(1/u))) =∫_0 ^1 ((udu)/(1+u^2 )) =(1/2)[ln(1+u^2 )]_0 ^1 =(1/2)ln2 the ch. t^3 =u give ∫_0 ^∞ (dt/(1+t^3 )) = ∫_0 ^∞ (1/(1+u))(1/3)u^((1/3)−1) du =(1/3)∫_0 ^∞ (u^((1/3)−1) /(1+u))du =(1/3) (π/(sin((π/3))))=(π/3) (1/((√3)/2)) =((2π)/(3(√3))) ⇒ ∫_0 ^1 (dt/(1+t^3 )) =∫_0 ^∞ (dt/(1+t^3 )) − ∫_1 ^(+∞) (dt/(1+t^3 ))=((2π)/(3(√3))) −(1/2)ln(2)⇒ Σ_(n=0) ^∞ (((−1)^n )/(3n+1))=((2π)/(3(√3))) −(1/2)ln(2).](Q30074.png)
Commented byabdo imad last updated on 16/Feb/18
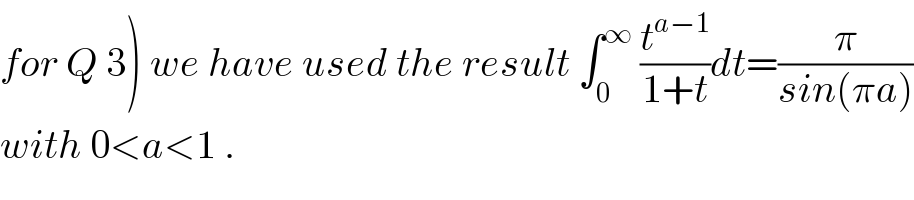
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 29978 by abdo imad last updated on 14/Feb/18 | ||
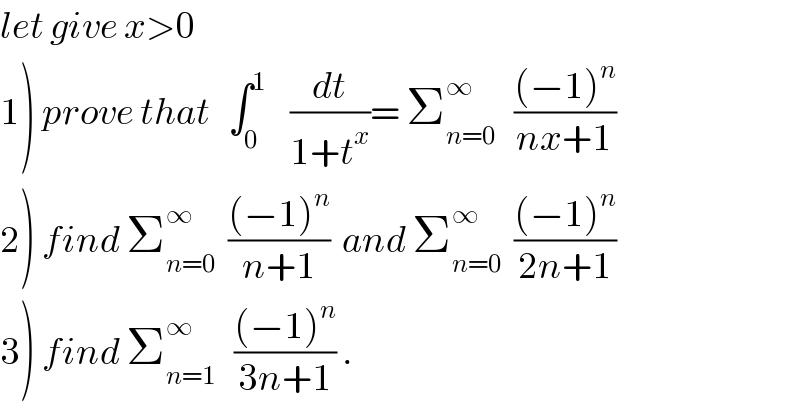 | ||
Commented byabdo imad last updated on 16/Feb/18 | ||
![1) for t∈]0,1] t^x =e^(xlnt) <1 ⇒ ∫_0 ^1 (dt/(1+t^x ))=∫_0 ^1 (Σ_(n=0) ^∞ (−1)^n t^(nx) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 t^(nx) dt=Σ_(n=0) ^∞ (((−1)^n )/(nx +1)) 2) we have proved that A(x)=Σ_(n=0) ^∞ (((−1)^n )/(nx+1))=∫_0 ^1 (dt/(1+t^x ))⇒ Σ_(n=0) ^∞ (((−1)^n )/(n+1))=A(1)=∫_0 ^1 (dt/(1+t))=[ln(1+t)]_0 ^1 =ln(2) Σ_(n=0) ^∞ (((−1)^n )/(2n+1))=A(2)=∫_0 ^1 (dt/(1+t^2 ))=[arctant]_0 ^1 =(π/4) 3)we have Σ_(n=0) ^∞ (((−1)^n )/(3n+1))= A(3) = ∫_0 ^1 (dt/(1+t^3 )) we have ∫_0 ^∞ (dt/(1+t^3 )) = ∫_0 ^1 (dt/(1+t^3 )) +∫_1 ^(+∞) (dt/(1+t^3 )) the ch. t=(1/u) give ∫_1 ^∞ (dt/(1+t^3 ))=∫_0 ^1 (1/(1+(1/u^3 ))) (du/u^2 )= ∫_0 ^1 (du/(u^2 +(1/u))) =∫_0 ^1 ((udu)/(1+u^2 )) =(1/2)[ln(1+u^2 )]_0 ^1 =(1/2)ln2 the ch. t^3 =u give ∫_0 ^∞ (dt/(1+t^3 )) = ∫_0 ^∞ (1/(1+u))(1/3)u^((1/3)−1) du =(1/3)∫_0 ^∞ (u^((1/3)−1) /(1+u))du =(1/3) (π/(sin((π/3))))=(π/3) (1/((√3)/2)) =((2π)/(3(√3))) ⇒ ∫_0 ^1 (dt/(1+t^3 )) =∫_0 ^∞ (dt/(1+t^3 )) − ∫_1 ^(+∞) (dt/(1+t^3 ))=((2π)/(3(√3))) −(1/2)ln(2)⇒ Σ_(n=0) ^∞ (((−1)^n )/(3n+1))=((2π)/(3(√3))) −(1/2)ln(2).](Q30074.png) | ||
Commented byabdo imad last updated on 16/Feb/18 | ||
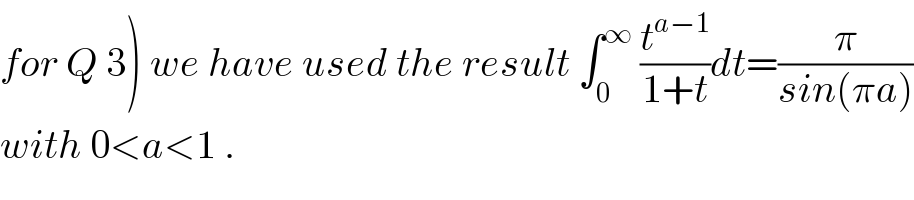 | ||